设计转子侧变换器的模糊控制器

2023-06-23 理论教育版权反馈

【摘要】：近年来模糊控制已被应用于电力电子系统，包括电机的速度控制、变流器的反馈控制、在线和离线诊断、参数估计等，本书尝试将模糊控制应用于双馈发电机的控制，只对转速环节设计二维模糊控制器，并进行必要的仿真分析。模糊控制中采用单位变量的好处在于同样的控制算法能被应用到同类性质的所有被控对象中，这使得模糊控制器的设计更为方便。表5-1给出了转速模糊控制器中对应的规则表。表4-1 用于转速模糊控制的规则矩阵

双馈发电机的动态d-q模型是一个非线性、多扰动、多变量、高阶次的时变系统，对其进行精确控制较为困难，而模糊控制具有非线性和自适应控制规律，对参数变化的线性或非线性对象有很强的鲁棒性。它的控制规则只用逻辑语言变量的形式定性表示，即可建立被控对象的模糊模型，特别适用于不易获得精确数学模型的被控对象。

模糊集合理论在1965年由美国教授Zandeh提出，由此开创了模糊数学及其应用的新纪元。模糊控制是模糊集合理论应用的一个重要方面。1974年英国教授Mamdani首先将模糊集合理论应用于锅炉和蒸汽机的动态过程控制，这些研究具有重要意义，激发了模糊控制领域的研究热潮。近年来模糊控制已被应用于电力电子系统，包括电机的速度控制、变流器的反馈控制、在线和离线诊断、参数估计等，本书尝试将模糊控制应用于双馈发电机的控制，只对转速环节设计二维模糊控制器，并进行必要的仿真分析。

图4-7为一般情况下矢量控制系统中的模糊速度控制器模块。该控制器根据速度误差信号更新输出DU，以使实际速度ω_r跟踪上给定速度ω_r^*。模糊控制器有两个输入信号，即偏差E和偏差变化量CE（与偏差的导数有关）。在矢量控制系统中，控制器输出量DU是转矩电流增量Δi_qr^*，它的和或积分产生实际的控制信号U或转矩电流给定量i_qr^*。结合风力发电系统中转速环节控制原理，可以建立如图4-8所示的基于转速模糊逻辑控制的双馈发电机发电运行控制框图。

可将该模糊控制器看成一个输入/输出的静态非线性映射，因此可用如下形式描述其控制作用：

K₁E+K₂CE=DU （4-22）

式中，K₁和K₂为非线性系数或增益因数，考虑到图4-7中的求和或积分过程，可以得到

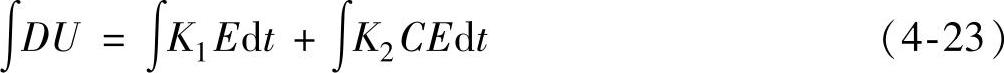
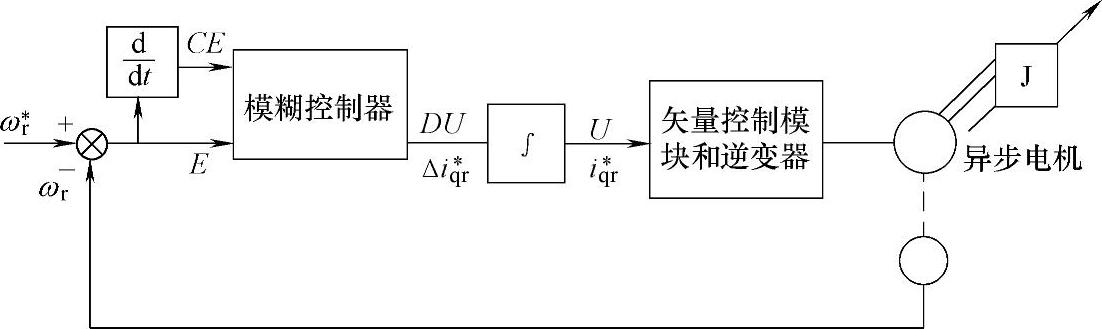
图4-7 矢量控制系统中的模糊控制器模块

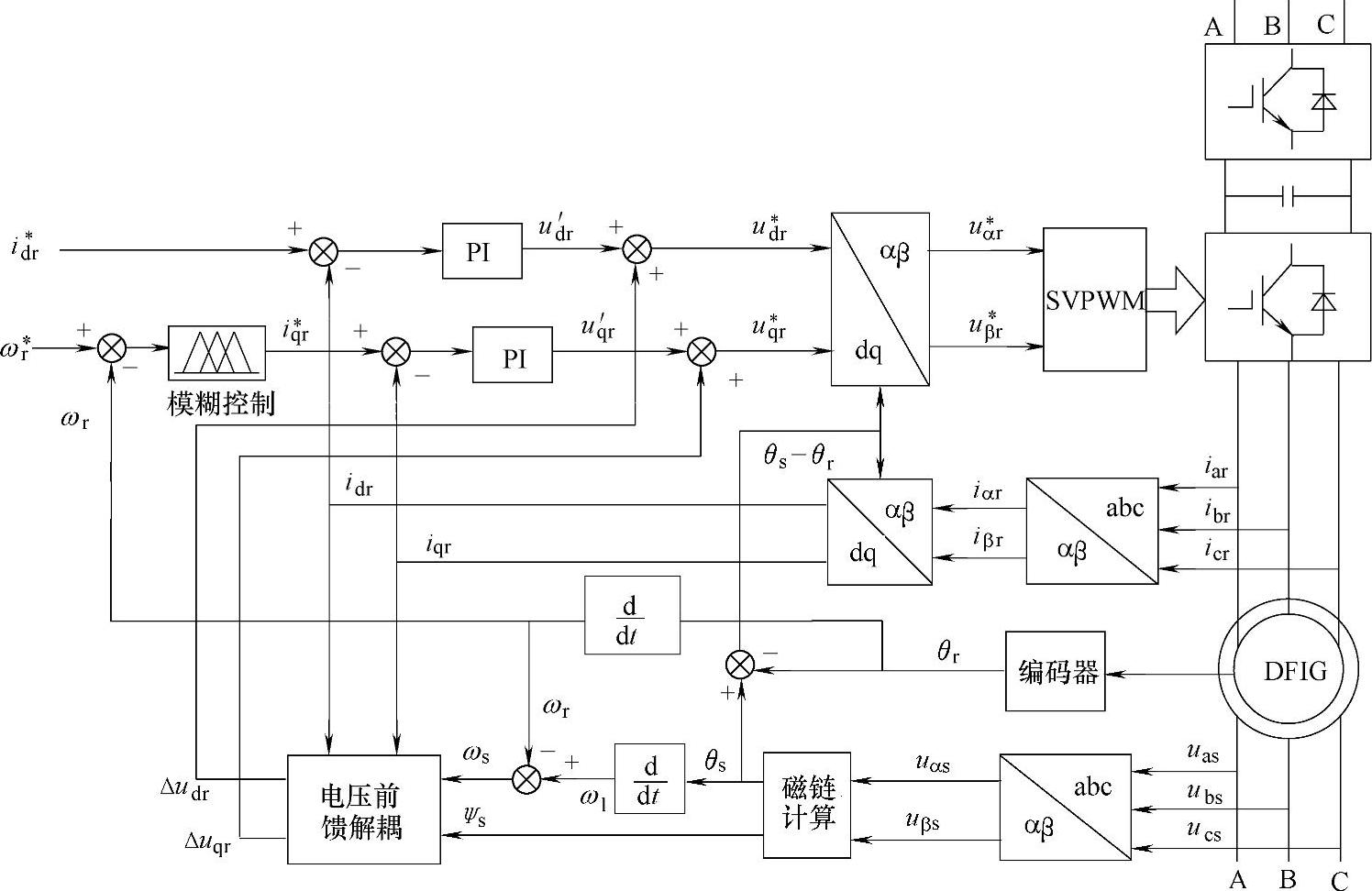
图4-8 基于转速模糊控制的双馈发电机发电运行控制框图

或者

可见这是一种含有非线性增益因数的模糊PI控制器。模糊控制器在线变化的非线性自适应增益使得它的控制系统响应对参数变化和负载干扰具有鲁棒性。

典型反馈系统中的模糊控制结构如图4-9所示。闭环偏差和偏差变化量通过除以各自的量化因子，被转化为对应的单位信号e和ce。输出控制信号由量化因子GU和单位输出相乘得到，然后对其求和得到实际的控制信号U。模糊控制中采用单位变量的好处在于同样的控制算法能被应用到同类性质的所有被控对象中，这使得模糊控制器的设计更为方便。量化因子可以是常数也可以是可编程的，可编程的量化因子可用来调节不同控制区域的灵敏度，或使同样的控制策略可应用到相似的反馈闭环系统中。

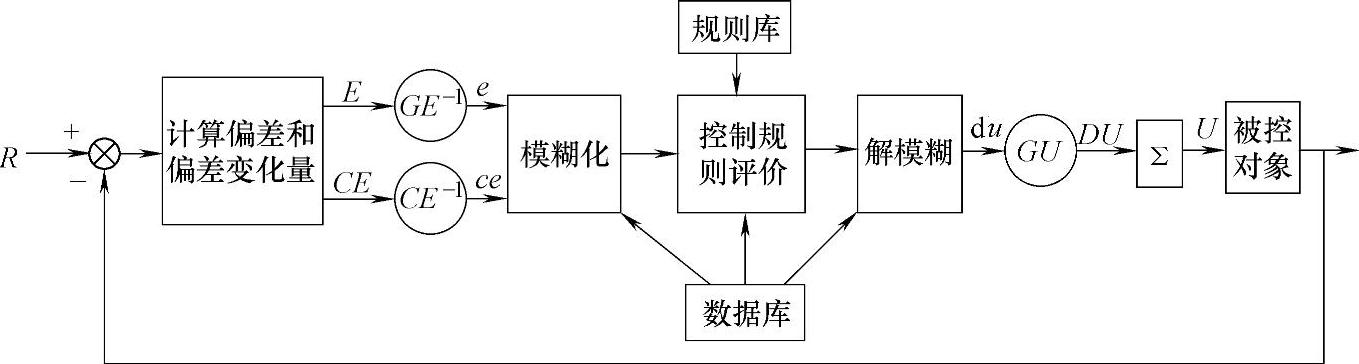
图4-9 典型反馈系统中的模糊控制结构

对于图4-9所示的模糊转速控制系统，其输入信号为E和CE，输出信号为DU，各信号的模糊集及其对应的三角形隶属函数分布如图4-10所示。定义模糊集合如下：Z=零，PS=正小，PM=正中，PB=正大，NS=负小，NM=负中，NB=负大，PVS=正非常小，NVS=负非常小。涵盖整个区间的各变量论域用单位值表示。信号e（pu）和ce（pu）有7个MF（隶属度函数），因为在原点处（稳态点）附近要求信号更加精确，输出设定有9个MF，所有MF在变量的正负半轴是对称的。模糊控制规则库由一系列“IF-AND-THEN”型模糊逻辑条件语句构成。表5-1给出了转速模糊控制器中对应的规则表。规则矩阵的第一行和左数第一列表示输入变量E和CE的模糊集合，矩阵主体元素表示输出变量DU的MF。规则库共包含7×7=49条规则。

在模糊控制器的设计中，一般有如下规则：①如果e（pu）和ce（pu）都为零，那么保持目前的控制量，令du（pu）=0；②如果e（pu）非零，但却以理想的速度接近零，那么保持目前的控制量；③如果e（pu）增长，那么根据信号e（pu）和ce（pu）的大小改变控制信号du（pu）使e（pu）趋于零。

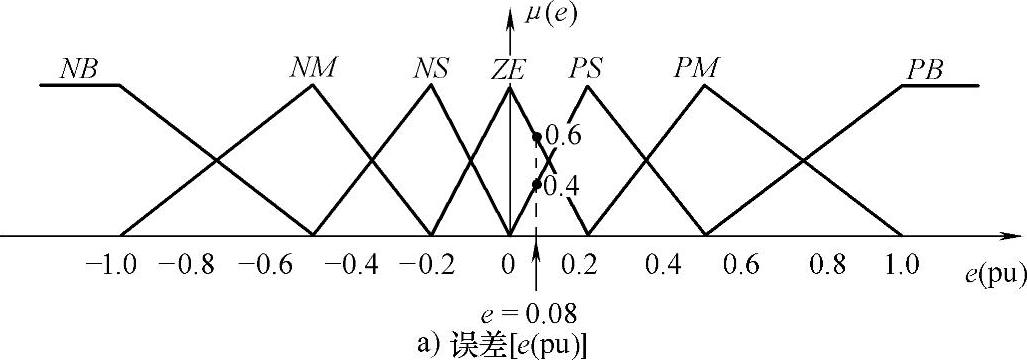
图4-10 转速模糊控制的隶属函数

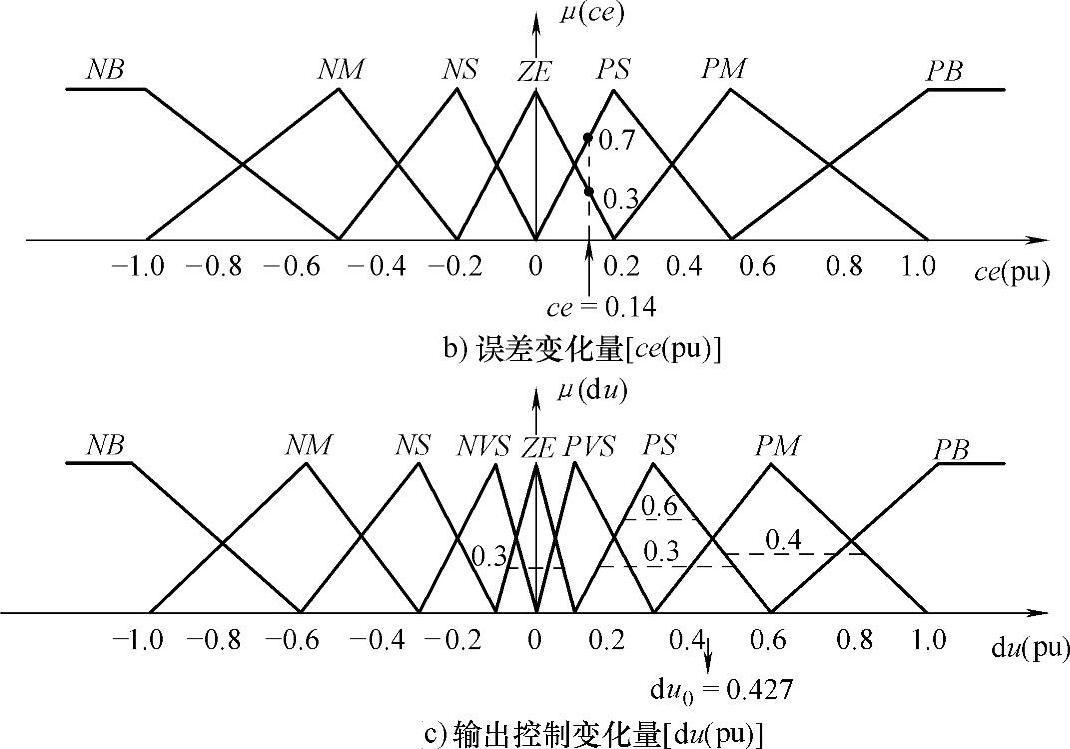
图4-10 转速模糊控制的隶属函数（续）

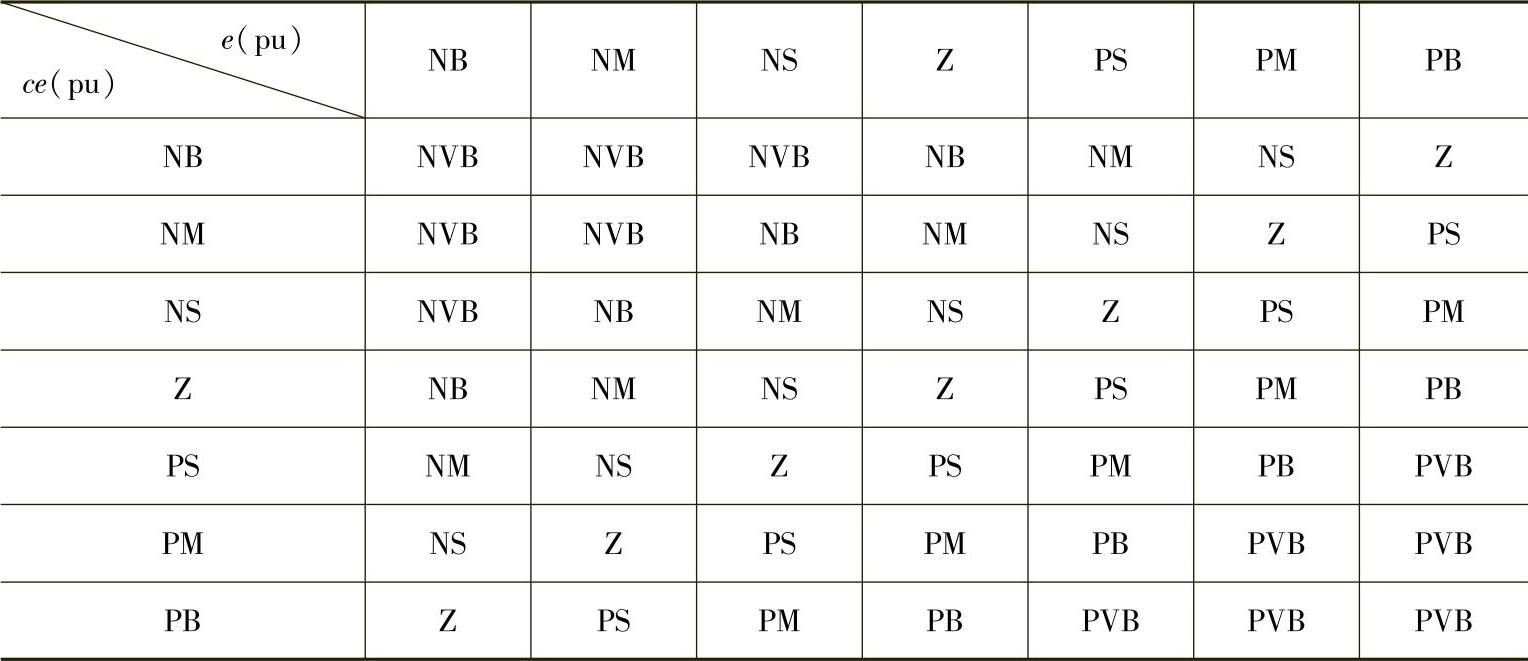
用于转速模糊控制的规则矩阵见表4-1。

表4-1 用于转速模糊控制的规则矩阵

设计转子侧变换器的模糊控制器

相关推荐