【摘要】:内模控制在双馈风力发电系统转子电流环的控制框图如图4-3所示。图4-3 内模控制原理图其中,CIMC为内模控制器,G为被控对象,iref为控制系统输入,i为控制系统输出,为被控对象的内模,F为虚线框内的等效传递函数。从而内模控制器就变为常规PI控制器,且当取R=αLr-Rr时,即有kP=αLr,kI=α2Lr=αkP。
内模控制在双馈风力发电系统转子电流环的控制框图如图4-3所示。
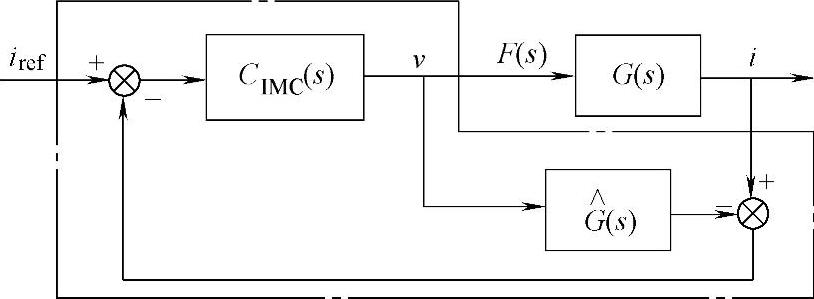
图4-3 内模控制原理图
其中,CIMC(s)为内模控制器,G(s)为被控对象,iref为控制系统输入,i为控制系统输出, 为被控对象的内模,F(s)为虚线框内的等效传递函数。内模控制的基本原理是在控制系统中引入内部模型,将反馈量变为扰动估计量的反馈,使控制器设计变得简单,当模型不能准确描述对象时,反馈量还将包含模型失配信息,有助于提高系统鲁棒性,该控制器的设计主要是选取适当的传递函数CIMC(s)。
为被控对象的内模,F(s)为虚线框内的等效传递函数。内模控制的基本原理是在控制系统中引入内部模型,将反馈量变为扰动估计量的反馈,使控制器设计变得简单,当模型不能准确描述对象时,反馈量还将包含模型失配信息,有助于提高系统鲁棒性,该控制器的设计主要是选取适当的传递函数CIMC(s)。
普遍的工程设计方法就是令
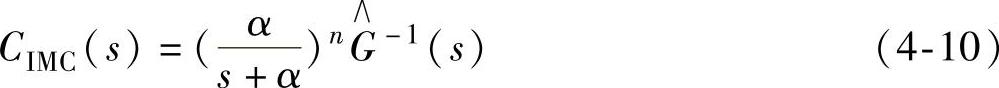
选择适当的n可使传递函数中分母的最高阶数大于分子的最高阶数。α为带宽,是IMC的主要设计参数,其值为 ,trise为系统上升时间。该闭环系统的传递函数为
,trise为系统上升时间。该闭环系统的传递函数为
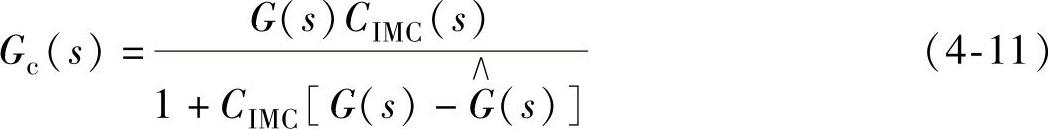
当 时,上式简化为
时,上式简化为
同理,可求得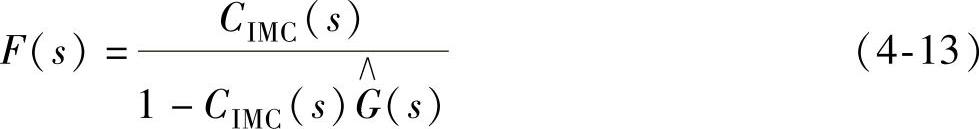
但是据此设计的IMC存在闭环动态响应慢、对干扰不能有效抑制的缺点,为了解决这一问题,可在该系统中附加一前馈环节,提高系统抗扰性能,改进的内模控制框图如图4-4所示。此时干扰传递函数为
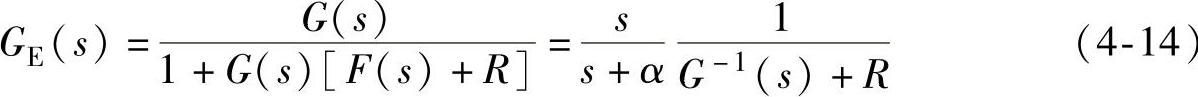
对于一阶系统,只要选取适当的R,本文取R=αLr-Rr,上面的干扰传递函数就可以变为
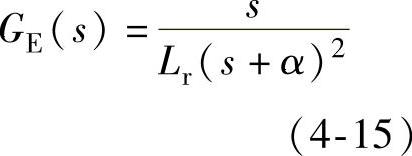
从而对扰动实现削弱作用。应用双馈发电机理论可知,增加前馈环节后转子电流环节传递函数
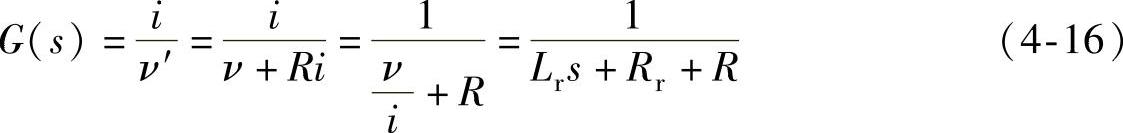
为一阶系统,n设置为1就可以实现系统预期控制目标。从而内模控制器就变为常规PI控制器,且
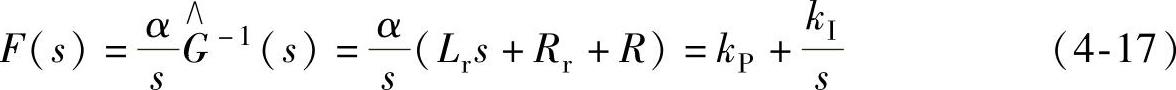
当取R=αLr-Rr时,即有kP=αLr,kI=α2Lr=αkP。
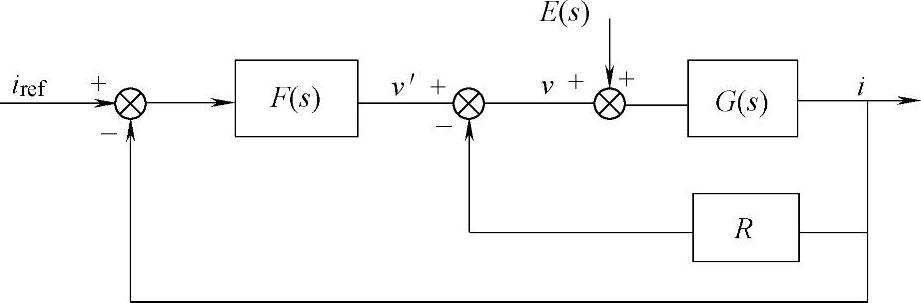
图4-4 改进的内模控制框图


 为被控对象的内模,
为被控对象的内模,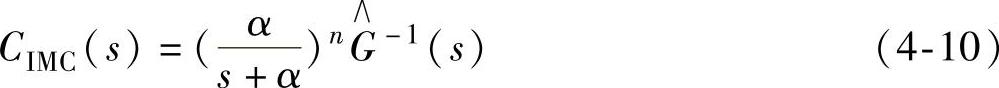
 ,
,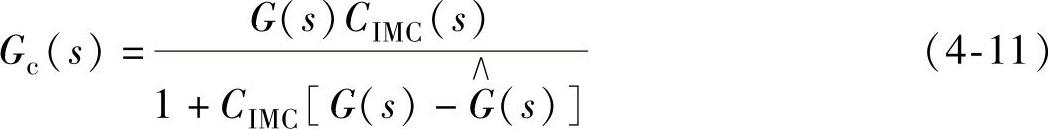
 时,上式简化为
时,上式简化为
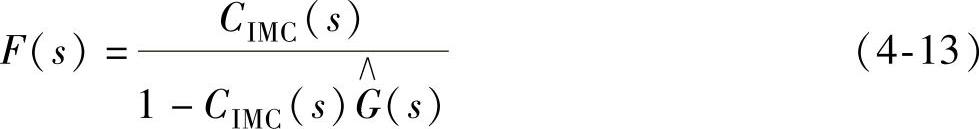
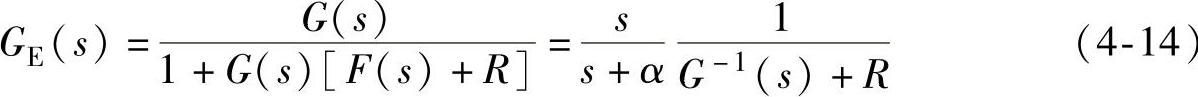
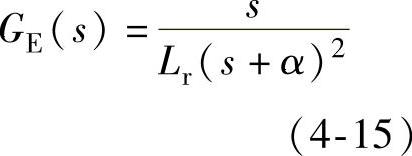
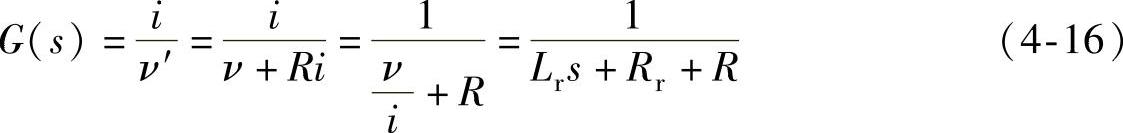
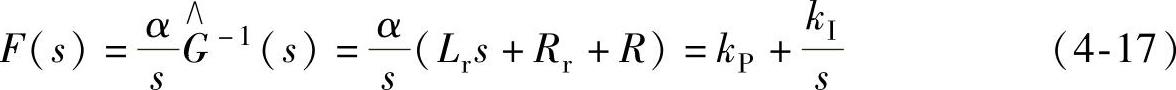






相关推荐