以下内容为满足双馈发电机在绕组匝数不变约束条件下的坐标变换及变换矩阵。绕组匝数不变约束条件下的坐标变换所推导出的系统最贴切地反映了电机的物理特征,由此产生的等效电路中的电感与电机设计者正常计算的电感值相一致,正是这些优点使得这种系统被电力工业和发电机制造厂家广泛使用。......
2023-06-23
在变换前后功率不变,且电压和电流选取相同变换阵的条件下,变换阵的逆与其转置相同,在两相系统上再人为地增加一相零轴磁动势,则构成的这种变换属于正交变换。
设变换前电压矩阵方程为u=ZI
用u′、I′、Z′表示变换后的电压、电流和阻抗矩阵,令

式中,Cu、Ci分别为电压和电流的变换矩阵。
设变换前后两个坐标系统中的功率不变,即

式中,IT,I′T分别为I和I′的共轭转置矩阵。
把式(2-30)中的u、I代入式(2-31),可得到以下关系:
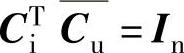
式中,In为单位矩阵。
为简化变换系统,通常取Ci=Cu=C,所以

而
满足式(2-32)的变换矩阵叫单元变换矩阵,这种变换称为正交变换。
又磁链ψ=Cψ′,因为ψ=LI,ψ′=L′I′,所以

式(2-32)是在“功率不变”和电压、电流选取相同的变换阵的条件下得到的。即在这种正交变换中,变换阵C的可逆阵C-1等于变换阵C的共轭转置。如果变换阵C是实数矩阵,即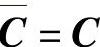 ,那么
,那么
C-1=CT (2-35)
这种变换的优点是变换前后满足功率不变约束和磁动势不变约束条件,其变换阵的逆等于其转置矩阵,此外,采用这种变换时所有互感是可逆的。这种变换存在的问题是变换前后绕组匝数不等,失去了静止坐标系(A、B、C坐标系)和同步旋转坐标系(d、q、0坐标系)下变量之间单位对单位的对应关系。

图2-4 三相/两相变换
2.2.1.1 三相静止到两相旋转(3s/2r)的坐标变换
取垂直的坐标d、q,如图2-4a所示,d轴与定子A相轴线之间的夹角为θ1,d轴与转子a相之间的夹角为θ2,转子a轴超前定子A轴的角度为θ,采用d、q两相系统取代换A、B、C三相系统,这种变换可以看成一种将定子量折算到转子侧的手段,类似于在变压器中用匝数比将二次侧量折算到一次侧。设三相系统每相绕组匝数为N3,两相系统每相绕组匝数为N2,令三相系统总磁动势等于两相系统总磁动势,则有
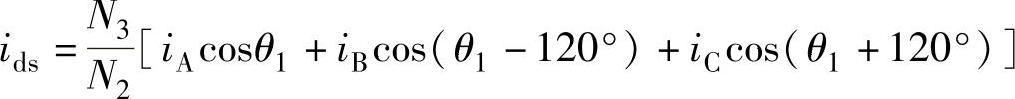

式中,ids、iqs为系统中的定子电流在d、q轴向的分量。
再定义一个零轴电流,设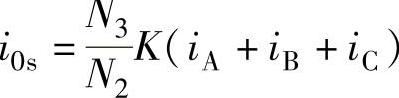 ,则
,则
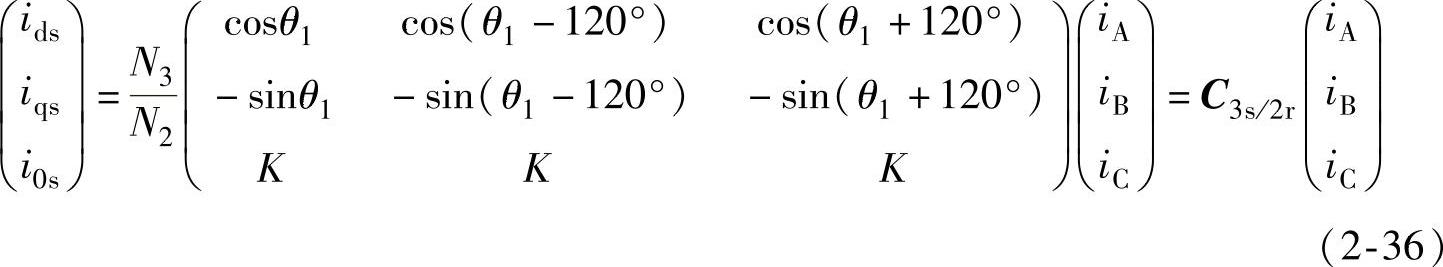
式中,C3s/2r为定子三相A、B、C变换到d、q两相的变换矩阵,即

只要选取K≠0,则行列式|C3s/2r|≠0。对式(2-37)的C3s/2r求逆,可得到
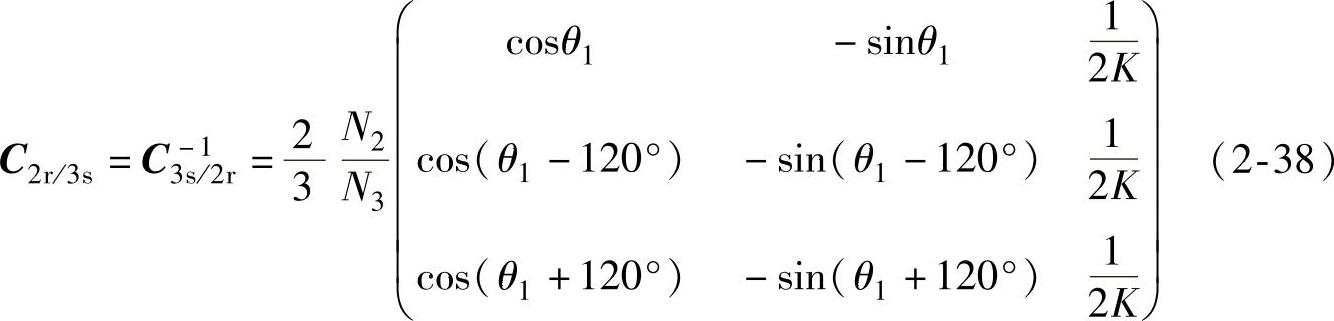
由式(2-36)得到
由于C3s/2r是单元变换矩阵,根据式(2-35)有
由式(2-37)求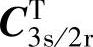 为
为
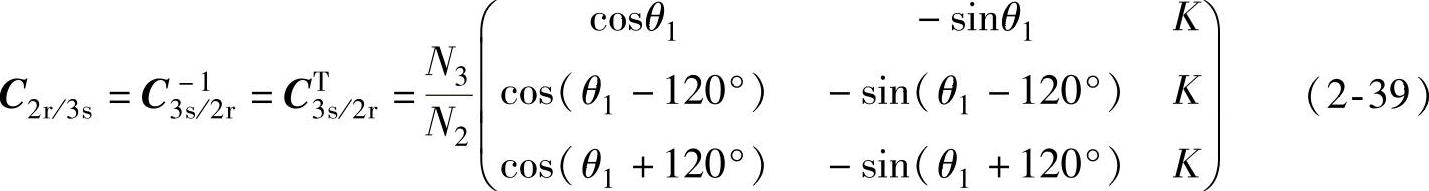
比较式(2-38)和式(2-39),可得到以下关系式:
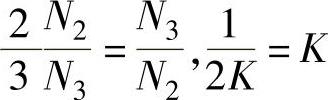
所以
把这两个值代入式(2-38)和式(2-37)可得到
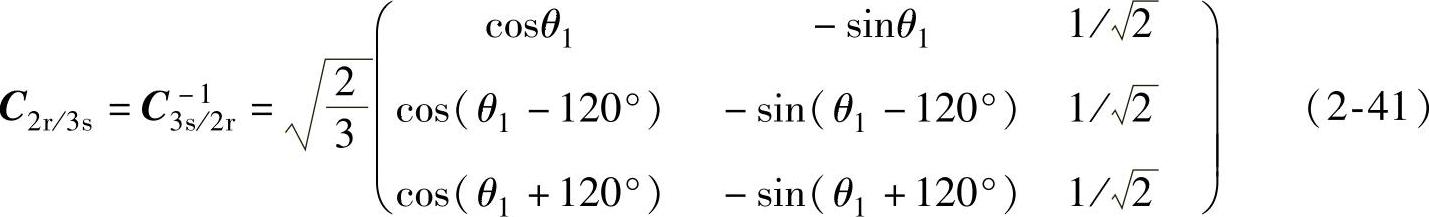

所以有
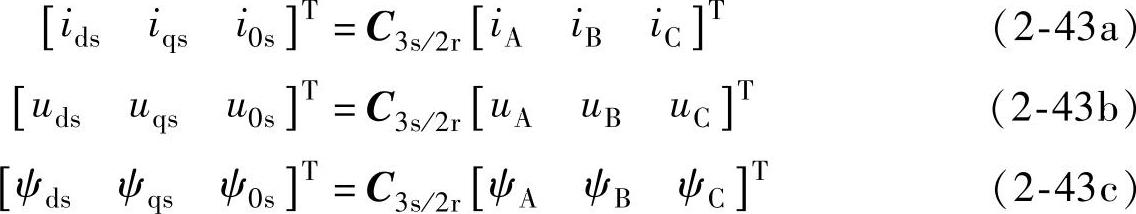
反变换式为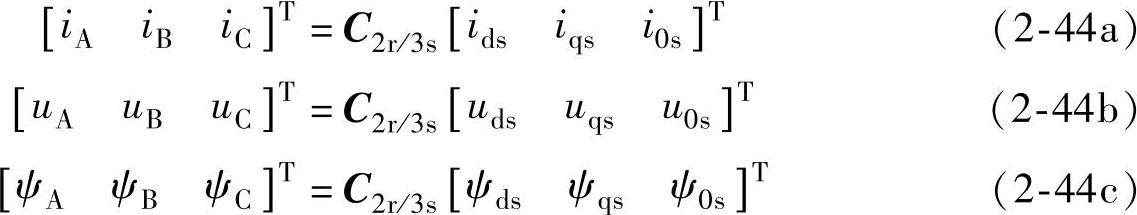
转子电压、电流、磁通从三相变换到d、q两相的变换阵为C3s/2r,将式(2-42)中θ1用θ2代换即可(见图2-4a):
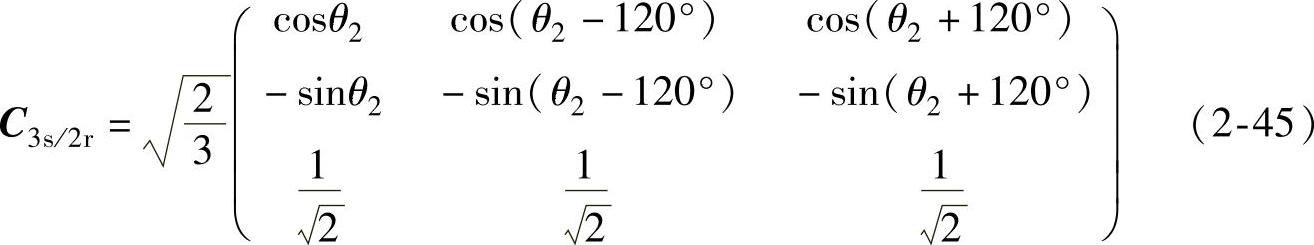
反变换阵为
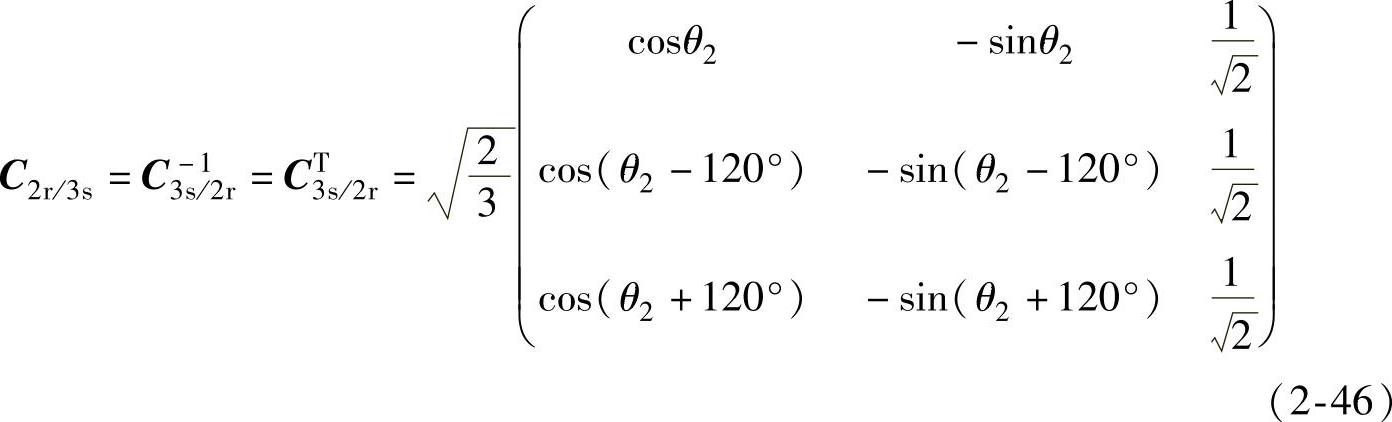
变换式为
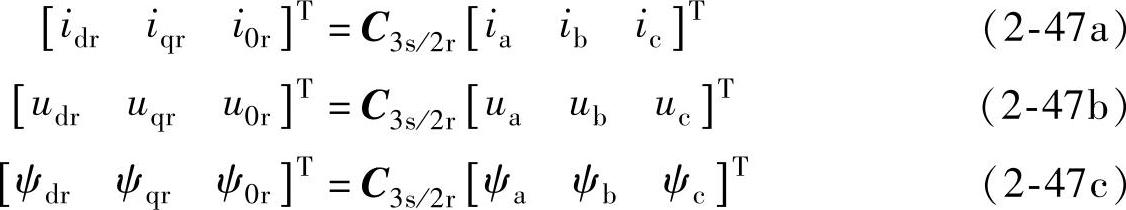
反变换式为
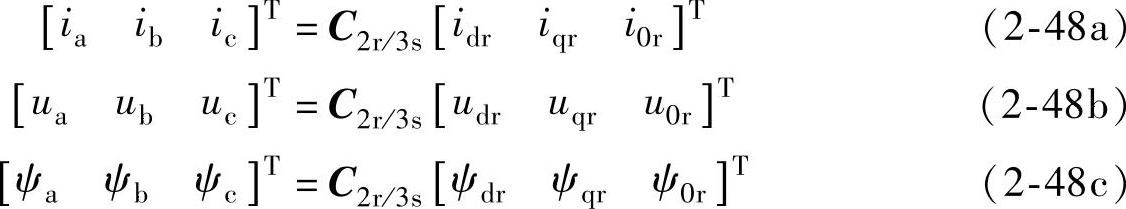
如果d、q轴与定子旋转磁场(也是转子旋转磁场)同步旋转,那么dθ1/dt=pθ1=ω1(ω1是定子旋转磁场角速度),dθ/dt=pθ=ωr(ωr是转子旋转角速度),dθ2/dt=ω2=ωs(ω2是转子转差角速度,ω2=ωs=ω1-ωr)。这种变换被称为同步旋转d、q变换。变换后的系统被称为同步旋转d、q坐标系统。
2.2.1.2 三相静止到两相静止(3s/2s)的坐标变换
如果把两个互相垂直的坐标轴d、q固定在定子上,并且取d的方向与定子A相绕组轴线一致,那么这种变换被称为静止三相/两相变换,为了将它区别于旋转的d、q变换,通常用互相垂直的α、β轴代替d、q轴,并称为α、β变换(α轴类似d轴且与定子A轴同方向),如图2-4b所示。在α、β变换中,因为图2-4a中的θ1≡0,pθ1=0,所以类似于公式(2-42),我们有变换阵
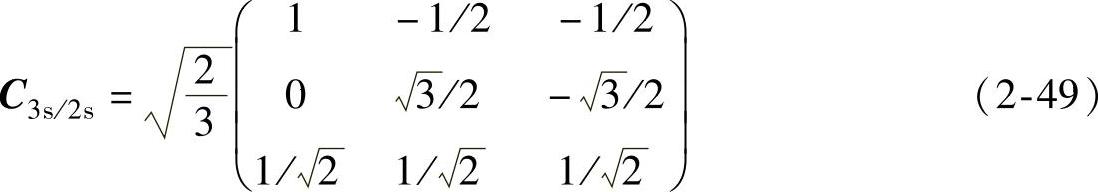
反变换阵为
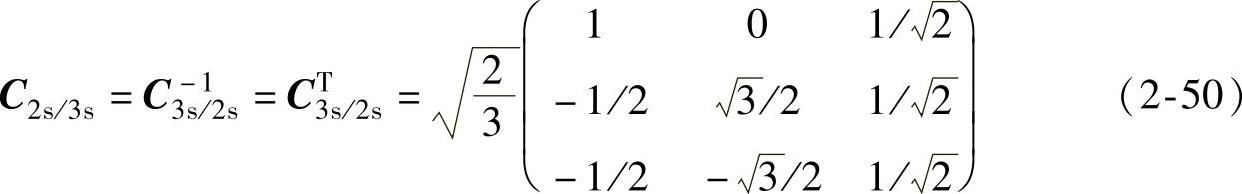
变换式为
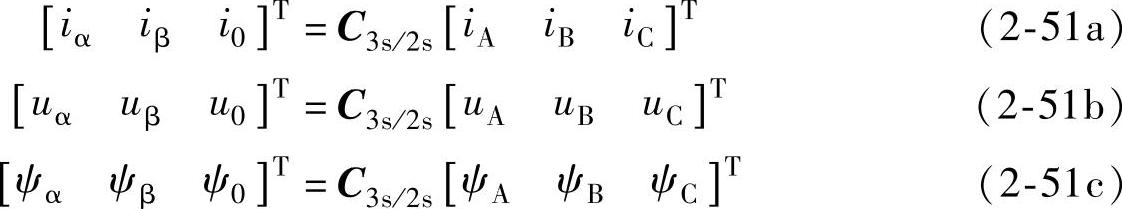
反变换式为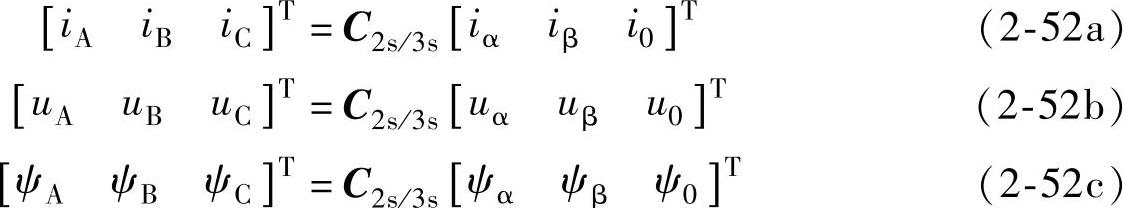
由式(2-49)可知:三相/二相静止变换阵中的元素都是常数(与θ角无关),而在三相/二相旋转变换中,由于两个坐标系统之间有相对运动,变换阵中的一些元素是两个系统之间相位差角θ1(或θ2)的函数,如式(2-42)和式(2-45)所示。
在α、β变换中,若转子各量也变换到与定子相同的α、β系统,则转子变换阵中的某些元素就应该是θ角的函数,而不全是常数。因为原转子a、b、c系统与变换后的α、β系统之间有相对运动,如果我们把转子a、b、c系统中的各量变换到与转子a相绕组相对静止的α、β系统(常取α轴与转子a轴方向相同),那时变换阵中的元素类似于式(2-49),全是常数,这当然也是由于变换前后的两个坐标系统之间没有相对运动之故。
2.2.1.3 两相静止到两相旋转(2s/2r)的坐标变换
由两相静止坐标系α-β到两相旋转坐标系d-q的变换简称2s/2r变换,α轴与d轴的夹角θ1随着时间而变化,令静止的二相系统α、β与旋转的二相系统d、q绕组匝数相同,磁动势相等,则由图2-5可得(以电流为例):
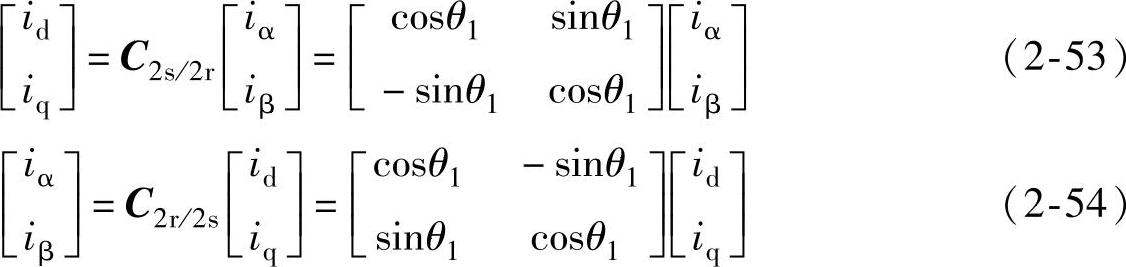
其中,变换矩阵C2s/2r及其反变换矩阵C2r/2s为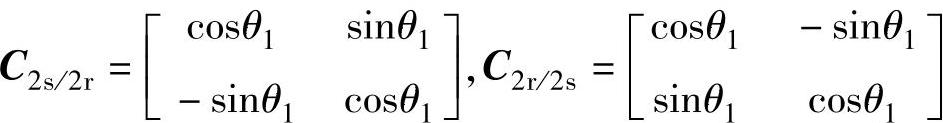 ,可见C2s/2s/2r-1=C2s/2sT=C2r/2s。
,可见C2s/2s/2r-1=C2s/2sT=C2r/2s。
基于功率不变约束条件下的坐标变换在电能质量控制和瞬时无功功率理论方面广为应用,但是正交变换并不与任何特定的有意义的物理情况相一致,当采用变换阵的系数为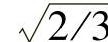 时,等效的d、q轴绕组的匝数是abc绕组的
时,等效的d、q轴绕组的匝数是abc绕组的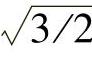 倍,这就失去了静止坐标系和同步旋转坐标系下变量之间单位对单位的对应关系。
倍,这就失去了静止坐标系和同步旋转坐标系下变量之间单位对单位的对应关系。
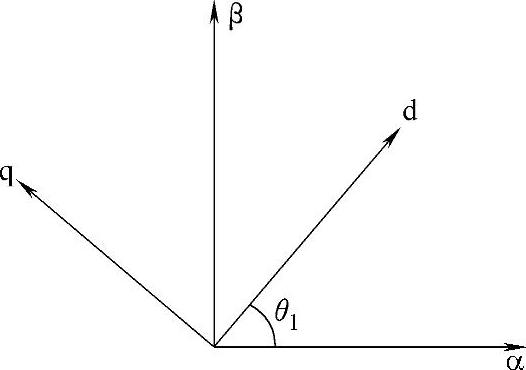
图2-5 二相静止/二相旋转变换
下面对另一种最贴切的反映电机的物理特征的坐标变换——绕组匝数不变约束条件下的坐标变换进行介绍,具体推导和上节类似,只给出相应的结论。
有关双馈式风力发电机组柔性并网运行与控制的文章

以下内容为满足双馈发电机在绕组匝数不变约束条件下的坐标变换及变换矩阵。绕组匝数不变约束条件下的坐标变换所推导出的系统最贴切地反映了电机的物理特征,由此产生的等效电路中的电感与电机设计者正常计算的电感值相一致,正是这些优点使得这种系统被电力工业和发电机制造厂家广泛使用。......
2023-06-23

【主要内容】1.矩阵的初等变换矩阵的下列三种变换称为矩阵的初等行(列)变换:(1)互换矩阵的两行(两列).(2)用一个非零常数c乘矩阵的某行(某列),即用c乘某行(某列)的每个元素.(3)矩阵某行(某列)的k倍加到另一行(另一列),即某行(某列)的每个元素的k倍,加到另一行(另一列)的对应元素.矩阵的初等行变换与初等列变换,总称矩阵的初等变换.2.初等矩阵单位矩阵经过一次初等变换所得到的矩阵,称为......
2023-10-27

坐标变换的思路是,将交流电动机的物理模型等效地变换成类似直流电动机的模式,这样分析和控制就可以大大简化。利用坐标变换就可以求出iA、iB、iC与iα、iβ和im、it之间准确的等效关系。图2-4 旋转的直流绕组按照所采用的条件,电流变换矩阵也就是电压变换矩阵,也是磁链的变换矩阵。由图可见iα、iβ和im、it之间存在关系如式,C2r/2s是两相旋转坐标系变换到两相静止坐标系的变换阵。......
2023-06-19

UIsinφsin2ωt部分是一个2倍系统频率的纯振荡分量,其峰值为UIsinφ。由上述瞬时功率表达式可知,对于单相正弦交流电力系统而言,其瞬时功率并不是恒定的,主要是在直流分量UIcosφ的基础上叠加了一个2倍系统频率的功率振荡分量。传统有功功率的定义为瞬时功率在一个正弦周期内的平均值。该物理量可被理解为用来表示在单位功率因数下可达到的最大有功功率。图2-1 功率三角形图2-1 功率三角形......
2023-06-23

下面将对这两套非正弦条件下的功率分析方法进行简单的介绍。非正弦条件下电能质量的损失还可以通过畸变功率D来描述。畸变功率可按下式定义:D2=S2-P2-Q2 Budeanu的功率定义被广泛应用于非正弦条件下的电路系统分析。但是,只有式定义的有功功率,在正弦和非正弦条件下都具有明确的物理意义。上述方程只是将非正弦条件下的电路作为不同频率激励源的几个独立电路之和来处理。......
2023-06-23

,Ps,使得对所得矩阵再进行列的初等变换,变为即存在一些初等方阵Q1,Q2,…P2P1E=A-1.由于在矩阵的左边乘上一个初等方阵P,相当于对这个矩阵作一个与P相对应的初等行变换.上面两个等式表明,对A依次作P1,P2,…......
2023-11-22

鉴于上述问题,达成包装集团下属的“合肥丹盛包装有限公司”在普通瓦楞纸箱全自动粘箱机上加装矩阵码智能喷印系统,成功解决了矩阵码喷印质量差和效率低下等一系列问题。图7-4-1系统框架图2.各组成部分的工作原理本技术是在普通瓦楞纸箱全自动粘箱机上,加装一套矩阵码智能喷印系统。......
2023-06-27

特征变换是通过一种映射变换改造原特征空间,也就是说新的每一个特征是原有特征的一个函数。二维模式主成分分析[101]或判别分析[102]是近年提出的一种针对图像模式的特征变换方法。特征选择和特征变换都是为了达到维数削减的目的,在降低分类器复杂度的同时可以提高分类的泛化性能。......
2023-06-28
相关推荐