值得注意的是，当稳定安全系数降低至临界值1.0时，即路堤发生失稳破坏时，地基变形系数曲线相应位置处大致出现拐点。当存在软弱层时，地面横坡对变形影响显著，这无疑从理论上证实了《铁路工程地基处理技术规程》根据软弱地基横向坡度大小修正稳定安全系数是合理的。图5-5不同路堤高度下地基变形系数与路堤稳定安全系数关系......
2023-10-03
研究系统参数的影响规律
【摘要】：表8.8不同节气门开度下的发动机合力矩图8.30进气压降与转速和节气门开度的关系结合已建立的发动机阻力矩模型，可以求得不同节气门开度对应的最大阻力矩、最小阻力矩和平均阻力矩。这个过程中，转矩关系必须满足该关系式表示了电流的暂态变化过程，电流大小的影响因素包括定子绕组的电感、电阻和PWM占空比。
发动机在进气过程中，外界新鲜空气主要受到局部阻力和沿程阻力的影响，由于空气的黏度很小，沿程阻力损失可忽略不计。发动机进气过程的局部阻力损失主要来自节气门和进气歧管。该过程发动机的进气压降可以表示为
式中，Δp为进气压降；ξm为局部阻力系数；wn为气体流动速度；ρh为气体的密度。
由于转子发动机进气口连接化油器直通外界空气，所以管道中的局部阻力系数即节气门处的局部阻力系数。当节气门开度不同时，其阻力系数也不相同，具体关系如表8.7所示。
表8.7 节气门开度与局部阻力系数的关系
计算中应注意进气速度和发动机转速的区别，由于转子发动机为旋转机构，因此将转速（r/min）转换为线速度（m/s），取平均值作为公式中的气体流动速度进行计算。将局部阻力系数以及发动机各个转速代入式（8.60），可以得到不同节气门开度和不同发动机转速情况下的进气压降，如图8.30所示。
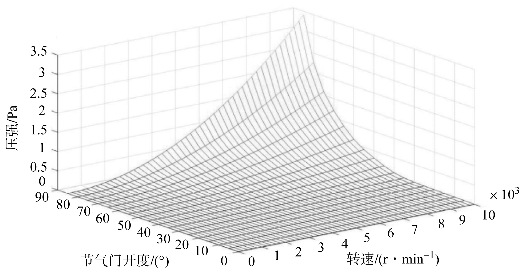
图8.30 进气压降与转速和节气门开度的关系
结合已建立的发动机阻力矩模型，可以求得不同节气门开度对应的最大阻力矩、最小阻力矩和平均阻力矩。由于离心力的变化规律与转速有关，与压降无关，因此压降对阻力矩产生的影响可以仅通过气体阻力矩和摩擦阻力矩相加的合力矩（以下简称为合力矩）来验证。将运算结果记录如表8.8所示。
表8.8 不同节气门开度下的发动机合力矩
表8.8中的数据处理后得到最大合力矩和最小合力矩的变化率曲线，如图8.31所示。
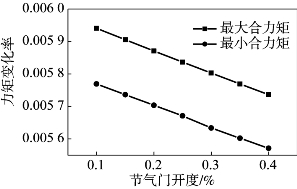
图8.31 力矩变化率曲线
从图8.31可以看出，节气门开度对发动机因进气压降导致的力矩值的变化很小，基本上可以忽略不计。由于转子发动机一个循环同时有三个燃烧室参与工作，旋转过程中，进气压降对某一燃烧室力矩的影响因叠加作用会被很大程度地抵消，故整体上节气门开度对阻力矩基本没有影响。
发动机正常启动过程，仍需要加浓过后的燃油混合气体，因此，节气门开度不宜过大，一般不超过10%。
2.电动机结构参数对启动性能的影响
1）启动初始阶段
在启动初始阶段，定子绕组内的电阻和电感带来的阻抗影响，使得电流无法迅速增加，具有一定的延迟性。而电流大小直接影响着电动机的输出力矩，电动机输出力矩小于发动机提供的负载转矩，电动机仍处于静止阶段。电流的延迟效应与发动机提供的负载转矩、定子绕组的电感电阻、PWM调制方法有很大关联，这些因素均对启动初始阶段的持续时间有决定性作用。
当系统处于启动的初始阶段时，电动机的定子绕组可由图8.32表示。
图8.32将定子绕组简化为电压源外加电感和电阻，其关系式为
图8.32 电动机定子结构简图
式中，Us为电动机端电压；D为PWM占空比；is为电动机定子电流；Rs为电动机相电阻，Ls为定子等效电感。
对上式进行数学变换，可得电流的变化关系
该关系式表示了电流的暂态变化过程，电流大小的影响因素包括定子绕组的电感、电阻和PWM占空比。
定子电流不断变大，直到对应的电动机的输出转矩大于发动机提供的负载转矩，电动机开始带动发动机运转。这个过程中，转矩关系必须满足
发动机提供的负载转矩一般是不变的，由前面阻力矩计算仿真部分可知，发动机的静摩擦阻力矩为0.07 N·m。转矩与电流的关系式为
联立上式，可得系统启动瞬时的电流is
进而求出启动初始阶段所需的时间t
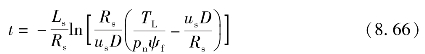
由式（8.66）可以看出，启动初始阶段的持续时间受到电动机基本参数、定子绕组电感Ls、相电阻Rs和占空比D等因素的影响，根据推导的关系式，搭建计算模型，可以得到上述几个因素对该阶段时间t的影响规律，如图8.33～图8.35所示。
图8.33 不同占空比条件下的电流曲线
由图8.35可知，定子绕组电感Ls对该阶段时间t的影响最明显，这主要是因为电感的存在会使电流存在一定的延迟效果，Ls越小，延迟影响越小，t 越小。电感的存在抑制电流迅速增加，可以保护三极管不致被瞬时大电流击穿，有利于延长逆变器的寿命。PWM占空比D对时间t的影响较大，占空比越大，通过电源电压逆变得到的电动机供电电压就越大，从而使电动机电流增大，转速上升。电阻的影响主要是通过电流来实现的。电动机可等效为理想电压源、内阻、电感的电路形式，当电阻越大时，电流越小，电动机转速上升越慢，电动机启动时间变长。
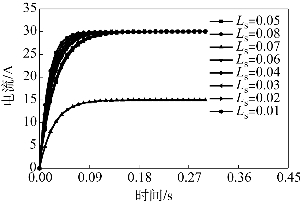
图8.34 不同电感条件下的电流曲线
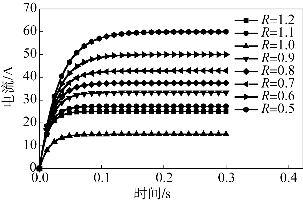
图8.35 不同电阻条件下的电流曲线
2）启动加速阶段
发动机启动过程的总时间分为初始阶段时间和加速阶段时间，为缩短总时间，同样需要研究如何缩短加速阶段的时间。接下来分析电感Ls和电阻Rs对发动机启动时间的影响。电动机采用最大转矩/电流的控制策略，假设发动机阻力矩恒定，则启动加速阶段电机的基本方程如下。
电流转换方程：
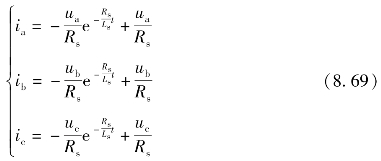
转矩方程：
运动方程：
图8.36所示为不同电感系数情况下，启动过程中发动机转速随时间的变化曲线，电感系数分别为0.0002H、0.0005H、0.0008 H。从图8.36可以看出，不同电感值条件下启动转速曲线几乎重合，所以近似认为电感系数对发动机的启动加速时间没有影响。
图8.36 不同电感系数对转速的影响
图8.37所示为不同电阻值情况下，转速随时间的变化关系。从图8.37可以看出，当电阻值小于0.5Ω时，转速曲线近乎重合，电阻Rs对发动机转速变化基本上没有影响。这主要是因为在电动机闭环控制中具有限流环节。当电阻降低，电流增大，直到达到限幅值。当电阻值大于0.5Ω时，发动机启动加速时间随电阻值发生较大变化，电阻取值不合适时，将使启动时间过长。为保证系统具有快速的启动性能，电动机的电阻值应控制在0.5Ω以下。
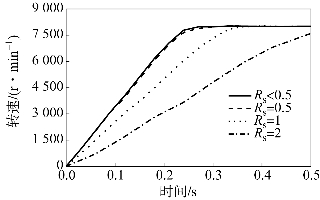
图8.37 不同电阻值对转速的影响
3.转动惯量对启动性能的影响
启动阶段，电动机拖动发动机运转。根据数学关系，在驱动力矩和负载转矩不变的情况下，发动机角加速度与旋转部件的转动惯量成反比。系统转动惯量的大小与启动时间密切相关，进而会影响系统的能量损耗。因此有必要探究转动惯量对启动性能的影响。假定电动机的驱动转矩为0.15 N·m，发动机平均阻力矩大小为0.1 N·m，则转动惯量对角速度的影响如图8.38所示。
图8.38 不同转动惯量下角速度曲线
从图8.38可以看出，转动惯量越大，系统启动时间越长，两者呈线性关系。若以发动机启动转速为8 000r/min，经单位换算后，对应角速度为837 rad/s，可以得到不同转动惯量对应的启动时间。
参考汽车行业对混合动力汽车启动时间的规定，以0.4 s作为发动机启动标准，则系统整体的转动惯量不应超过2.45 kg·m2。为提高启动性能，缩短启动时间，应尽量减小负载的转动惯量。
4.电动机能量消耗分析
启动过程中，电动机作为启动电机，对外做正功，消耗能量。在二维旋转坐标系中，可通过下式表示启动过程的能量消耗We。
启动过程中，电动机采用最大转矩/电流的控制策略，因此id=0。上式可以表示成
而电动机q轴电压和电流存在如下关系：
因此，电动机消耗的功可以表示为
图8.39所示为电动机相电阻Rs分别取不同值时，电动机消耗功随时间变化的关系。从图8.39可以看出，不同大小的电阻值对电动机消耗功的影响程度不同。当电阻小于0.1Ω时，电阻值的影响很小，故曲线几近重合。电阻值大于0.1Ω 小于1Ω时，电动机消耗功曲线增长较为缓慢，不同阻值之间差异较小。当电阻大于1Ω时，电动机消耗功随时间变化幅度明显加快，且不同阻值之间差异显著。
图8.40所示为不同电感系数下，电动机做功随时间的变化关系。图8.39中共有六条曲线，电感值分别为0.0002H、0.0005H、0.0008H、0.001H、0.001 5H、0.002 H。从图8.40中可以看出，不同电感值对应的曲线重合交错，电感值的不同对电动机启动过程做功基本没有影响。
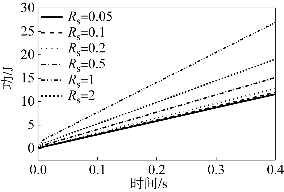
图8.39 不同电阻值下电动机做功随时间的关系
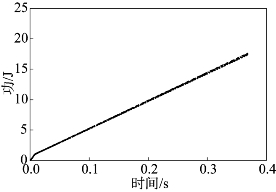
图8.40 不同电感系数下电动机做功随时间的关系
因此，从减小电动机启动过程能量消耗的角度考虑，电感可选为当前值0.00016H，电阻应小于0.5Ω。
另外，电动机的转速也受电感系数的影响。为使电动机具有足够的动力性，电动机所达到的最小极限转速应大于发动机的启动转速。其关系式为
式中，nb为电动机最低转速；ulim为电动机的极限电压；pn为电动机极对数；Lq为q轴等效电感；ilim为电动机极限电流；ψf为永磁体在定子上耦合的磁链。
当发动机启动设定转速为8 000r/min时，电动机最低转速应大于启动设定转速，经计算电感必须小于0.0003 H。
总结上文的分析过程，电动机电感应小于0.0003H，电阻应小于1Ω，系统整体的转动惯量应小于2.45 kg·m2，以保证电动机启动发动机时启动性能较好，功率消耗最低。
有关小型转子发动机数值建模与仿真分析的文章
- 详细阅读
- 详细阅读
-
矛盾规律研究：系统规律与适用范围不同详细阅读
第一节系统规律与矛盾规律的适用范围不同近年来，学术界一些同志提出，系统规律关于事物是具有复杂层次的动态系统比事物是矛盾的两个对立方面组成的思想，能更好地反映、说明事物的内在复杂结构，系统规律不但是一条普遍的规律，而且它已经把矛盾规律的一切合理因素作为一个环节包含在其中了，因而系统规律是对矛盾规律的发展与深化。因此，系统规律不是如同矛盾规律一样的普遍规律，它只能是适用于事物一定状态的特殊规律。......
2023-11-28
-
研究结果：系统规律与矛盾规律性质不同详细阅读
系统规律中心之点是强调总体协调。系统规律就是适用于局部组织化区域的规律，也就是适用于稳态或个体同一性的规律。维纳没有忘记系统的有序、组织化只是一个暂时的阶段，这不无意义。从马克思主义观点来看，即使是信息占统治地位的时候，美国也仍然是一个垄断的资本主义社会，它的基本性质不会改变。......
2023-11-28
-
视觉测量技术：系统结构参数对测量精度的影响分详细阅读
式有时还写为以为观测值的正直摄影精度估算当以为观测值时，式可写为不考虑摄影基线误差mB和主距误差mf，而以为误差源，式的微分式为或写为转为中误差形式，并认定mx1=mx2=my1=m，则有式和式是近景摄影测量中，以正直摄影方式进行摄影时，对精度预先实施粗略估算的常用式。7）两台摄像机的有效焦距越大，视觉测量系统的测量精度越高，即采用长焦距镜头容易获得较高的测量精度。......
2023-11-24
-
高速离心纺丝工艺参数对射流影响优化研究详细阅读
以6%的PEO溶液为实验材料，在纺丝速度为2500 r/min、3500 r/min、5500 r/min、7500 r/min下进行高速离心纺丝射流实验，制备的PEO纳米纤维扫描电镜图如图7-16所示。断裂的纤维缺乏张力，蓬松无力，过高的纺丝速度和射流速度反而会使得纤维的性能降低。研究高速离心纺丝过程中电动机的转速与纺丝溶液射流运动的关系对制备良好的纳米纤维有着重要的意义，对于不同的纺丝溶液，选择合适的电动机转速是制备质量优秀的纳米纤维的关键因素。......
2023-06-23
-
气割号料及工艺参数的影响详细阅读
工件下面的空间不能密封，否则会在气割时引起爆炸。工艺参数对气割的质量影响很大。开始切割时，若预热钢板的边缘至略呈红色时，将火焰局部移出边缘线以外，同时慢慢打开切割氧气阀门。当到达终点时，应迅速关闭切割氧气阀门，并将割炬抬起，再关闭乙炔阀门，最后关闭预热氧阀门。图5-12 手工气割a）预热 b）上提 c）吹渣 d）切割3.气割允许偏差气割的允许偏差应符合表5-12规定。......
2023-08-22
-
焊接参数对焊缝成形的影响详细阅读
埋弧焊焊接参数的选择对焊缝成形和质量有着重要影响。图7-19 焊丝伸出长度对焊丝熔敷率的影响图7-20 焊丝伸出长度对焊缝熔深的影响6.电源种类与极性电源种类和极性可以改变焊缝的形状和尺寸。焊剂与焊丝合理匹配是获得高质量焊缝的关键，......
2023-07-02
相关推荐