首页理论教育永磁电动机仿真模型优化技巧

永磁电动机仿真模型优化技巧

2023-06-23 理论教育版权反馈

【摘要】：图8.18所示为三相永磁电机的部分模块仿真模型。图8.16旋转坐标系下的PMSM等效模型2.永磁电动机的仿真模型根据永磁电动机的数

1.永磁电动机的数学模型

为使分析过程更为简单，假设电动机为理想电动机，且满足以下条件：

（1）不计电动机铁芯的饱和；

（2）忽略电动机的涡流和磁损；

（3）供电电流为理想的三相正弦波电流。

1）自然坐标系

自然坐标系下的电动机三相电压方程为[2，3]

磁链方程为

式中，Ψ3s为三相绕组的磁链；u3s、R、i3s分别为三相绕组的相电压、电阻和电流；L3s为三相绕组的电感；F3s（θe）为三相绕组的磁链，且满足

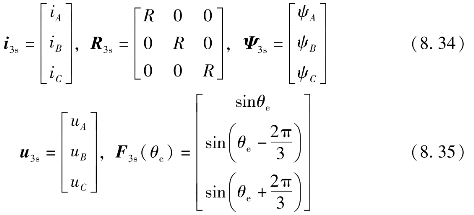
pagenumber_ebook=252,pagenumber_book=242

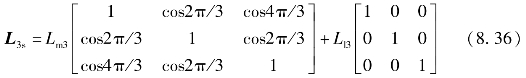
pagenumber_ebook=253,pagenumber_book=243

式中，Lm3为定子互感；Ll3为定子漏感。

由机电能量互换关系可知，电磁转矩Te等于磁场储能对机械角θm位移的偏导，因此有

式中，pn为电动机的极对数。

另外，电动机的机械运动方程为

式中，ωm为电动机的机械角速度；J为转动惯量；B为阻尼系数；TL为负载转矩。

以上各式即为永磁同步电动机在三相坐标系下的基本数学模型。从以上关系式易知，电动机的数学模型是一个复杂且强耦合的多变量系统，为便于控制，必须选择合适坐标系进行降阶和解耦变换。

2）两相（α-β）静止坐标系

为简化自然坐标系下三相永磁同步电动机的数学模型，采用的坐标变换通常包括静止坐标变换（Clark变换）和同步旋转坐标变换（Park变换）。即将电动机的数学模型从三相静止坐标系转换到两相静止坐标系下，然后从两相静止坐标系转换到两相旋转坐标系。

从三相静止坐标系变换到两相静止坐标系的过程是将三个坐标轴的空间矢量通过Clark变换矩阵转换成两相空间矢量坐标系下的两个投影分量。根据坐标系之间的关系，可以得到坐标变换公式：

式中，f代表电动机的电压、电流或磁链等变量；T3s/2s为坐标变换矩阵，可表示为

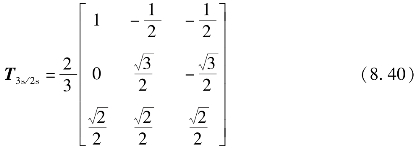
pagenumber_ebook=253,pagenumber_book=243

将静止坐标系α-β变换到自然坐标系ABC的坐标变换称为反Clark 变换，可以表示为

式中，T2s/3s为坐标变换矩阵，可以表示为

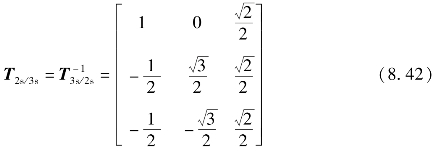
pagenumber_ebook=254,pagenumber_book=244

以上简单分析了自然坐标系的变量与静止坐标系的变量之间的关系，变换矩阵前的系数为2/3，是根据幅值不变作为约束条件得到的。此外，对三相对称系统而言，在计算静止坐标系下的变量时，零序分量f0可忽略不计。

3）两相（d-q）旋转坐标系

从三相静止坐标系到两相静止坐标系变换后，再进行将矢量从两相静止坐标系变换为两相旋转坐标系的过程，称为Park变换。坐标变换公式如下：

式中，T2s/2r为坐标变换矩阵。记静止坐标系α轴与旋转坐标系的d轴夹角为θ，T2s/2r可以表示为

pagenumber_ebook=254,pagenumber_book=244

将同步旋转坐标系d-q变换到静止坐标系α-β的坐标变换称为反Park变换，可表示为

式中，T2r/2s为坐标变换矩阵，可表示为

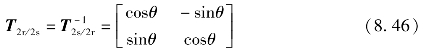
pagenumber_ebook=254,pagenumber_book=244

进而可以得到旋转坐标系下的数学模型。

电压方程[4]：

pagenumber_ebook=254,pagenumber_book=244

式中，ωr为转子角频率；id、iq分别为d-q绕组等效电流；ud、uq分别为d-q绕组等效电压；Ld、Lq分别为d-q绕组等效电感。

d-q坐标系下磁链方程为

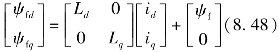
pagenumber_ebook=255,pagenumber_book=245

式中，id、iq分别为d-q轴电枢电流；Ld、Lq分别为d-q轴的电感；ψf为永磁体产生的磁链。

电磁转矩方程为

式中，pn为极对数。

旋转坐标系下的PMSM等效模型如图8.16所示。

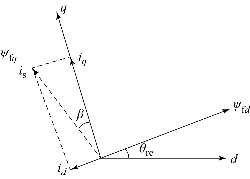
pagenumber_ebook=255,pagenumber_book=245

图8.16　旋转坐标系下的PMSM等效模型

2.永磁电动机的仿真模型

根据永磁电动机的数学模型，在MATLAB/Simulink环境下搭建了三相永磁同步电动机本体的仿真模型，如图8.17所示。该模型是基于二维旋转坐标系搭建的电动机仿真模型。

图8.18所示为三相永磁电机的部分模块仿真模型。