列入危险品管理的包装气体主要包括压缩气体、液化气体、冷冻液化气体和溶解气体四种。在压缩气体或液化气体中，约有54.1%是可燃气体，有61%的气体具有火灾危险。压缩气体和液化气体的标志如图3-2所示。此类气体毒性大，吸入后可引起人体中毒甚至死亡，有些还能燃烧。......
2023-10-28
计算压缩气体阻力矩的方法
【摘要】：图8.1工作室容积的变化2.气缸内工作室的气体压力计算将偏心臂与长轴夹角称作偏心轴转角，该角度为0°时，将该位置定为循环起点，此时容积最大的工作室定为第一工作室。图8.2第一、二、三燃烧室压力曲线3.偏心轴的切向力偏心轴的切向力与气体压力的分量密切相关。将气体合力分解为切向力与法向力，切向力与偏心臂垂直，其正方向定为旋转方向。
当发动机处在启动过程时，计算气缸内的压力时做如下假设：①当发动机在进排气状态时，缸内压力即为进气压力；②当发动机在压缩和膨胀状态时，缸压变化满足绝热过程。
计算公式如下：
式中，Pg、Vg分别为发动机压缩及膨胀行程任意时刻的缸压和气缸容积；Pe、Ve分别为发动机进气终止时的缸压和气缸容积；n为发动机平均绝热指数，n=1.4。
1.气缸工作容积
如果气缸宽度为B，则气缸内单工作室理论容积为
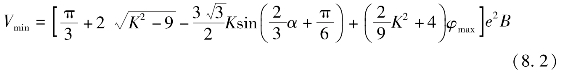
式中，B为气缸宽度；K为形状参数，K=R/e；φmax为最大摆动角；α为偏心轴转角。
当偏心轴转角为π/2 或者3π/2时，转子处于上止点位置，此时工作室的容积最小。因此，该时刻的工作室容积为
当偏心轴转角为0 或者2π时，转子处于下止点位置，此时工作室的容积最大。因此，该时刻的工作室容积为
根据转子发动机的结构设计，偏心轴转角与工作室容积的关系如图8.1所示。
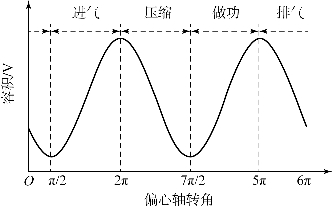
图8.1 工作室容积的变化
2.气缸内工作室的气体压力计算
将偏心臂与长轴夹角称作偏心轴转角，该角度为0°时，将该位置定为循环起点，此时容积最大的工作室定为第一工作室。转子沿规定方向旋转时，其反向按顺序分别为第二工作室和第三工作室。
三个工作室的偏心轴转角分别表示为a1、a2、a3，且把第一工作室作为基准，则有
以pg1、pg2、pg3分别表示相应三个工作室的气压，且分别作用于各自的转子工作面上，其产生的总作用力均过转子中心。因为转子工作面为一曲面，其有效受压面积为转子相邻两顶角连线的长度与转子宽度的乘积。因此，三个工作室的转子有效工作面的瞬时气体力分别为
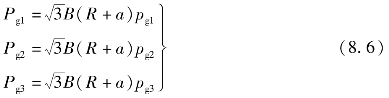
式中，Pg1、Pg2、Pg3分别为第一、二、三工作室作用于相应的转子有效工作面的瞬时气体力；B为气缸宽度；pg1、pg2、pg3分别为第一、二、三工作室的气体压力；R为创成半径；a为平移距。
由于转子发动机有三个燃烧室，每个燃烧室相位不同，因此在模型搭建时需要考虑判定条件，判断该时刻燃烧室内的气体是否处于绝热过程。第一个燃烧室的四个冲程随偏心轴转角的变化关系如图8.1所示，判断该燃烧室处于哪一个冲程的逻辑关系如表8.1所示。
表8.1 四个冲程的逻辑关系判断
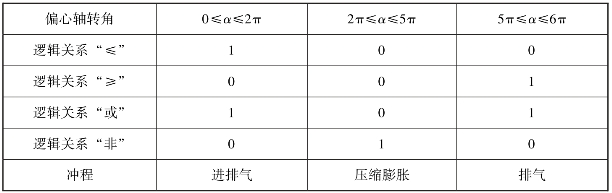
根据前文的公式以及表8.1的逻辑关系，搭建该燃烧室的气体压力的计算模型，由该仿真模型可以计算得到第一燃烧室的压力变化曲线，进而可以得到第二和第三燃烧室的压力变化曲线，如图8.2所示。
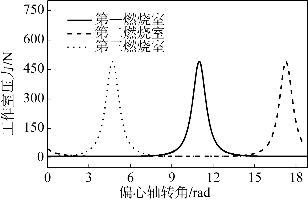
图8.2 第一、二、三燃烧室压力曲线
3.偏心轴的切向力
偏心轴的切向力与气体压力的分量密切相关。如果采用气缸长轴和短轴构成的坐标系计算气体合力，将使得大小、方向随偏心轴不断变化的气体合力难以清晰准确地表示。为此，将坐标系固定在坐标轴上，则气体合力的分析过程将变得清晰。将气体合力分解为切向力与法向力，切向力与偏心臂垂直，其正方向定为旋转方向。法向力与偏心臂同线，其正方向定为指向气缸方向。为了运算方便，切向力与法向力也用单位转子有效工作面积的作用力来表示，称为单位切向力与单位法向力，即
式中，pg为转子瞬时单位气体合力；T为瞬时单位切向力；N为瞬时单位的法向力。
由于转子三个工作面所对应的是同一偏心轴位置，只是相位不同，因此，瞬时的单位切向力为三个工作面瞬时单位切向力的代数和，瞬时单位法向力为三个工作面瞬时单位法向力的代数和，即
式中，T1、T2、T3分别为第一、第二、第三工作面瞬时单位切向力。
故有如下的关系：
经过仿真运算，可得三个燃烧室产生的偏心轴切向力随偏心轴转角的变化曲线，如图8.3所示。
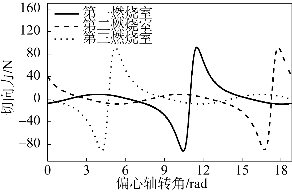
图8.3 第一、二、三燃烧室切向力
4.气体压力产生的偏心轴扭矩
根据前文阐述，单位切向力垂直于偏心臂，且其作用线通过转子中心。由于转子与偏心轴不同心，所以气体压力会对偏心轴产生转矩，其正方向定为转子旋转方向。故单位转子的有效工作面积的扭矩为
式中，T为单位转子的有效工作面积的切向力；e为偏心距。
由式（8.11）可知，偏心距e为常数，所以单位扭矩的变化规律与单位切向力的变化规律完全相同。由于转矩波动较大，一般会在偏心轴上配置转动惯量大的飞轮，可减小转速的不均匀性。
由以上物理量的关系，在Simulink平台上建立发动机气体阻力矩计算仿真模型，并进行仿真计算。气体阻力仿真模型及计算结果如图8.4所示。
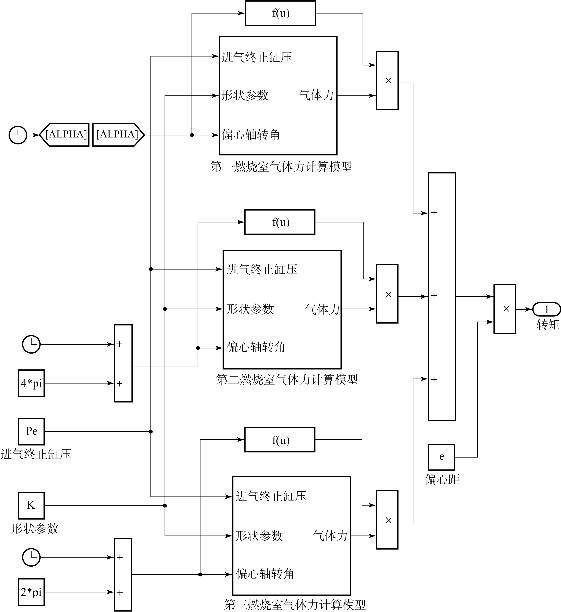
图8.4 气体阻力矩仿真模型及计算结果
由气体引起的偏心轴扭矩仿真结果如图8.5所示，可以看出，转子发动机一个循环（偏心轴转角为0～6π）内，由燃烧室内的缸压产生的阻力矩呈现周期变化。
有关小型转子发动机数值建模与仿真分析的文章
- 详细阅读
-
马赫数与气体压缩性探讨详细阅读
马赫数是指气体的流动速度v与声速c的比值，用符号Ma表示，即马赫数是一个量纲一的参数，常用来衡量气体流动的快慢。马赫数的另一个特征，即反映气体的压缩量。即使压缩性大的气体，如果其流动速度较低或者是静置状态，即气体的马赫数较小，气体的压缩量仍然较小或者为零；反之压缩性小的气体，如果其流动速度较高，即马赫数较大，则气体的压缩量也会比较大。......
2023-08-20
-
压缩气体气瓶的安全使用与搬运技巧详细阅读
（二）气瓶的移动与运输压缩气体和液化气体气瓶在搬动过程中具有很大的危险性，只有采取相应的安全措施，才能保证搬运的安全。1）在搬动存放气瓶时，应装上防震垫圈、旋紧安全帽，以保护开关阀，防止其意外转动和减少碰撞。氢气与空气混合极易引起自燃、自爆，氢气应单独存放，最好放置在室外专用的小屋内，以确保安全，严禁放在实验室内；严禁烟火；应旋紧气瓶开关阀。......
2023-06-23
-
装压缩气体气瓶使用注意事项详细阅读
⑥钢瓶内气体不能用尽，以防其他气体倒灌。⑦钢瓶必须专瓶专用，不得擅自改装，以免性质相抵触的气体相混发生化学反应而发生爆炸。腐蚀性气体钢瓶两年检验一次。⑨气瓶失火，应根据不同气体采取不同的灭火措施，如水流、二氧化碳等。氧气是强烈的助燃气体，纯氧在高温下活泼。因此，盛装乙炔用的器材不能使用含银或含铜量70%以上的合金。充装后的乙炔气瓶要静止24h后使用。钢瓶内乙炔压力降至2.9×105～4.9×105Pa时停止使用。......
2023-10-28
-
如何计算摩擦力矩？详细阅读
转子发动机的摩擦力主要来自密封片与气缸壁之间的径向摩擦力和转子端面与前后端盖的端面摩擦力。图8.10密封片径向惯性力密封片处于型面的长轴和短轴时，FR分别为最大和最小。从图8.11可以看出，由密封片径向合力产生的摩擦阻力矩在一个循环存在三次峰值。图8.11径向合力产生的摩擦阻力矩图8.11径向合力产生的摩擦阻力矩......
2023-06-23
-
如何计算离心阻力矩？详细阅读
其大小为式中，mr为转子组质量；Gr为转子组重量；e为偏心距；ω为偏心轴角速度；n为偏心轴转速；g为重力加速度。转子组质量包括转子体及其内部所含的相位齿轮、偏心轴承等，在转速不变的情况下，转子组离心惯性力的大小为定值，其方向是沿着偏心臂而背向偏心轴中心。为计算方便起见，转子组的离心惯性力也以单位转子有效工作面积的作用力来表示，即......
2023-06-23
-
力矩分配法计算无节点线位移的结构详细阅读
力矩分配法适用于计算无节点线位移的刚架和连续梁。这样的状态称为一个力矩分配单元。 用力矩分配法计算图1.8-6所示结构。图1.8-7 图1.假定当L1=6m，L2=8m，L3=5m，该梁弯矩分配系数μBA及B支座的不平衡弯矩ΔM应与下列（ ）组数据相近。C支座左右两端分配系数为0.4，0.6；固端弯矩为150kN·m、-120kN·m，试问该梁进行二次弯矩重分配，B、C支座的弯矩接近（ ）组数据。......
2023-08-28
-
如何计算附加制动器的制动力矩？详细阅读
从上述附加制动器设计要求分析，基本上就是要解决满足制停距离和减速度的问题，而这两个参数与制动力矩有关，也就是如何确定最佳的制动力矩值以满足整体需要的问题。附加制动器的制动力矩需要满足以下条件：1）制动力矩应大于静态制动力矩以使自动扶梯保持静止状态。2）在上述三种失效模式情况下，制动力矩应大于最小制动力矩，而小于最大制动力矩，以同时满足最大加速度和制动距离的要求。......
2023-06-15
相关推荐