目前，空化流动数值模拟方法基本分为界面追踪法和界面捕获法两类，其中又以界面捕获法中的均相流模型应用最广。在空化流动数值计算中，湍流模型的选择对数值模拟结果的影响很大，尤其是在雷诺数比较高的工程问题中。近年来，在空化流动数值模拟方面，国内学者也取得了有效成果。钟诚文和汤继斌［57］通过引入混合密度函数发展的空化模型，对绕水翼的空化流动进行数值模拟，验证了此方法的可靠性。......
2025-09-29
湍流模型及其应用于流体数值模拟的研究
【摘要】：湍流的重要特点是物理量的脉动，目前描述湍流流动的数值模拟方法主要包括直接数值模拟、大涡模拟和分离涡模拟等。分离涡模拟方法是将大涡模拟和雷诺平均方法结合，在壁面处采用分离涡模拟方法，在湍流的核心区域采用大涡模拟方法。模型考虑了网格的各向异性，且调整亚网格长度尺度来实现RANS向LES的过渡。除此之外，为解决近壁雷诺应力估计不足的问题，IDDES模型中增加新项fe。
内燃机整个工作循环中，其缸内气体充量始终进行复杂而又强烈瞬变的湍流运动。湍流的重要特点是物理量的脉动，目前描述湍流流动的数值模拟方法主要包括直接数值模拟、大涡模拟和分离涡模拟等。直接数值模拟和大涡模拟的计算时间成本过高，造成资源的浪费。分离涡模拟方法是将大涡模拟和雷诺平均方法结合，在壁面处采用分离涡模拟方法（DES），在湍流的核心区域采用大涡模拟方法（LES）。在大涡模拟计算中，壁面处采用LES方法几乎会占用一半的计算时间。考虑到计算量的问题，分离涡模拟方法是非常合适的选择。分离涡方法将随机变化的湍流瞬时量分解为统计平均值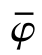
-和φ′，且湍流参数的瞬时值等于平均值与脉动值的线性叠加，即
内燃机整个工作循环中，其缸内气体充量始终进行复杂而又强烈瞬变的湍流运动。湍流的重要特点是物理量的脉动，目前描述湍流流动的数值模拟方法主要包括直接数值模拟、大涡模拟和分离涡模拟等。直接数值模拟和大涡模拟的计算时间成本过高，造成资源的浪费。分离涡模拟方法是将大涡模拟和雷诺平均方法结合，在壁面处采用分离涡模拟方法（DES），在湍流的核心区域采用大涡模拟方法（LES）。在大涡模拟计算中，壁面处采用LES方法几乎会占用一半的计算时间。考虑到计算量的问题，分离涡模拟方法是非常合适的选择。分离涡方法将随机变化的湍流瞬时量分解为统计平均值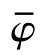
-和φ′，且湍流参数的瞬时值等于平均值与脉动值的线性叠加，即
分离涡模拟方法基于雷诺平均方法中的单方程模型Spalart-Allmaras模型构建[3]，其采用了统一的模型，雷诺平均方法模拟（RANS）与大涡模拟方法模拟区域的切换采用非区域化渐变模式。
在延迟分离涡模型（IDDES）中，对亚网格长度尺度进行了重新定义。模型考虑了网格的各向异性，且调整亚网格长度尺度来实现RANS向LES的过渡。调整后的亚格尺度长度Δ为
分离涡模拟方法基于雷诺平均方法中的单方程模型Spalart-Allmaras模型构建[3]，其采用了统一的模型，雷诺平均方法模拟（RANS）与大涡模拟方法模拟区域的切换采用非区域化渐变模式。
在延迟分离涡模型（IDDES）中，对亚网格长度尺度进行了重新定义。模型考虑了网格的各向异性，且调整亚网格长度尺度来实现RANS向LES的过渡。调整后的亚格尺度长度Δ为
式中，dw为到壁面的距离；hwn为近壁法向网格尺寸；Cw为经验常数，对于附着流动，其取值0.15；hmax=max｛hx，hy，hz｝为非近壁区网格三方向尺寸的最大值。
调整后的亚网格长度尺度Δ沿壁面方向有两种增长方式，第一种是当壁面距离大于近壁法向网格尺寸时，Δ取为定值；随后随壁面距离呈现线性增长的规律，直至壁面距离达到非近壁区网格尺寸，这时亚网格长度尺度过渡到非近壁区网格尺寸hmax。另一种为近壁网格法，法向尺寸的增长率较大时，在线性增长阶段，Δ以更高的增长率变化。
调整后的亚网格长度尺度减小，且在合理的范围内设定了一个陡峭的变化率，这样可以准确模拟RANS到LES过渡区的流动失稳现象。
基于前面的描述，可知IDDES既适合于大尺度分离的模拟，又适合附着流动（WMLES）模拟。对于模拟大尺度分离，重新定义的IDDES可写为
式中，dw为到壁面的距离；hwn为近壁法向网格尺寸；Cw为经验常数，对于附着流动，其取值0.15；hmax=max｛hx，hy，hz｝为非近壁区网格三方向尺寸的最大值。
调整后的亚网格长度尺度Δ沿壁面方向有两种增长方式，第一种是当壁面距离大于近壁法向网格尺寸时，Δ取为定值；随后随壁面距离呈现线性增长的规律，直至壁面距离达到非近壁区网格尺寸，这时亚网格长度尺度过渡到非近壁区网格尺寸hmax。另一种为近壁网格法，法向尺寸的增长率较大时，在线性增长阶段，Δ以更高的增长率变化。
调整后的亚网格长度尺度减小，且在合理的范围内设定了一个陡峭的变化率，这样可以准确模拟RANS到LES过渡区的流动失稳现象。
基于前面的描述，可知IDDES既适合于大尺度分离的模拟，又适合附着流动（WMLES）模拟。对于模拟大尺度分离，重新定义的IDDES可写为
式中，lRANS为RANS 层面的求解尺度，用Spalart-Allmaras 单方程模型时，lRANS=dw；当用k-ωSST模型时，lRANS=k1/2/（Cμω）。
LES 层面的求解尺lLES定义为lLES=CsΨΔ，其中，Ψ为低雷诺数修正函数，可写为
式中，lRANS为RANS 层面的求解尺度，用Spalart-Allmaras 单方程模型时，lRANS=dw；当用k-ωSST模型时，lRANS=k1/2/（Cμω）。
LES 层面的求解尺lLES定义为lLES=CsΨΔ，其中，Ψ为低雷诺数修正函数，可写为
在大多数情况下，忽略式中的ft2，上式可写为
在大多数情况下，忽略式中的ft2，上式可写为(https://www.chuimin.cn)
对于附着流动的模拟，求解尺度定义为
对于附着流动的模拟，求解尺度定义为
fb函数起到调控RANS和LES区域的作用，可写为
fb函数起到调控RANS和LES区域的作用，可写为
fb保证模型从RANS到LES模式的快速切换。
除此之外，为解决近壁雷诺应力估计不足的问题，IDDES模型中增加新项fe。fe主要用于近壁区域，可写为
fb保证模型从RANS到LES模式的快速切换。
除此之外，为解决近壁雷诺应力估计不足的问题，IDDES模型中增加新项fe。fe主要用于近壁区域，可写为
式中，Ψ为经验性修正系数，以保证fe在近壁区发挥出一定效果。
使用统一形式调配WMLES和DDES在流场中的分配[4]，为了进行设置，需将RANS/LES 开关重新定义：
式中，Ψ为经验性修正系数，以保证fe在近壁区发挥出一定效果。
使用统一形式调配WMLES和DDES在流场中的分配[4]，为了进行设置，需将RANS/LES 开关重新定义：
式中，
作为混合RANS/LES方法的一种，DES网格设计以及求解的复杂度比分离技术低很多[5]，对边界层的判断也更加动态化，既可增加灵活性，又可减少计算网格的负担。此外，DES在模拟中的稳定性、持续性很好，且对不同的数值离散精度和离散方法都有相应的裕度。
在小型转子发动机的模拟中，既有大尺度的分离也有附着流动，IDDES-SST方法正好满足气流运动模拟的需求，因此后续的模拟中将采用IDDES-SST 湍流模型。
式中，
作为混合RANS/LES方法的一种，DES网格设计以及求解的复杂度比分离技术低很多[5]，对边界层的判断也更加动态化，既可增加灵活性，又可减少计算网格的负担。此外，DES在模拟中的稳定性、持续性很好，且对不同的数值离散精度和离散方法都有相应的裕度。
在小型转子发动机的模拟中，既有大尺度的分离也有附着流动，IDDES-SST方法正好满足气流运动模拟的需求，因此后续的模拟中将采用IDDES-SST 湍流模型。
相关文章
- 详细阅读
-
多模型耦合全过程模拟泥沙输移问题的流域级研究详细阅读
对于大范围的水土流失与泥沙问题的研究，目前的进展主要有两个方面，一是利用遥感技术进行水土流失调查，二是长河道水沙输移数值模拟。如何在大范围内进行泥沙的产生与输移的多模型耦合全过程模拟，目前鲜有学者提出。“流域”一方面指研究的范围是全流域级的，另一方面指要研究的对象包括坡面、沟道及河道在内的流域总体，而不是仅偏重其中的一部分。......
2025-09-29
-
数值模拟结果分析与讨论详细阅读
观察图7可以发现，Path2 分布着压应力与拉应力两种残余应力形式，在0～0.3 mm 的路径范围内，残余应力形式为拉应力，在0.3～4.4 mm 的路径范围内，残余应力形式为压应力，残余压应力占据了更多的路径区间；在距离路径起始点0.22 mm 与0.44 mm 的位置，存在着与路径其他区域相比更大的残余应力突变，这些应力突......
2025-09-29
-
岸滩侧蚀数值模拟的关键技术详细阅读
由此实现了由岸滩坍塌引起边坡后退过程的模拟。图6.2-4垂向网格跟踪示意图6.2.2.3 垂向网格跟踪技术应用——岸滩侧蚀沿垂向差异特征及其水动力响应采用连续弯道对岸滩侧蚀沿垂向的差异特征及其水动力响应进行概化模拟分析。......
2025-09-29
-
基于数值模拟的离心泵压力脉动特性分析详细阅读
本章基于改进的质量输运空化模型及RNG k-湍流模型，对不同流量工况下离心泵非定常流动进行数值计算，并对非空化工况、空化工况下离心泵叶轮和蜗壳内不同监测点的压力脉动特性进行分析，为离心泵的稳定运行提供一定的参考。离心泵非定常流动数值计算中，小流量下选取非空化工况、NPSHa=1.05m和NPSHa=0.9m；设计流量下选取非空化工况、NPSHa=2.0m和NPSHa=1.8m，非定常计算总时长为10个叶轮周期，叶轮和蜗壳内各监测点压力脉动通过快速傅里叶变换取得频域特性。......
2025-09-29
-
动作研究及其原则详细阅读
动作研究也称为操作法研究。要素动作 简称“动素”，是指构成操作内容的主要动作。对动素继续分析，可找出最小动作。动作观察法 有直接观察法和电视观察法。直接观察法，是在操作现场用眼观察，并用马表或时间测定器记录各动素占用的时间。经过动作研究，得出经济动作的基本原则如下：1）两手同向或同时动作，并尽可能缩小动作。6）尽量避免身体移动、做非自然的动作。......
2025-09-29
-
数值模型验证：探索真实性详细阅读
Ccond=0.000 1时小流量和设计流量工况下离心泵扬程随有效空化余量变化的非定常数值计算结果与试验结果的比较如图2.6所示。表2.2NPSHc计算值与试验结果的比较在本书的离心泵空化流动数值模拟中，质量输运空化模型的凝结项经验系数取0.000 1进行数值计算。图2.7列出了小流量下NPSHa=1.0m和设计流量下NPSHa=1.6m时，3个不同凝结项经验系数所对应的叶轮内空泡体积率分布。......
2025-09-29
-
优化载荷子输运模型的研究详细阅读
单极电荷的输运的数学公式已经被提出。目前，仍未出现同时考虑双极电流、输入受限输运和整体受限输运的统一模型。空穴输运在低能级上完成，所以空穴对因氧气等环境因素而产生的陷阱不敏感。相反，电子对距离较近的这类陷阱敏感并总是表现出弥散输运行为。该理论对OLED的输运描述而言是有价值的。同时，其他研究小组保留了SCLC理论的有效性，并且将迁移率与电场的关系包含在内，这种关系目前是强制性的。......
2025-09-29
相关推荐