首页理论教育建立小型转子发动机微型化数学模型

建立小型转子发动机微型化数学模型

2023-06-23 理论教育版权反馈

【摘要】：为了探究转子发动机微型化极限，本节建立了描述发动机工作过程的简化数学模型。图5.15所示为转子发动机结构示意图。本节热力学模型中的传热模型与5.1.3节相同，重点对气体泄漏模型进行修改。当转子发动机微型化后，发动机内的泄漏路径主要有两个：密封片顶端与气缸内壁面的间隙和转子侧面与端盖内侧的间隙。

为了探究转子发动机微型化极限，本节建立了描述发动机工作过程的简化数学模型。图5.15所示为转子发动机结构示意图。为了简化数学模型及避免相关性不高的因素干扰，本节做了以下假设：

（1）燃烧过程为等容过程；

（2）新鲜充量和燃烧产物都为理想气体，比热值为定值；

（3）密封片与气缸内壁面的间隙和转子侧面与端盖间的间隙为定值；

（4）气体通过泄漏间隙是一维稳态可压缩的过程；

（5）忽略机械摩擦损失。

本节热力学模型中的传热模型与5.1.3节相同，重点对气体泄漏模型进行修改。当转子发动机微型化后，发动机内的泄漏路径主要有两个：密封片顶端与气缸内壁面的间隙和转子侧面与端盖内侧的间隙。下面将对这两种泄漏路径的数学模型进行详细推导。

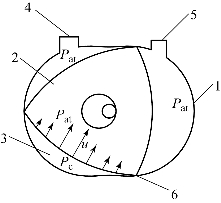
pagenumber_ebook=155,pagenumber_book=145

图5.15　转子发动机结构示意图

1—气缸；2—转子；3—燃烧室；4—进气口；5—出气口；6—密封片

1.通过密封片顶端的气体泄漏

图5.16所示为密封片顶端气体泄漏示意图。笛卡儿坐标系固定在气缸壁面。

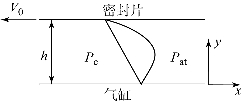
pagenumber_ebook=156,pagenumber_book=146

图5.16　密封片顶端气体泄漏示意图

模型中的假设总结如下[8]：

（1）密封片相对于气气缸壁面是一个移动的半无限平面，因此P/y≈0；

（2）泄漏通道内的气体黏度为空气黏度；

（3）泄漏通道内为层流气体。

根据以上假设对Navier-Stokes方程进行简化可得

方程（5.41）的边界条件为u（0）=0和u（h）=V0，通过分离变量法求解此微分方程可得

由式（5.42）可求得平均速度

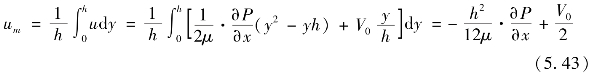
pagenumber_ebook=156,pagenumber_book=146

式中，μ为气体黏度；P和u分别为气体压力和x方向的速度分量；h为泄漏间高度。式（5.43）包含两部分：压力梯度引起的气体流量和密封片移动引起的气体流量。通过估算，在转速为40 000r/min，泄漏间隙为10μm时，密封片移动引起的泄漏量仅为压力梯度引起的泄漏量的0.04%，因此后面计算中密封片移动引起的泄漏被忽略。质量流量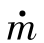 pagenumber_ebook=156,pagenumber_book=146 为

由于泄漏间隙内的高压力梯度，通过泄漏间隙的气体被认为可压缩气流。可压缩雷诺方程为

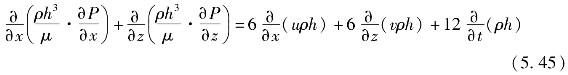
pagenumber_ebook=156,pagenumber_book=146

式中，ρ为气体密度；v为y方向的速度分量。基于稳态假设和对称假设，可得ρh/t=0，v=0，/z=0，同时忽略密封片移动引起的泄漏，雷诺方程可简化为

泄漏间隙内的充量温度随着压力降低而升高，这种变化可显著影响泄漏流量。由于压力降低引起的气体温度升高由以下公式表征：

式中，T为泄漏气体的温度；cp为气体比热。由式（5.46）、式（5.47）和理想气体方程，通过一次积分和二次积分可得

pagenumber_ebook=157,pagenumber_book=147

结合边界条件Px=0=Pc，Px=Lat=Pat（Lat为泄漏路径的长度，Pat为大气压力），可以解得C1，进而得到

pagenumber_ebook=157,pagenumber_book=147

2.通过转子侧面的气体泄漏

如图5.17所示，笛卡儿坐标系固定在转子表面，气体泄漏路径在靠近转子顶端附近的长度比较短，因此泄漏路径的长度的分布假设为抛物线形。抛物线由以下公式给出：

pagenumber_ebook=157,pagenumber_book=147

图5.17　转子侧面的气体泄漏示意图

通过转子侧面的气体泄漏速度为

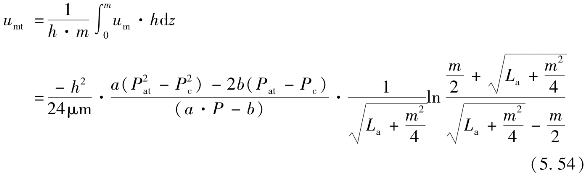
pagenumber_ebook=158,pagenumber_book=148

泄漏气体质量速率为

pagenumber_ebook=158,pagenumber_book=148

3.堵塞流

当发动机燃烧室内处于燃烧及膨胀过程，缸内压力剧增，使得泄漏流速达到当地声速。本节认为当泄漏出口的平均速度达到出口压力将高于大气压力，其值可由式（5.42）、式（5.47）、式（5.52）和理想气体方程联立求解：

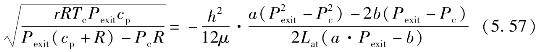
pagenumber_ebook=158,pagenumber_book=148