首页理论教育建立仿真模型的子模块：优化方案

建立仿真模型的子模块：优化方案

2023-06-23 理论教育版权反馈

【摘要】：图5.2所示为本次仿真使用的偏心轴转角子模型。具体的方法已在5.1.2节中详述，此处MATLAB/Simulink模型将式和式整合，并表达成图5.4所示模型进行计算：图5.2偏心轴转角子模型2.工作室容积子模型转子发动机在工作时，工作室容积变化规律如式（5.9）所示，在发动机基本参数确定之后，它仅是偏心轴转角的函数。

1.偏心轴转角子模型

MATLAB/Simulink等软件中直接运行的自变量为“仿真时间”，然而在转子发动机的各运行参数中，最直接的自变量却是“偏心轴转角”。偏心轴转角是一个角度参量，跟时间不一样，它有一定的重复性，可以实现转子发动机的多个循环或者多个工作状态仿真。实现偏心轴转角与仿真时间的对应关系，对于各参量的施加都有十分现实的意义。

图5.2所示为本次仿真使用的偏心轴转角子模型。n为偏心轴转速偏心轴转角与仿真时间的关系可以表达为

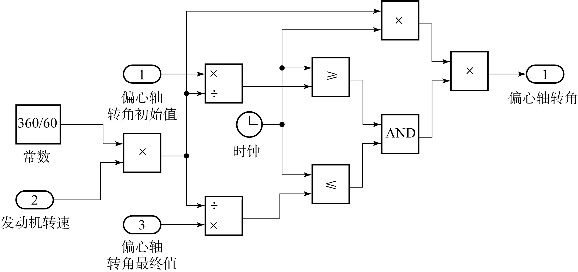
pagenumber_ebook=141,pagenumber_book=131

图5.2　偏心轴转角子模型

2.工作室容积子模型

转子发动机在工作时，工作室容积变化规律如式（5.9）所示，在发动机基本参数确定之后，它仅是偏心轴转角的函数。在MATLAB/Simulink中将函数表达式通过图形化编程语言进行表示，搭建工作室容积子模型，如图5.3所示。

3.漏气简化子模型

漏气模型在整个零维模型中起到对所有过程工质质量M的修正。考虑漏气的零维模型会将各个阶段泄漏的工质质量从总质量中去除。具体的方法已在5.1.2节中详述，此处MATLAB/Simulink模型将式（5.23）和式（5.24）整合，并表达成图5.4所示模型进行计算：

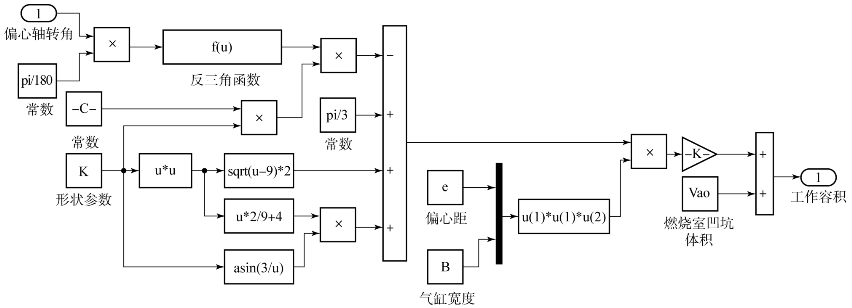
pagenumber_ebook=142,pagenumber_book=132

图5.3　工作室容积子模型

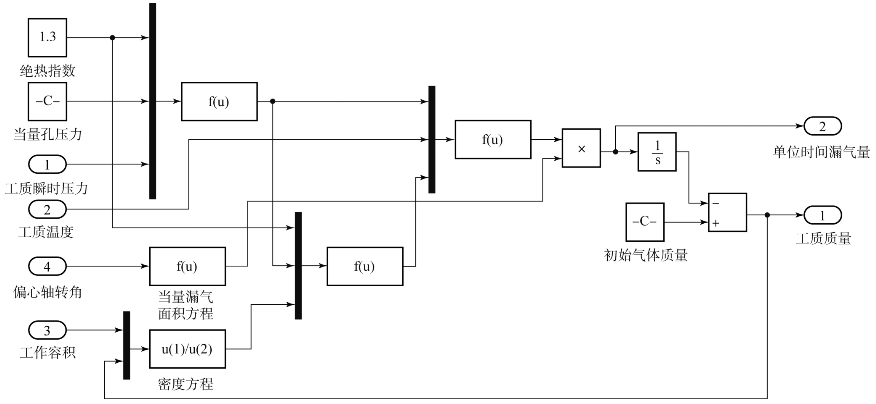
pagenumber_ebook=143,pagenumber_book=133

图5.4　漏气简化子模型

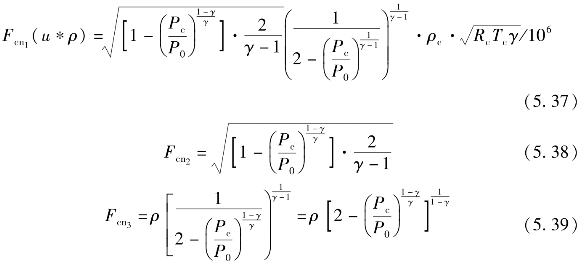
pagenumber_ebook=144,pagenumber_book=134

“Aeff“表示当量漏气面积，与“Fcn1“相乘所表达的含义如式（5.24）所示，相乘所得的结果为单位时间漏气量 pagenumber_ebook=144,pagenumber_book=134 。实际上，经过图5.3中漏气简化子模型的处理，可以得到泄漏通量随仿真时间的变化规律。

4.传热子模型

根据式（5.25）建立MATLAB/Simulink传热子模型，如图5.5所示。

pagenumber_ebook=144,pagenumber_book=134

图5.5　传热子模型

需要指出的是，在MATLAB/Simulink仿真过程中，具有实际意义的热量损失的变化规律是而并非因此用式（5.40）来进行转化：

图5.5所示的传热子模型中还包含有一个“传热系数“子模型，如图5.6所示。传热系数通常情况下无法直接获取，零维仿真模型采用经验公式法将其引入传热模型中。

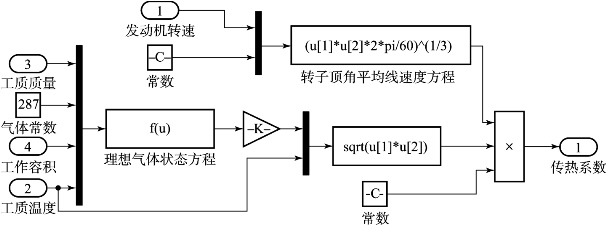
pagenumber_ebook=145,pagenumber_book=135

图5.6　传热系数子模型

5.压力子模型

在气缸内各阶段热力过程数学建模中，存在项压力子模型便是用来计算该项的模型，如图5.7所示。

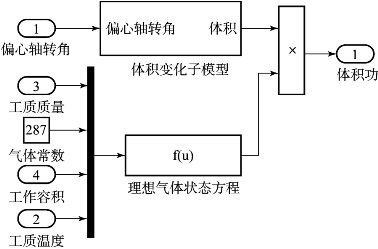
pagenumber_ebook=145,pagenumber_book=135

图5.7　压力子模型

在气缸内各阶段热力学过程中，气体状态方程（5.3）均成立，因此缸内工质的瞬时压力Pc可以由工质的质量M、气体常数Rc、工质温度Tc及此时的工作容积V计算得出。而只能通过构建子模型来计算，如图5.8所示。

pagenumber_ebook=146,pagenumber_book=136

图5.8　d V/dφ子模型

该子模型中采用的公式如式（5.11）所示。

6.放热子模型

实际缸内燃烧放热过程非常复杂，在仿真过程中通常选用简化的燃烧放热规律代替实际的放热过程。目前，最常用的放热模型为韦伯燃烧模型，其表达式如式（5.29）所示。在Simulink中搭建的燃烧放热子模型如图5.9所示。