气缸内各阶段热力过程的数学建模优化提示

2023-06-23 理论教育版权反馈

【摘要】：图5.1所示为转子发动机气缸内工质与外界进行质量和能量交换的示意图。实际工作过程中，小型转子发动机要经历四个冲程，四个冲程内的热力学过程不同。缸内热力学过程的计算主要依据各阶段热力过程工质状态变化规律及能量转换情况进行。在进行热力学仿真之前，需要先将转子发动机的运动学规律用数学公式表达出来，以便在发动机气缸内各热力学阶段仿真时使用。

将小型转子发动机物理模型划分为三个子系统：进气子系统、排气子系统和气缸子系统。其中气缸子系统与排气子系统、进气子系统相连，由气缸的内包络面、转子外包络面、前后端盖组成。径向密封片及弹簧对子系统体积影响极小，故此处忽略它们所占体积的影响。

将这三个子系统做零维假设：①子系统内各参数不随空间坐标而变化；②子系统内各点的状态参数、工质成分相同；③子系统各参数只随偏心轴转角变化；④各子系统之间存在质量、能量交换；⑤各子系统之间的工质流动视为稳定流动。依据热力学工况，建立子系统的能量守恒方程、质量守恒方程和理想气体状态方程。

图5.1所示为转子发动机气缸内工质与外界进行质量和能量交换的示意图。电热塞有较高的热值，能够点燃可燃的高压混合气体。在进行燃烧室内热力过程模拟时，所做的基本假设和传统的往复式活塞发动机相同，即：

（1）气缸内的状态是均匀的。即不考虑气缸内各点的压力、温度和组分的差异，并认为在进气期间，流入气缸内的空气与缸内残余废气实现瞬时的完全混合。

（2）工质为理想气体。其比热、比内能和比焓仅与气体温度和成分有关。

（3）燃料燃烧释放化学能的过程，假设为外界按已知的放热表观规律向系统内工质加热的热力学过程。

（4）忽略工质进、出口处的流体的动能。

pagenumber_ebook=132,pagenumber_book=122

图5.1　燃烧室内热力系统示意图

依据上述假设、能量守恒定律、质量守恒定律和理想气体状态方程，建立燃烧室内的能量守恒方程组如下：

pagenumber_ebook=132,pagenumber_book=122

式中，为气缸工质内能的变化；为吸入燃油释放的热量；hin为吸入新鲜空气带入的热量；为排出废气带走的热量；hcrev为室内工质与缝隙体积内气体交换的热量；为漏气所带走的热量；为室内气体与前后端盖、气缸壁面所交换的热量；为气体对三角转子所做的机械功。

得出燃烧室内工质的质量守恒方程为

式中，为气缸内工质质量的变化；为进入气缸内工质的质量；为排出气缸外的工质的质量；为漏气的质量；为缝隙体积质量；为加入气缸内燃油的质量。

理想气体的状态方程为

式中，P为气体压强；V为气体体积；m为气体质量；R为理想气体常数；T为气体温度。系统内的比内能和质量通常是同时随偏心轴转角的变化而变化，因而可得

针对小型转子发动机，可将内能简化为温度和瞬时过量空气系数的函数，即

故而可以得出内能随着偏心轴转角的变化方程如下：

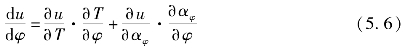
pagenumber_ebook=133,pagenumber_book=123

而

将式（5.3）、式（5.6）、式（5.7）代入式（5.1）即可得到温度对偏心轴转角的偏微分方程：

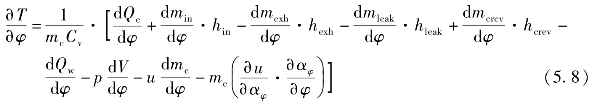
pagenumber_ebook=133,pagenumber_book=123

式（5.8）描述了小型转子发动机的内部温度随偏心轴转角变化的规律，它是描述发动机缸内工作过程最基本的微分方程，是适用于小型转子发动机缸内工作过程的通用微分方程。实际工作过程中，小型转子发动机要经历四个冲程，四个冲程内的热力学过程不同。本章将把小型转子发动机的四个工作过程分开进行研究和计算，可减少计算量，提高准确性。

缸内热力学过程的计算主要依据各阶段热力过程工质状态变化规律及能量转换情况进行。依据热力学过程可将小型转子发动机的工作过程分为进气-压缩-燃烧-膨胀-排气-进排气重叠六个部分[1]。小型转子发动机的工作特点使得偏心轴需要经历1 080°才能完成一个工作循环，在这个工作循环中上述六个过程每个工作室均发生一次。对上述六个过程分别求解，即可得出所研究工作室内的压力、温度等随偏心轴转角的变化规律。那么，与所研究工作室相邻前后两工作室内工质的压力、温度分别为P（φ+360°）、T（φ+360°）和P（φ+720°）、T（φ+720°）。

在进行热力学仿真之前，需要先将转子发动机的运动学规律用数学公式表达出来，以便在发动机气缸内各热力学阶段仿真时使用。

转子发动机在工作时体积的变化规律为

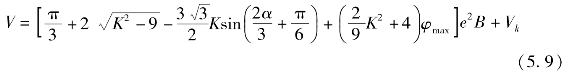
pagenumber_ebook=134,pagenumber_book=124

式中，K=R/e为小型转子发动机的形状参数；e为偏心距；φmax为最大摆动角；α为偏心轴转角[此处需声明，在转子发动机的几何学中，定义α=0对应于偏心轴轴心到偏心盘圆心的方向向量与x轴正方向（水平方向）重合的时刻，但是为了描述方便，在转子发动机性能计算中取φ角作为偏心轴转角的计量符号，并有φ=α+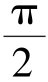 pagenumber_ebook=134,pagenumber_book=124 π，即φ=0对应于转子发动机进排气重叠的换气过程]；B为气缸宽度；Vk为单个转子凹坑体积。

那么，瞬时气缸容积的变化率为

若使用φ角表示，则

1.压缩期热力学建模

压缩期为转子某个工作面后方径向密封片扫过进气口，结束了进气环节，至压缩至上点之前的过程所对应的偏心轴转角。在仿真计算中，简化为某个工作室容积从最大的时刻到最小的时刻所对应的偏心轴转角：

式中，为转子发动机理论进气时刻角。压缩期燃烧室处于相对独立的状态，除了漏气和上个工作室在火花塞（电热塞）凹坑的缝隙内残余的废气质量会使缸内质量变化以外，不存在其他质量的摄入、消耗。即

则，质量守恒方程（5.2）可以简化为

pagenumber_ebook=135,pagenumber_book=125

式中，

式中，mL为缸内气体的质量，包括上一循环残余废气中的空气量；mfr为由上一循环缸内残余废气所折算的燃油质量。

由能量守恒方程（5.1）推算的缸内温度随偏心轴转角变化方程（5.8）可以简化为

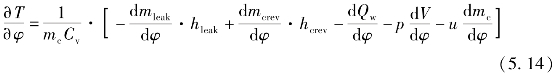
pagenumber_ebook=135,pagenumber_book=125

2.燃烧膨胀期热力学建模

由于燃烧所用时间较短且与膨胀同时发生，实际上燃烧和膨胀环节合在一起就是通常意义上的“做功冲程”，所以本节将燃烧和膨胀时期过程同时计算，对应偏心轴转角上的结果进行累加。

膨胀期所对应的偏心轴转角范围：

式中，为转子发动机理论排气时刻角。燃烧期所对应的偏心轴转角及燃烧本身的参数在燃烧放热模型部分会详细介绍，此处不做赘述。

在燃烧和膨胀时期，没有新鲜工质的进入，也没有废气的排出，同时本计算对象为化油器式转子发动机，燃料的摄入在进气环节完成，故有

燃烧膨胀期存在漏气现象，基于零维模型假设，可以认为转子发动机在热力学计算模型中不存在燃油泄漏问题。另外，膨胀过程后期，转子在其运动方向的后方密封片扫过火花塞（电热塞）孔时，残留在孔内、孔下缝隙容积内的高温高压气体会进入下一工作室，对于本工作室来说则为质量损失，故燃烧和膨胀期间的质量守恒方程可以简化为

要计算缸内工质的变化，必须了解缸内的燃料质量变化规律。依据上述假设将燃烧过程视为按已知的放热表现规律向缸内工质的加热过程，此处将放热表现规律视为当量燃烧规律，依据此假设忽略了着火延迟期内缸内工质质量的变化。燃烧过程视为理想过程，燃烧后缸内燃料的质量视为零。

则燃烧期能量方程可以简化为

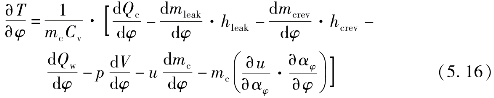
pagenumber_ebook=136,pagenumber_book=126

在膨胀过程中，缸内工质质量变化是由漏气和间隙引起的。此时aφ值，即燃烧终了时刻的值不发生变化。此期间能量方程为

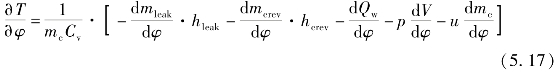
pagenumber_ebook=136,pagenumber_book=126

3.排气期热力学建模

排气阶段，气缸内无燃烧反应，此时燃烧释放的热量恒为零，不再发生变化。而且从进气、排气过程进出气缸内气体的质量恒为零，但是该过程系统通过边界向外界传递能量和质量。在排气过程中的质量和能量通用微分方程为

在排气阶段，无气体流入气缸，但有废气排出气缸，气体成分不变，即dαφ/dφ=0，dmin/dφ=0，dmexh/dφ≠0。故此阶段的能量微分方程为

pagenumber_ebook=136,pagenumber_book=126

4.进气期热力学分析

在进气和燃料混合阶段，新鲜空气的流入量dmin/dφ≠0，排气量dmexh/dφ=0，但进入气缸内的燃油质量dmfuel/dφ≠0，因此该阶段的质量方程为

燃料的摄入量依据其燃空当量比恒为理想比例的情况下摄入，所以

式中，L为实际空气量；H为气缸截面厚度；V为工作室容积。此阶段的能量方程为

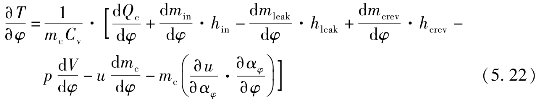
pagenumber_ebook=137,pagenumber_book=127

以上各阶段的能量和质量方程中，dmin/dφ，dmexh/dφ，dmleak/dφ，dmcrev/dφ，dmfuel/dφ，dQc/dφ，dmin/dφ，dmexh/dφ，dmleak/dφ，dmcrev/dφ，d Qw/dφ，dmc/dφ，u/αφ，αφ/φ是边界条件需要提供的微分变量，是求解微分方程的边界条件。对能量方程求解，可以得出温度随偏心轴转角的变化规律；对质量方程求解，可以得到缸内工质质量随偏心轴转角的变化规律；对理想气体的状态方程求解，可以得出缸内压力随偏心轴转角的变化规律。

气缸内各阶段热力过程的数学建模优化提示

相关推荐