可采用有限元柔性体方法，使用有限元软件ANSYS生成包含构件几何、质量和模态信息的模态中性文件，再通过ADAMS/Flex接口读入ADAMS/View中建立柔性体，进而得到断路器的刚柔耦合混合动力学模型。在ADAMS软件中设置柔性体的参数并添加相关约束，可以得到框架断路器的刚柔耦合混合动力学模型。由于框架断路器机构复杂，零部件很多，因此仿真中分别以上连杆、打击杆和轴销为柔性体建立框架断路器的刚柔耦合分析模型，如图3-5所示。......
2023-06-15
建立径向密封片混合润滑模型
【摘要】：为了防止高压燃烧室向相邻燃烧室漏气，小型转子发动机设计有径向密封片。径向密封片底部安装径向预紧弹簧以提供预紧力。径向密封片与气缸之间紧密接触以保证燃烧室的径向密封。工作情况下，径向密封片沿着气缸内壁高速滑动，径向密封片和气缸之间油膜力可根据雷诺方程求得。
与常规尺寸的转子发动机相比，少量漏气会导致小型转子发动机输出功率大幅下降。小型转子发动机三个燃烧室内部气体压力交替变化。为了防止高压燃烧室向相邻燃烧室漏气，小型转子发动机设计有径向密封片。径向密封片底部安装径向预紧弹簧以提供预紧力。对小型转子发动机截面进行扫描，获得截面扫描图如图4.3（a）所示，径向密封片和气缸的接触示意图如图4.3（b）所示。
图4.3（b）中ηO3ξ为运动坐标系，O3为密封片顶部圆弧圆心，ξ轴与密封片径向方向平行，η轴与密封片纵向方向平行，β为运动坐标系和大地坐标系xOy夹角，O为气缸形心，Ox 平行于气缸型线长轴，Oy 平行于气缸型线短轴。工作过程中，转子发动机三个燃烧室依次经历进气、压缩、点火、膨胀和排气。径向密封片与气缸之间紧密接触以保证燃烧室的径向密封。在工作过程中，径向密封片在径向上受到背部弹簧预紧力、底部气体压力、惯性力、顶部气体压力。混合润滑情况下径向密封片受力示意图如图4.4所示。
图4.3 结构示意图
（a）转子发动机截面扫描图；（b）径向密封片与气缸接触示意图
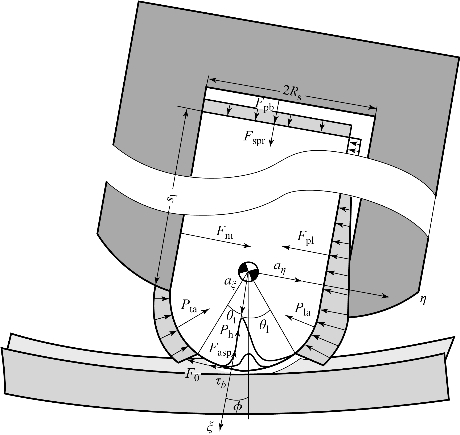
图4.4 混合润滑情况下径向密封片受力示意图
此时，径向密封片的径向平衡方程为
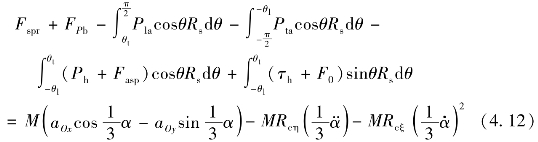
式中，Fspr为弹簧预紧力；Fpb为底部气体载荷；Pla为引导燃烧室内气体压力；Pta为跟随燃烧室内气体压力；Fasp为微凸体接触压力；F0为微凸体摩擦力；Rs为密封片顶部圆弧半径；M为密封片质量；Ph为密封片与气缸之间的油膜压力；τh为油膜切向力；θl和θt为油膜分别在引导侧和跟随侧的浸润角度；Rcη和Rcξ为密封片质心在ηO3x坐标系中的坐标；aOx和aOy为O3点在大地坐标系下沿x轴和y轴的加速度。其中θl和θt的表达式如下：
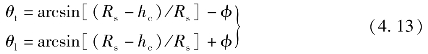
式中，hc为油层厚度；φ为摆动角。aOx和aOy的表达式如下：
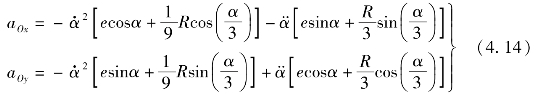
式中，e为偏心距。
工作情况下，径向密封片沿着气缸内壁高速滑动，径向密封片和气缸之间油膜力可根据雷诺方程求得。雷诺方程考虑了流体的动压效应、伸缩效应和挤压效应。在混合润滑时，表面微观形貌会影响两者之间流体压力，如图4.5所示。
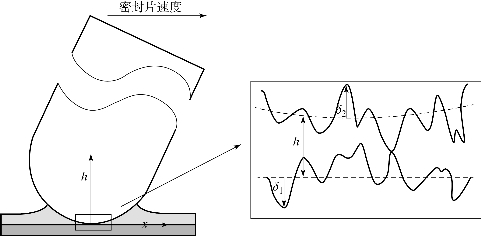
图4.5 考虑粗糙度的两表面之间的油膜厚度示意图
在混合润滑情况下，雷诺方程不再适用。考虑粗糙度对密封片和气缸之间润滑状态的影响，本研究采用Patir和Cheng提出的平均雷诺方程[5]：
式中，h为油膜厚度；φx为压力流量因子；φs为剪切量因子；φc为接触因子；μ为润滑剂黏度；U为密封片相对于气缸速度；σ为综合粗糙度；t为时间。接触因子φc受粗糙度分布影响。基于Wu和Zheng的研究[6]，接触因子如下式所示：
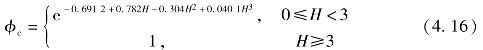
压力流量因子φx也受表面微观形貌参数的影响，压力流量因子需要对微凸体分布函数积分获得，此处平均压力流量因子拟合式为
对上述公式拟合可得出剪切流量因子参数为
式中，A1、A2、α1、α2和α3的取值可参见文献[7]。混合摩擦情况下，微凸体接触模型如前文所述。
有关小型转子发动机数值建模与仿真分析的文章
- 详细阅读
-
径向密封片与气缸摩擦损失分析 -> 气缸摩擦详细阅读
图4.8密封片和气缸之间油膜厚度变化图4.11引导燃烧室和跟随燃烧室内压力混合润滑情况下，径向密封片和气缸之间存在着油膜力和微凸体接触压力，两载荷随偏心轴转角的变化如图4.12所示。图4.13油膜和微凸体引起的摩擦力由图4.13可知，在一个循环内，微凸体摩擦力与微凸体接触力的变化趋势几乎相同，分别在微凸体接触力最大和最小的位置取得最大值和最小值。......
2023-06-23
-
任务9：扫描混合特征建立把手详细阅读
任务描述用扫描混合特征，建立完成如图2-9-1所示的把手。图2-9-1把手任务实施一、新建进入实体建模模块步骤选择“新建”→选择“零件”模块→输入公用名称“2-9-1”→将“使用缺省模板”的钩去掉→单击“确定”，如图2-9-2所示，进入实体建模模块。单击“草绘”按钮，进入把手混合特征轨迹的草绘界面。图2-9-23起始点选取问题任务拓展建立扫描混合特征时，如何做到截面图元数相等是关键，如下例。......
2023-06-15
-
建立综合优化调度评估模型详细阅读
本节将运用赋权重的方法考虑各方面约束，以防洪、发电、航运、泥沙为主要优化目标，建立综合优化调度方案评估模型，为三峡水库选定优化调度方案提供决策支持。......
2023-06-21
-
COMSOLMultiphysics仿真模型详细阅读
COMSOL Multiphysics对于不同案例的具有类似的建模流程，以流体流动模块中的CFD建模为例，可以总结为以下几个步骤。第2步：构建几何模型对于结构比较简单的几何模型，可以采用COMSOL Multiphysics中的“几何”功能模块建立模型；对于结构相对复杂的对象，可以先采用AutoCAD等专业几何设计软件进行设计，再导入COMSOL Multiphysics。对于不太复杂的几何模型，COMSOL Multiphysics近年来的版本都有较好的自适应划分策略。......
2023-11-03
- 详细阅读
-
仿真模型的建立及分析结果详细阅读
图3-25 三角形隶属度函数模糊控制规则是模糊控制的核心，因此，如何建立模糊控制规则成为一个十分关键的问题。根据表3-3所示参数，由式可得D0=0.24；由式可得x0=[0.11573600]T；由式可得图3-28 模糊控制器输出曲线图3-28 模糊控制器输出曲线图3-29 有源电力滤波器整体仿真模型表3-3 仿真参数图3-29 有源电力滤波器整体仿真模型表3-3 仿真参数取正定矩阵取正定矩阵根据实验取定根据实验取定具体仿真结果如下：1）图3-30所示为无滤波器的情况下电网电流波形。......
2023-06-23
-
建立分析模型步骤与实例详细阅读
首先采用梁模型针对简支边界条件建立转子分析模型，并进行计算分析。在Analysis Type下拉列表框中选择临界转速分析Critical SpeedStability。输入第4个点坐标，即X：76.2，Y：0，Z：0。在屏幕上用鼠标捕捉Ponit1～Point18。单击Apply按钮生成一条线。模型数据树如图14-39所示，单击图标可以展开此数据树。......
2023-10-27
相关推荐