用阴极保护法使金属得到完全保护时，必须达到的电位称为最小保护电位。从阴极保护原理可知，最小保护电位就是腐蚀微电池微阳极的平衡电极电位。由于参比电极不同，所测的数值也不同，所以在说明保护电位时，必须指明所用的参比电极。从理论上讲，金属在最小保护电位时的保护效率应为100%，但实际上是不可能的，所以只能把保护效率最高的电位作为最小保护电位。......
2025-09-29
如何确定飞轮的惯量？
【摘要】：当发火不均匀时，需要分析偏心轴输出扭矩曲线在一个周期内循环的变化规律，方可进行飞轮的设计。此外，在转子发动机上安装较大转动惯量的飞轮，也能够减小偏心轴扭矩的不均匀度。在稳定的工况下，扭矩的平均值应等于阻力矩的平均值。由式可以得到在每一指定的瞬时Ms和MQ的差值决定了角加速度的符号。表2.4一些发动机对δ值的要求偏心轴旋转不均匀度δ应限制在一定的范围内。
从偏心轴的输出扭矩图（图2.37）可以看出，小型转子发动机输出扭矩是随着偏心轴转角α的变化而不断变化的。偏心轴旋转的不均匀性，会带来一系列的危害：使小型转子发动机与它带动的从动件之间产生冲击，影响工作可靠性和使用寿命，并产生噪声；使偏心轴振动；使监控或测试的仪器工作不稳定等。因此需要有一定的措施来减少转子发动机偏心轴输出的不稳定性。
为了评价小型转子发动机输出扭矩变化的均匀程度，用扭矩不均匀度μ来表示：
式中，Mmax、Mmin分别为偏心轴输出扭矩的最大值和最小值；Mcp为偏心轴输出扭矩的平均值。
对于同一台转子发动机，扭矩的不均匀度随其工况变化而变化，但随缸数的增加，扭矩的不均匀性迅速降低。扭矩的不均匀变化必然会引起转子发动机偏心轴转角速度的波动。为减小这种波动，一般可以采用多缸机的组合方式（多缸机各缸交替做功，发火间隔均匀时，就能保证最佳的扭矩均匀性）。此外，在转子发动机上安装较大转动惯量的飞轮，也能够减小偏心轴扭矩的不均匀度。
对于发火均匀的多缸转子发动机，偏心轴输出扭矩曲线是以发火间隔角ξ为周期循环变化的。实际上只要分析偏心轴输出扭矩在ξ角度范围内的变化规律，就可以掌握偏心轴角速度的变化情况，进而完成飞轮设计。当发火不均匀时，需要分析偏心轴输出扭矩曲线在一个周期内循环的变化规律，方可进行飞轮的设计。
转子发动机的扭矩在任一瞬间，都与加在偏心轴上的阻力矩及所有运动质量的惯性力矩相平衡，并可用下式表示：
式中，Ms为转子发动机输出扭矩的瞬时值；MQ为阻力矩；Io为所有运动件换算到偏心轴上的转动惯量。
在稳定的工况下，扭矩的平均值应等于阻力矩的平均值。由于阻力矩与扭矩的变化周期及变化规律通常并不一致，因此，偏心轴的角速度不可避免地要经常变化。通常认为阻力矩MQ是一个常数，而且等于平均扭矩Mcp，如图2.39所示。
偏心轴角速度的变化取决于Ms和MQ之间的差值。由式（2.21）可以得到
在每一指定的瞬时Ms和MQ的差值决定了角加速度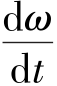
的符号。
当Ms＞MQ时，角加速度为正值，偏心轴的角速度增大；当Ms＜MQ时，角加速度为负值，偏心轴的角加速度减小；当Ms=MQ时，扭矩曲线与代表阻力矩的直线（即Mcp）相交于ABCDGH各点，对应的角加速度为零，此时上述各点的角速度达到瞬时最大值或最小值。在一个运动周期内偏心轴旋转的不均匀程度将取决于ωmax和ωmin的大小。
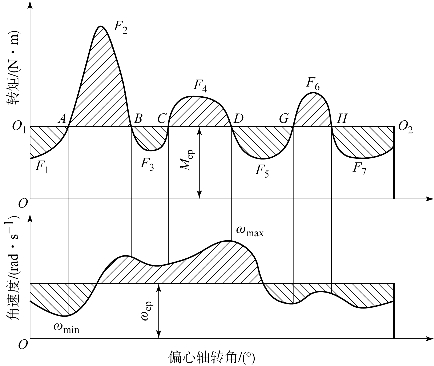
图2.39 稳定工况下的偏心轴角速度示意图
偏心轴的最大角速度与最小角速度之差与平均角速度之比为偏心轴旋转的不均匀度，即(https://www.chuimin.cn)
当δ不大时，可近似地取平均角速度为
式（2.24）代入式（2.23）得到
偏心轴旋转不均匀度δ应限制在一定的范围内。表2.4列出了一些发动机对δ值的要求，可供设计时参考。
表2.4 一些发动机对δ值的要求
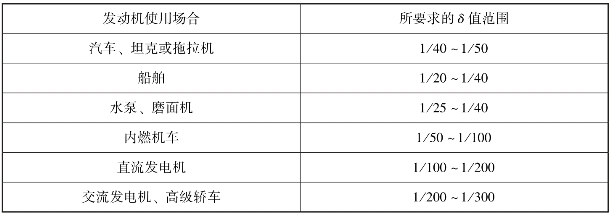
当δ值确定后，可选择具有适当转动惯量IM的飞轮来使之满足要求，具体做法是：
根据图2.39所示偏心轴输出扭矩、转速，求出偏心轴角速度从ωmin变化至ωmax时所对应的偏心轴输出扭矩曲线与阻力矩曲线之间所包围的面积，此面积所代表的功通常称为盈亏功Ws，有
由于物体在任意两个瞬时之间动能的变化等于作用于该物体上的力或力矩在这个过程中所做的功，则有
联立式（2.26）与式（2.27），即可得
Io主要由三部分组成：飞轮的惯量、转子组的转动惯量、偏心轴及平衡重的转动惯量。一般来说，飞轮的惯量IM比其他的转动惯量大得多。对汽车、坦克内燃机来说，IM占总转动惯量的85%～90%，而对拖拉机来说，则占75%～85%。
这样，就可以求出飞轮所需要的转动惯量IM的值。
相关文章
- 详细阅读
-
超静定结构的多余约束个数如何确定详细阅读
超静定结构区别于静定结构的基本特征就是具有多余约束，超静定次数是指超静定结构中多余约束的个数。如果从一个超静定结构中解除n个约束，结构变为静定结构，则原来的超静定结构为n次超静定。如图14-5所示超静定刚架，去掉中间的单铰，以两对未知力X1、X2代替相应的约束，就成为如图14-5所示的静定刚架，故原刚架是两次超静定结构。无论采用何种方式，原结构的超静定次数都是相同的。......
2025-09-29
-
如何确定重载型自动扶梯的额定载荷详细阅读
额定载荷是运输设备最重要的设计参数，需要用于驱动电动机的功率设计和机件的强度设计。重载型自动扶梯一般以100%的制动载荷作为自动扶梯的额定载荷。鉴于0.8的满载系数在大客流的公共交通场所的高峰时段时有出现，因此以制动载荷作为重载型自动扶梯的额定载荷是相对合理的。美国的通用扶梯标准对自动扶梯规定的额定载荷是一个梯级约87kg；但美国的APTA标准对重载型自动扶梯的额定载荷的要求则是通用标准的1.7倍：145kg/梯级或116kg/梯级。......
2025-09-29
-
如何确定兴利库容设计？详细阅读
G4.7.2.1长系列法当水库坝址处有n年长系列来水及用水资料时，对每年进行调节计算，得到n个兴利库容。根据设计保证率p设，查V—p曲线即可求得相应的年调节设计兴利库容Vp。图G4.11兴利库容频率曲线长系列法设计保证率概念明确，资料具备时应采用此法。G4.7.2.2代表年法所谓代表年法，是指选择一个合适的年型作为代表年，以该代表年的来水过程和用水过程进行年调节计算，求得的年调节库容即设计兴利库容。......
2025-09-29
-
确定产能平衡的优化目标函数详细阅读
生产能力平衡主要是力争实现以下优化目标：根据客户需求分析， 使生产计划排程尽可能按照产品权重满足需求的数量。使负荷尽量接近可行的生产能力。在确定能力平衡目标函数之前， 我们先定义关键参数的符号。在产能不足情况下， 会造成订单丢失的风险。通过工厂内部部门间的协同， 提高自身性能从而达到提升产能的最终目的。......
2025-09-29
-
确定切削用量的方法与技巧详细阅读
具体数值应根据机床说明书和切削用量手册，并结合经验而定。使用球头刀进行精加工时，步距的确定应首先考虑所能达到的精度和表面粗糙度。因此，编程人员必须熟悉刀具的选择方法和切削用量的确定原则，从而保证零件的加工质量和加工效率，充分发挥数控机床的优点，提高企业的经济效益和生产水平。......
2025-09-29
- 详细阅读
-
确定液压系统参数的初步步骤详细阅读
系统工作压力p 的确定由于主机的性能和使用场合不同,液压系统的工作压力也不尽相同。因此,系统工作压力的选择取决于尺寸、成本、使用可靠性等多方面因素,一般可参考现有的同类液压系统来初步确定系统工作压力。表8.2常用液压设备工作压力执行元件主要结构参数的确定这里主要确定液压缸的有效工作面积、活塞直径和活塞杆直径,确定液压马达的每转排量。......
2025-09-29
相关推荐