本实例要完成的电容三维实体模型如图9-64所示。图9-64 电容器实体建模实例本实体建模实例的操作步骤如下。使用“三维建模”工作空间，并从功能区“常用”选项卡的“视图”面板中将“真实”视觉样式设置为当前视觉样式。图9-65 绘制圆柱体图9-65 绘制圆柱体图9-66 绘制一个圆环体图9-66 绘制一个圆环体从“布尔值”面板中单击“差集”按钮，选择圆柱体，按
2025-09-29
PSCAD仿真实例演示及优化分析
【摘要】：本节将通过利用高压直流输电系统CIGRE HVDC标准模型及改进模型在PSCAD中的仿真应用，对PSCAD建模和基本仿真过程进行说明。根据原理图可在PSCAD中搭建仿真电路模型，系统仿真模型中主要包括两端交流系统等值电路、换流变压器和阀组等值电路、交流滤波器模型以及变流器控制器设计等。表7-5 交流滤波器参数图7-15 PSCAD主界面图7-16 高压直流输电系统原理图图7-17 主层仿真电路高压直流输电系统逆变侧交流等值系统称为R-L-L型，而整流侧交流等值系统称为R-R-L型。
本节将通过利用高压直流输电系统CIGRE HVDC标准模型及改进模型在PSCAD中的仿真应用，对PSCAD建模和基本仿真过程进行说明。图7-16所示是一个高压直流输电系统的原理图，其中器件数值单位分别是Ω、H和F。根据原理图可在PSCAD中搭建仿真电路模型，系统仿真模型中主要包括两端交流系统等值电路、换流变压器和阀组等值电路、交流滤波器模型以及变流器控制器设计等。整个系统仿真采用模块化设计，主层仿真电路如图7-17所示。
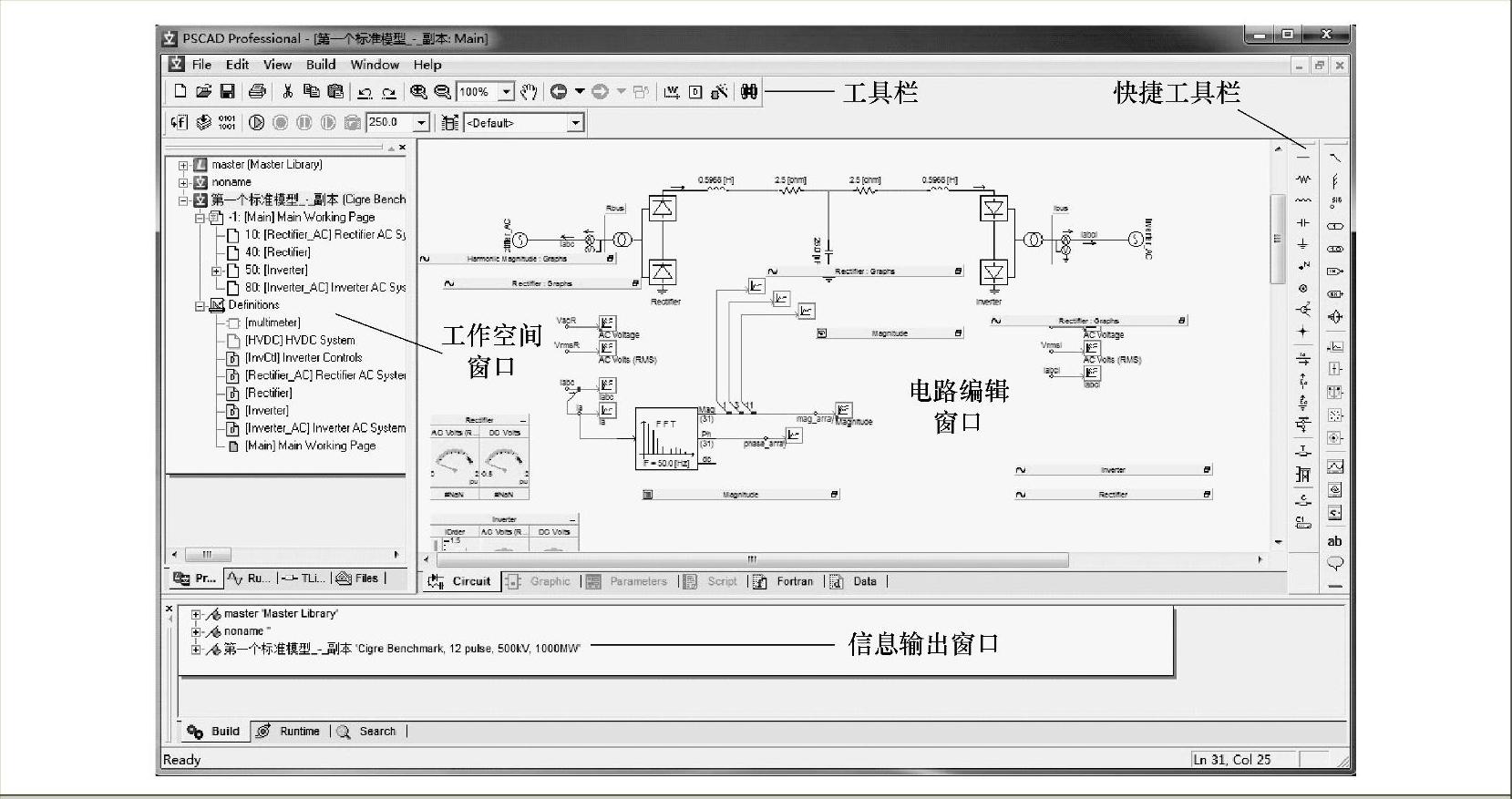
图7-15 PSCAD主界面
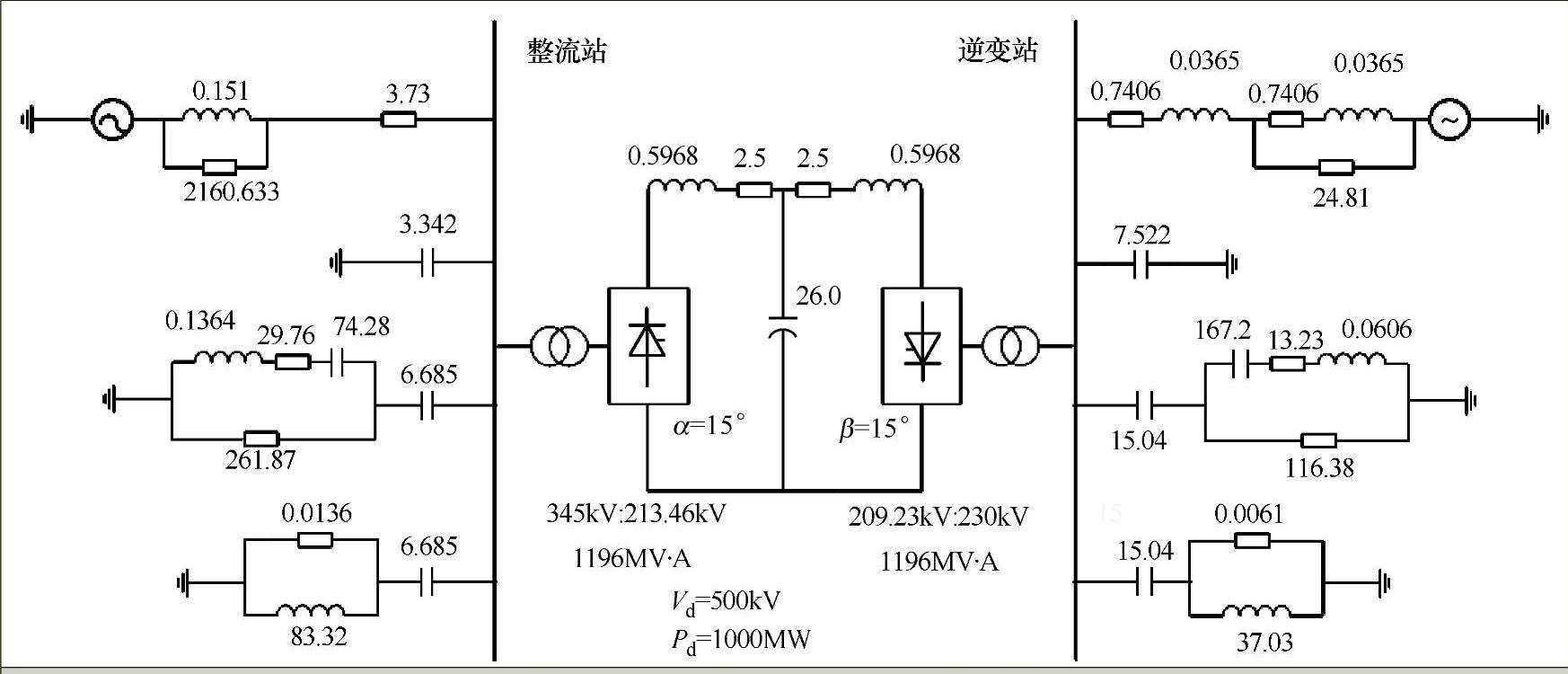
图7-16 高压直流输电系统原理图
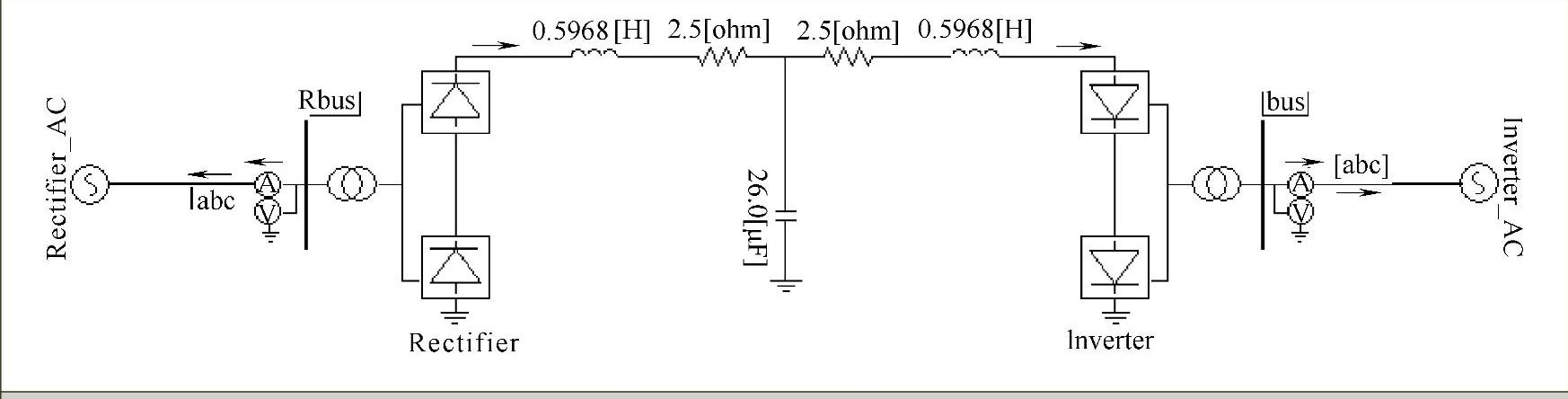
图7-17 主层仿真电路
高压直流输电系统逆变侧交流等值系统称为R-L-L型，而整流侧交流等值系统称为R-R-L型。在低次谐波范围内，这两种等值电路显示了不同的阻抗特性，R-R-L型较容易得到相同的基波和三次谐波阻抗角，R-L-L型则对地侧谐波显示了较高的阻尼。其内部等效电路如图7-18所示，换流变压器和阀组模块内部具体电路见附录A。控制器设计包括整流侧控制器和逆变侧控制器，其控制系统框图见附录B。
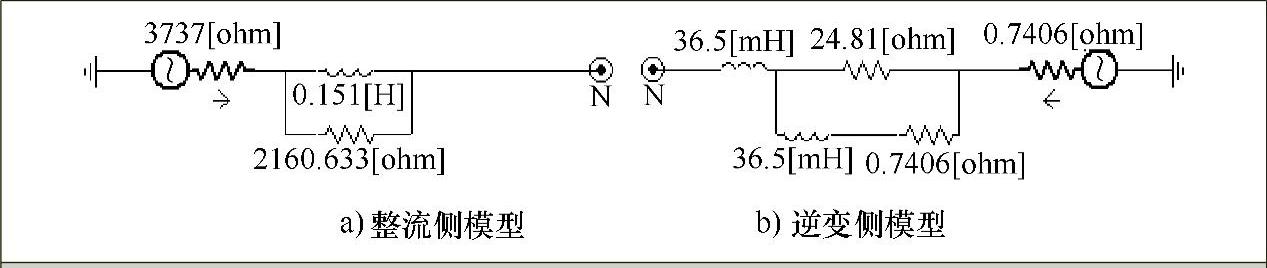
图7-18 交流系统等效模型
1.仿真参数计算及设置
（1）CIGRE HVDC标准模型参数设置
该系统为双桥12脉冲单极大地返回式直流输电系统。整流侧交流系统额定线电压为345kV，短路比SCR为2.5，额定直流电压为500kV，额定直流传输功率为1000MW，逆变侧交流系统额定线电压为230kV，SCR为2.5。为了省去公式中的比例系数，简化计算，仿真时引入了标幺值（per unit，p.u.）。标幺值是相对于某一基准值而言的，同一个数值，当基准值选取不同时，其标幺值也不同。标幺值的计算公式如式（7-1）所示。
标幺值=真实值/基准值 （7-1）
（2）主要参数基准值选取与标幺值
在选择基准值时必须和其实际值具有相同的量纲。例如，实际值为38.5kV的电压，当选取35kV为基准值时，其标幺值为1.1p.u.；当选取110kV为基准值时，其标幺值为0.35p.u.。图中所标注元件参数均为其真实值。主电路结构虽然简单，但两侧均为弱交流系统，运行条件较困难，然而用它作为研究的基础，可反映HVDC控制系统的主要问题。
系统的标幺基值见表7-1。
表7-1 系统标幺基值
整流侧无功补偿器和滤波器中的电容值与其对应的无功功率如表7-2所示。
表7-2 模型中整流侧的电容值及对应无功功率值
由于所有滤波器在工频频率下都呈现容性阻抗，因此滤波器装置除了抑制谐波以外，还可以兼做无功功率补偿器。滤波器所能供给的基频无功功率为滤波器容量，它与电容器供给的基频无功功率相等，滤波器能提供的无功功率可由式（7-2）求得。
Qc=U2ωC=U2·2πf·C=U2·314C （7-2）
系统中所有电容提供的无功功率之和为125+250+250=625（Mvar），正好是HVDC传输容量的一半以上。
逆变侧无功功率补偿器和滤波器中的电容值与其对应的无功功率如表7-3所示，换流变压器参数如表7-4所示。
表7-3 模型中逆变侧的电容值及对应无功功率值
表7-4 换流变压器参数
在第一个标准模型的参数设置下，经过仿真发现滤波器参数设置还有改进空间，可通过对交流侧滤波器的结构和参数进行重新优化和设置，从而进一步降低系统的交流侧谐波含量。
（3）交流侧滤波器的设置
改进后的标准结构模型交流侧滤波器的每个支路结构如图7-19所示，它应具有如下特性：较低次谐波和特征谐波应当被一个支路吸收；每个滤波器支路应当有相同的参数，且每个支路的额定功率为0.25p.u.（以额定直流功率为基值）。因此，两个相等的滤波器支路并联后，其额定功率即可达到0.5p.u.。
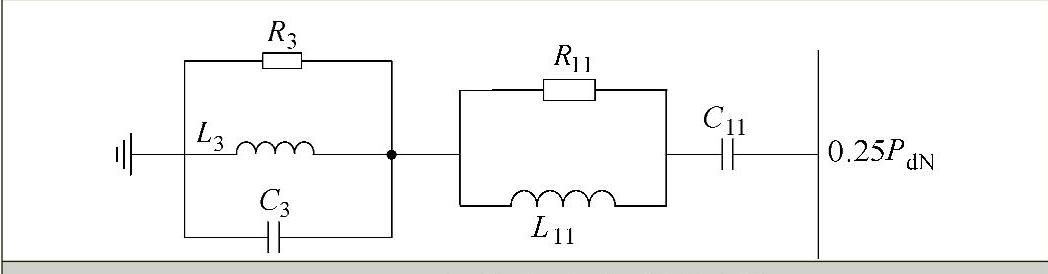
图7-19 新的交流滤波器结构
图7-19所示的交流滤波器参数见表7-5。
表7-5 交流滤波器参数
（4）输电线结构
第一个标准模型的输电线路采用的是电缆结构寄生的电容较大，与线路电感和平波电抗器连接后，将出现接近于基频的串联谐振。若再加上与交流侧二次谐波并联谐振的作用，则结果将使直流控制变得比较困难。因此，考虑用双远距离架空线的单级等值模型来代替原来的电缆结构模型，以改进原先的标准模型，为此，重新选择了与原来电缆结构具有相似谐振点的双极500kV直流线路结构的850mile单级等值模型作为新的输电线路模型。其参数如下：
r=0.04496Ω/mile，l=3.5989mH/mile，c=0.01610μF/mile
长度=850mile，Ls=597mH（整流侧），Ls=597mH（逆变侧）
（5）直流滤波器设置
改进的模型中采用双极远距离架空线必须要加入直流滤波器，直流滤波器结构如图7-20所示，其参数如表7-6所示。它由单调谐12次谐波支路和高通滤波器组成。
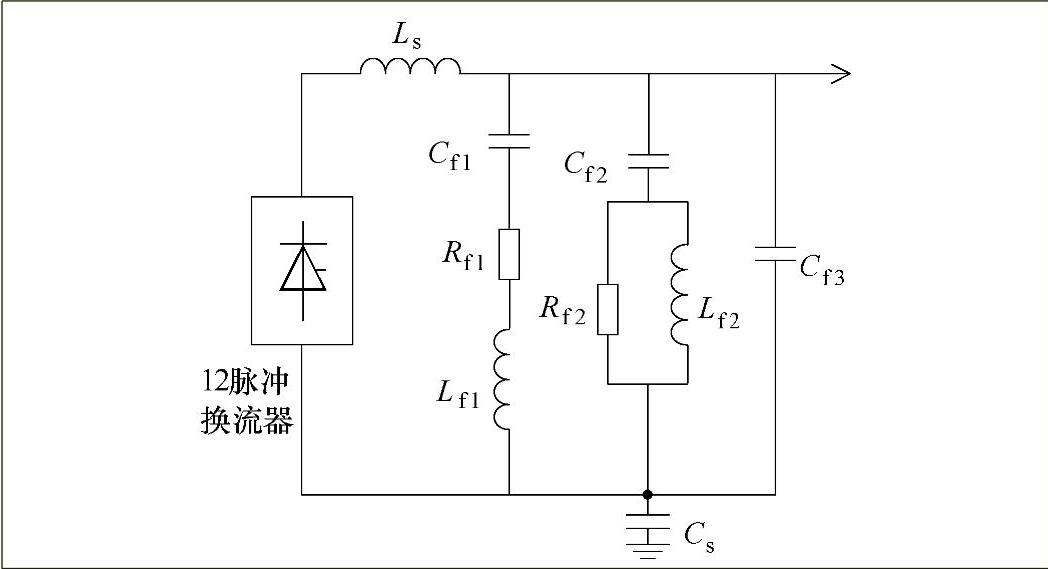
图7-20 直流滤波器结构
表7-6 整流侧无源滤波器参数(https://www.chuimin.cn)
（6）CIGRE HVDC改进型标准结构模型
CIGRE HVDC标准模型经过改进加入了改善后的交流滤波器和经过修正的远距离直流输电线路，如图7-21所示的改进型标准结构模型，其详细参数见表7-7。
表7-7 新标准结构模型下的主要参数
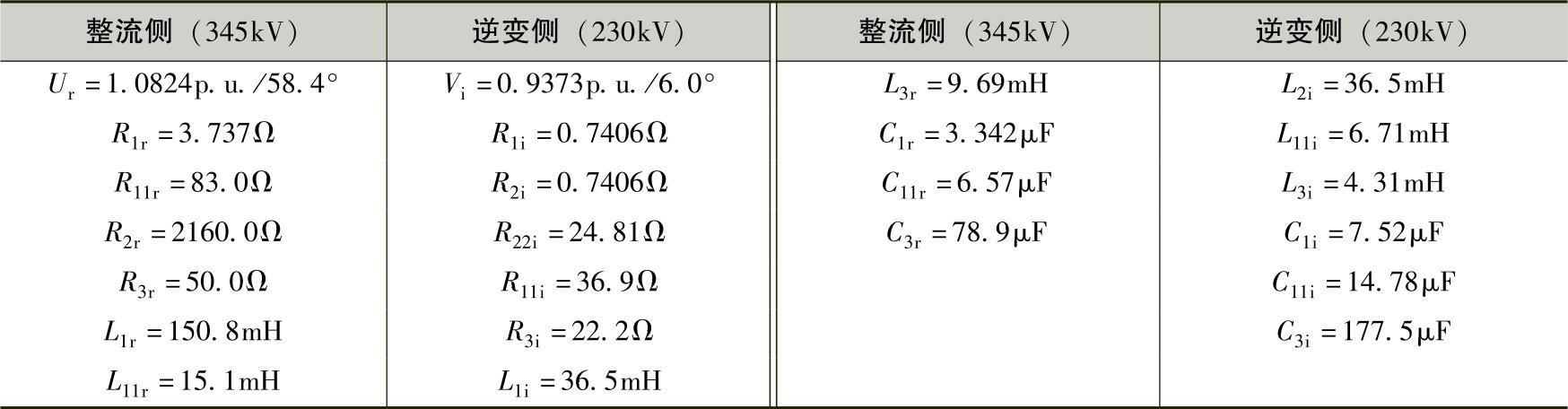
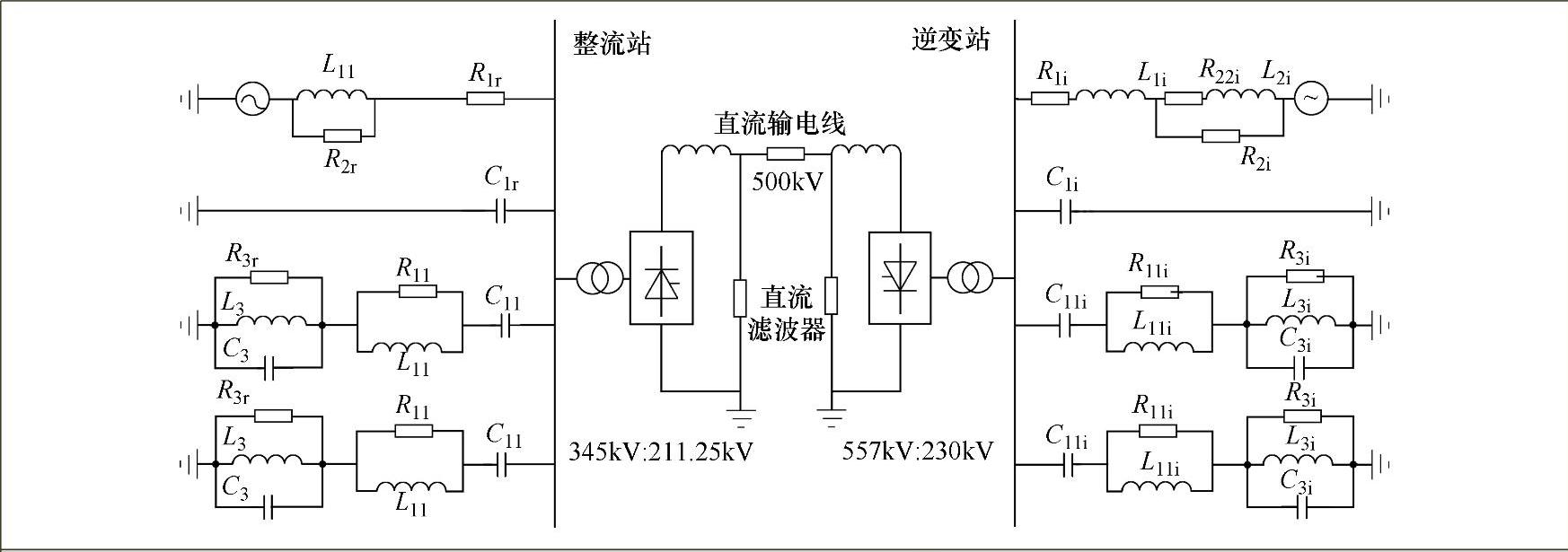
图7-21 修改的标准模型
2.仿真结果
对所建直流输电系统控制模型在正常稳态运行、直流侧接地故障、整流侧或交流侧三相短路故障以及系统交流侧谐波抑制分析等情况进行较详细的数字仿真，其结果如下。
（1）正常稳态运行
在正常稳态运行情况下，直流电压（DC Volts）、直流电流（DC Current）及传送功率（Power）均为额定值，则其对应的标幺值均为1p.u.。整流侧触发角αord（图中为Alpha）大约为20°，介于最大值和最小值之间。横轴为时间轴（单位时间为秒，下同），仿真时取的时间步长为50μs，纵轴为直流幅值的标幺值，其运行结果如图7-22所示。
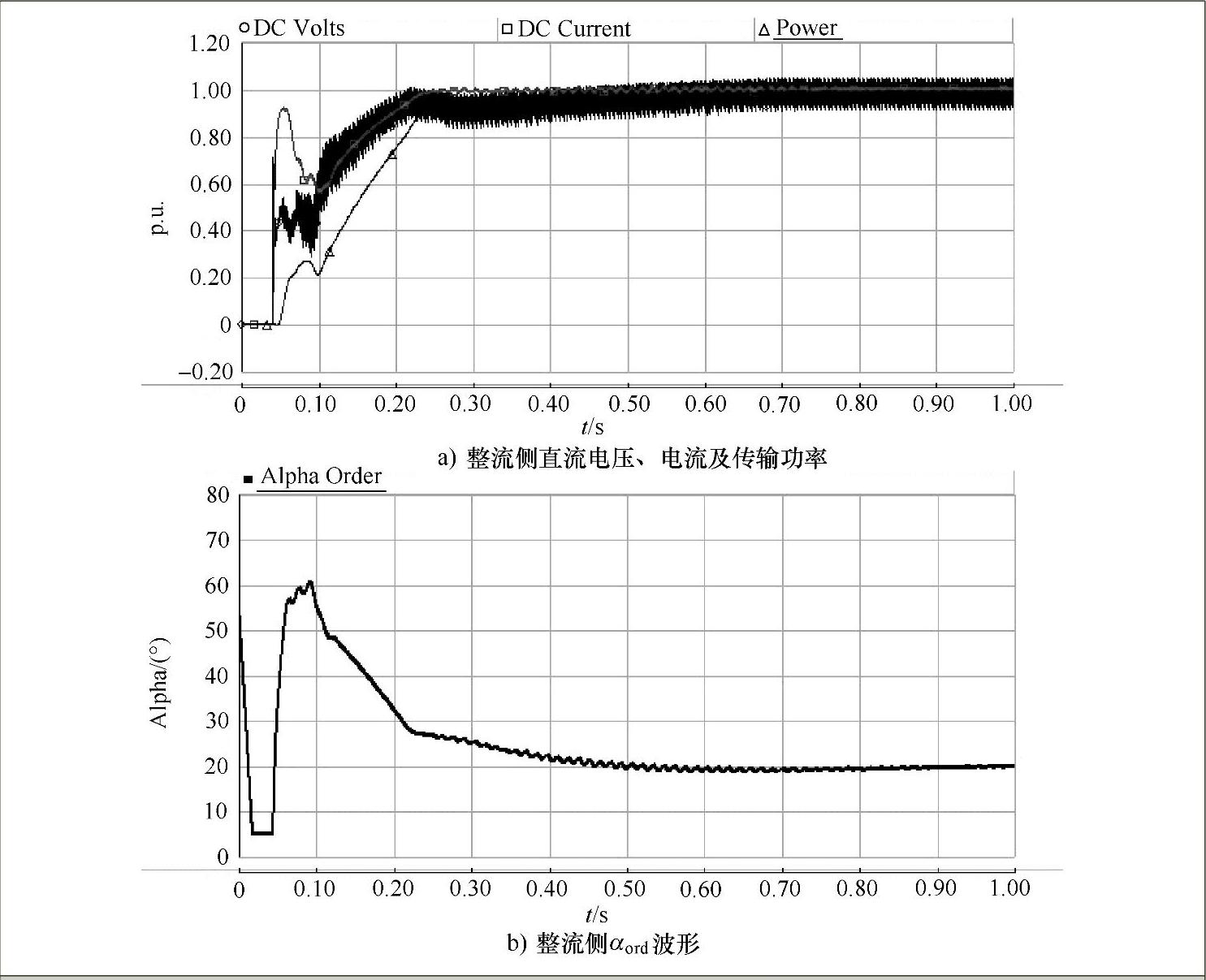
图7-22 正常稳态运行结果
从运行结果来看，在正常稳态运行下，该系统具有很好的跟踪性能，已经实现控制功能。
（2）直流侧接地故障
设在t=0.4s，直流线路发生接地故障，持续时间为0.3s，此时，DC Volts、DC Current、Power及整流侧触发角αord（图中为Alpha）的曲线如图7-23所示。
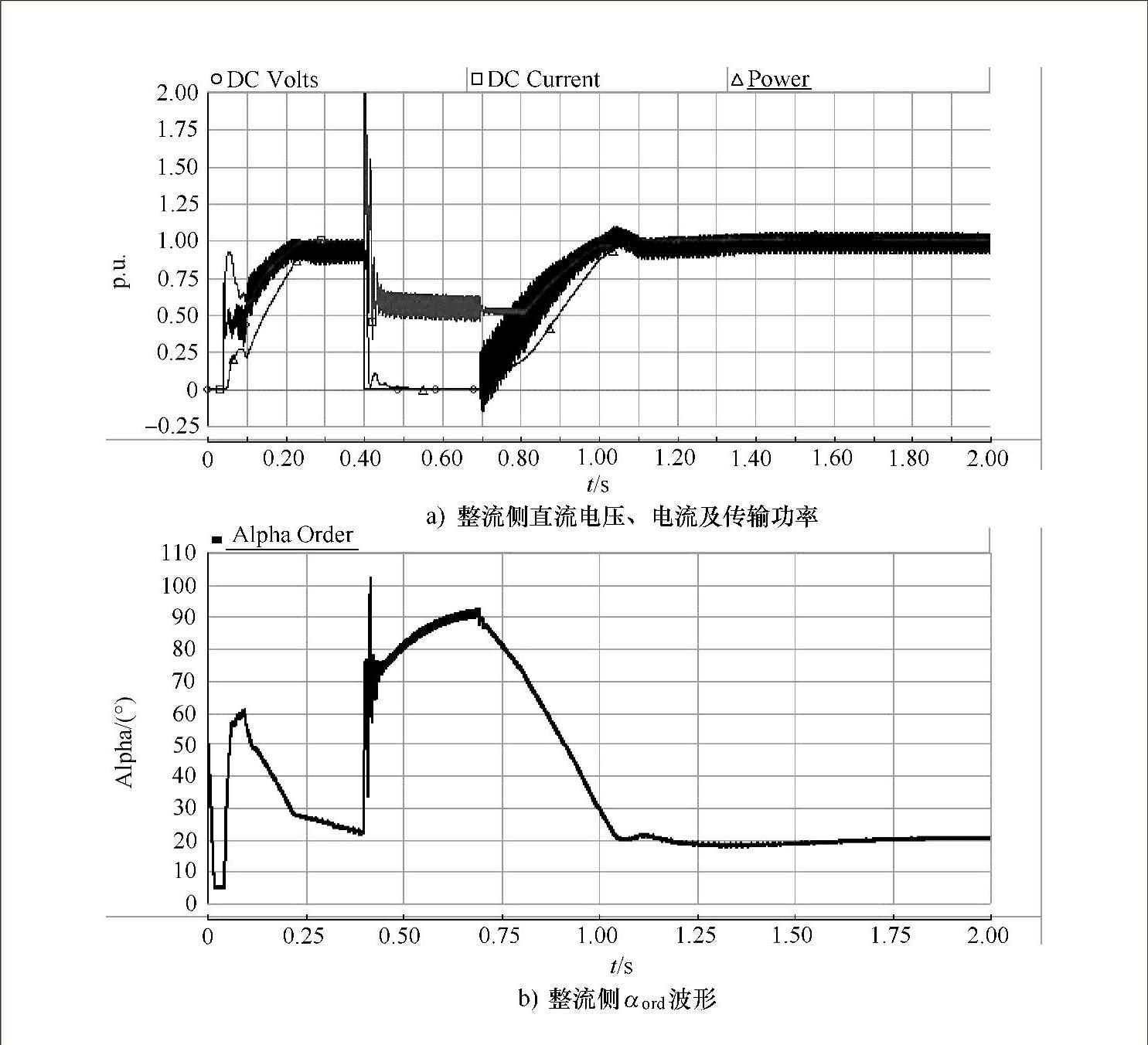
图7-23 直流侧接地故障运行结果
由仿真结果可得，在t=0.4s时，DC Volts立即跌落至0，DC Current则出现过大的电流。因控制系统中的低压限流单元VDCOL动作，DC Current参考值降低至0.55p.u.，同时αord快速升至约90°，从而使直流短路电路小于0.5p.u.。故障结束后，αord开始减少，DC Volts、DC Current逐渐上升，在t约为1s之后逐步恢复正常运行。
（3）整流侧或交流侧三相短路故障
使整流侧换流母线在t=0.4s发生三相直接接地短路故障，持续时间为0.2s，此时，DC Volts、DC Current、Power及整流侧触发角αord（图中为Alpha）的曲线如图7-24所示。
由仿真结果可以看出，在t=0.4s时，DC Volts立即跌落至0，DC Current则降低至0.5p.u.以下，由于整流侧恒电流控制动作，使αord减少，然后维持在最小触发角下运行，在故障期间整流侧的αord抑制在最小值，恢复过程中αord有波动，直流纹波较大。
（4）系统交流侧谐波仿真分析
下面将通过PSCAD仿真来分析滤波器的设置对第一个标准结构模型和改进型标准结构模型下交流侧的电流谐波所产生的影响。
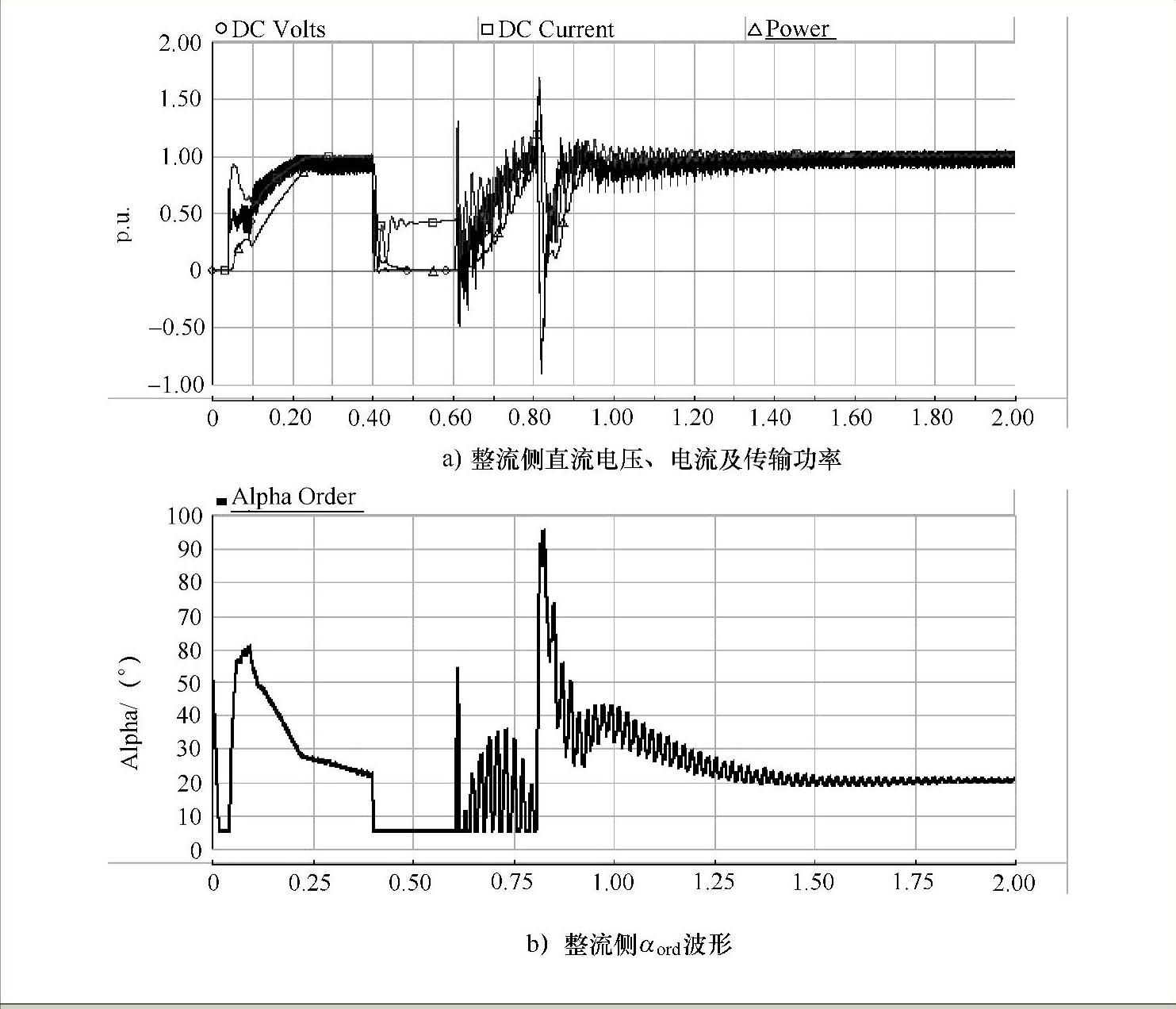
图7-24 整流侧短路故障运行结果
1）对于整个高压直流输电系统，当整流侧和逆变侧都没有滤波器和无功功率补偿装置时，整流侧交流系统的相电流波形如图7-25所示，横轴为时间轴，仿真时取的时间步长为50μs，纵轴为电流幅值的标幺值。相电流波形经过FFT变换后的谐波分布柱状图如图7-26所示。
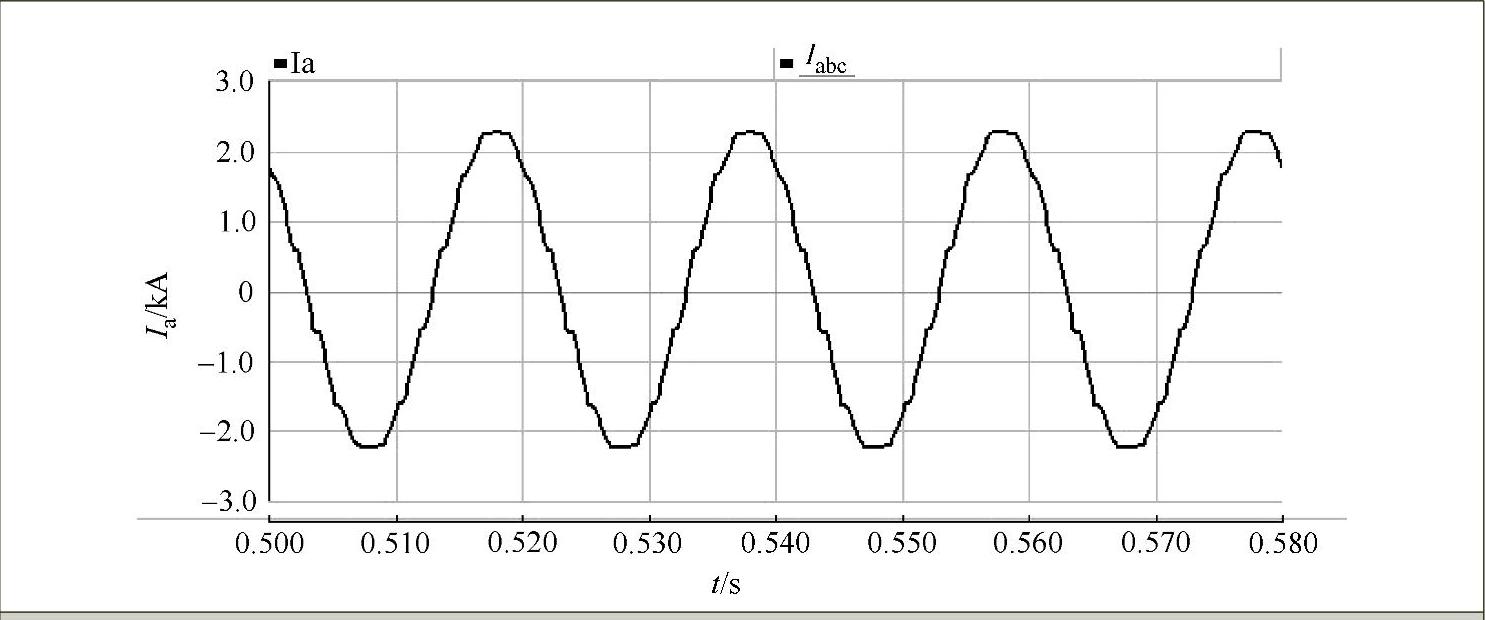
图7-25 无滤波器及无功补偿装置时整流侧交流系统相电电流
2）第一个标准模型的相电流仿真波形如图7-27所示，其经过FFT变换后的谐波分布柱状图如图7-28所示。
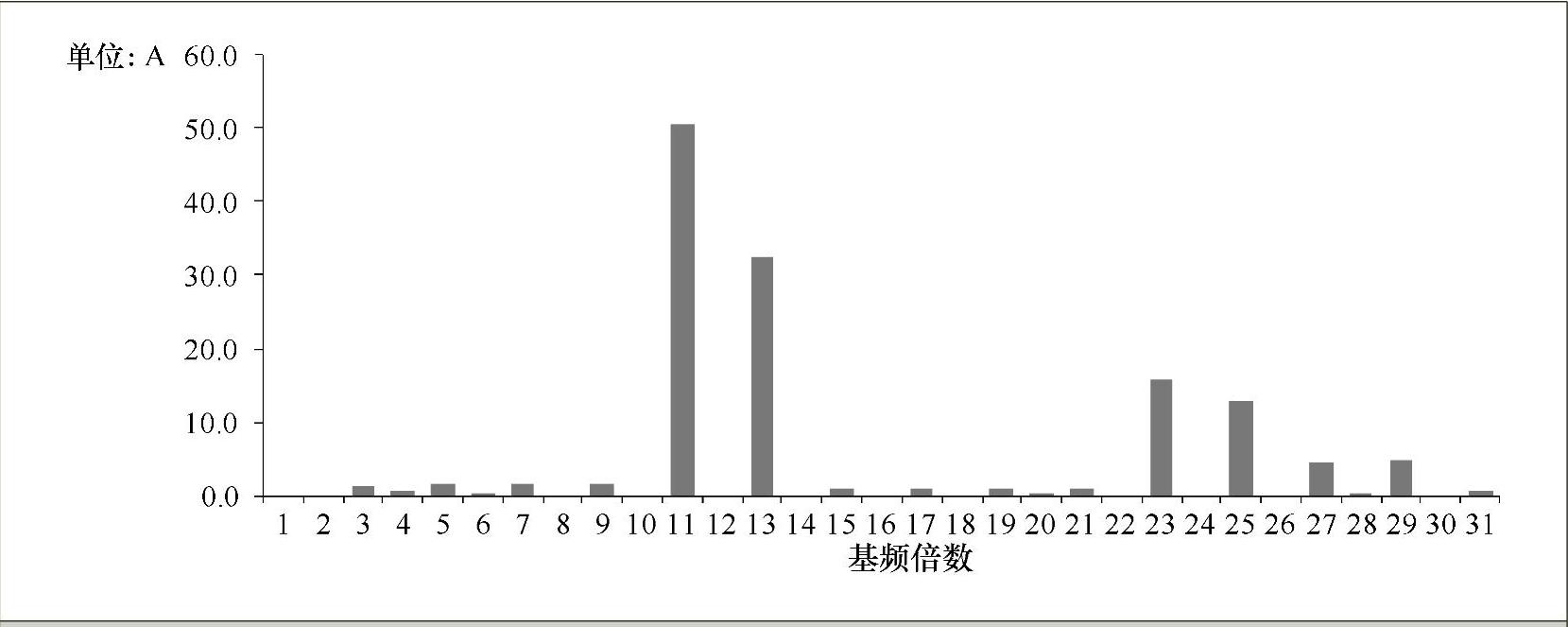
图7-26 相电流Ia经FFT变换后的柱状图
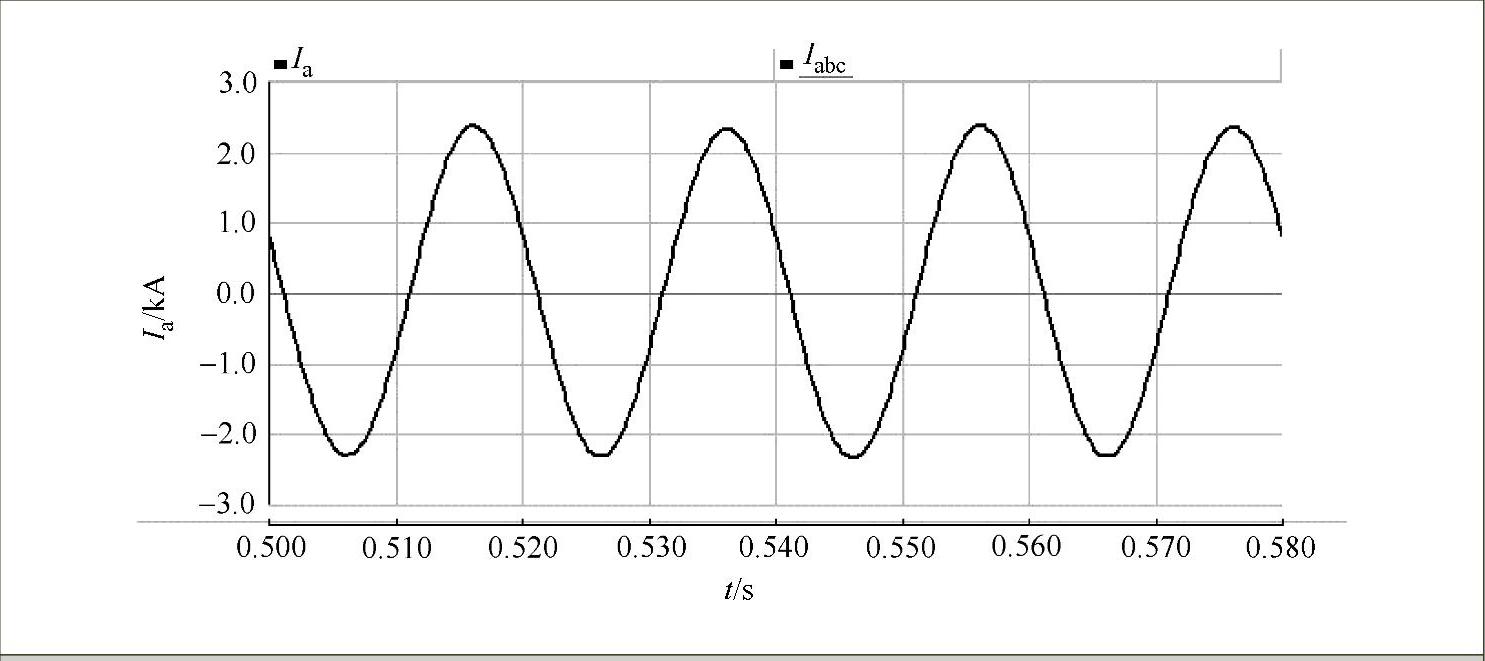
图7-27 第一个标准模型的相电流仿真波形
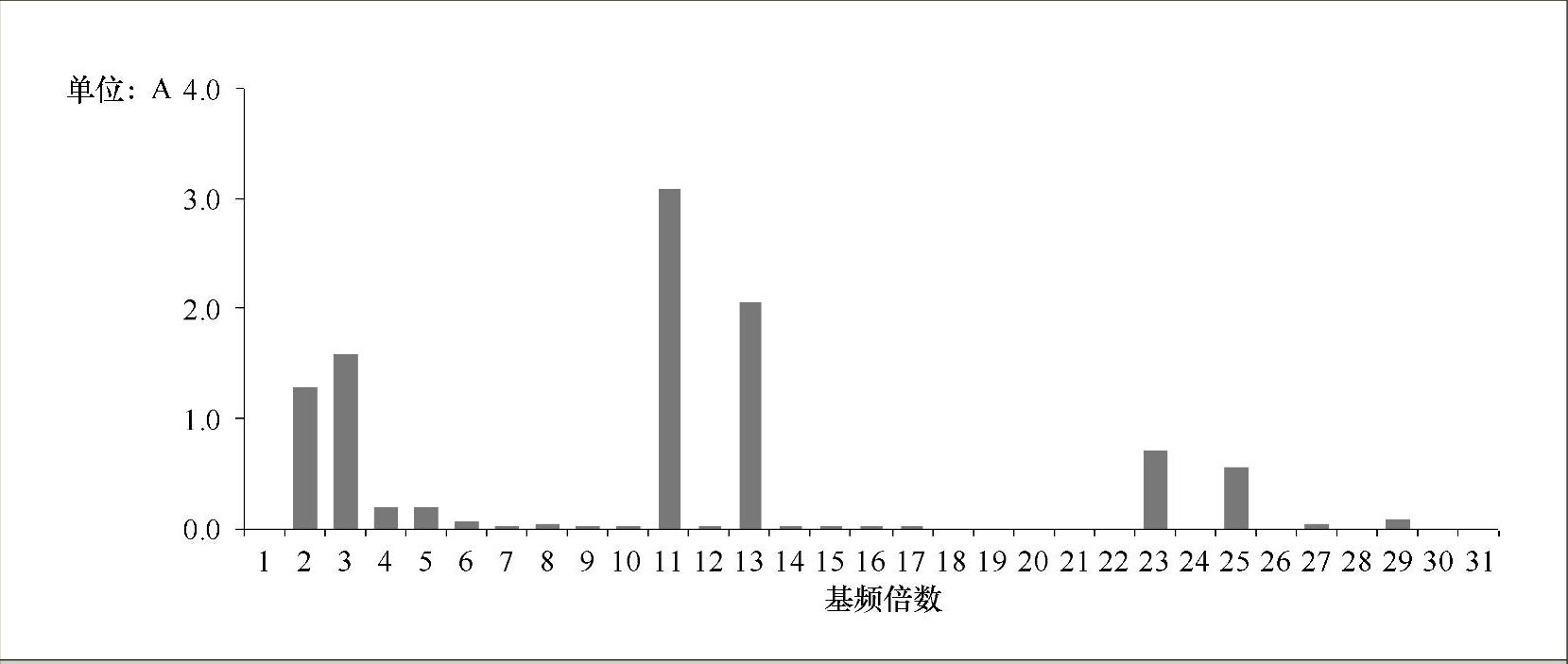
图7-28 相电流Ia经FFT变换后的柱状图
对比以上各图可以得出，电流总谐波畸变率比无滤波时的电流谐波总畸变率明显降低，表现最为显著的是：11次、13次、23次、25次谐波含量明显降低，但是3次谐波含量却略有增加，这是因为在交流侧加上无功补偿装置和无源滤波器组后，为3次谐波电流提供了流通通路而形成的。
3）在改进型标准结构模型中，对交流侧的滤波器进行了改进，仿真波形如图7-29所示。其经过FFT变换后的谐波分布柱状图如图7-30所示。
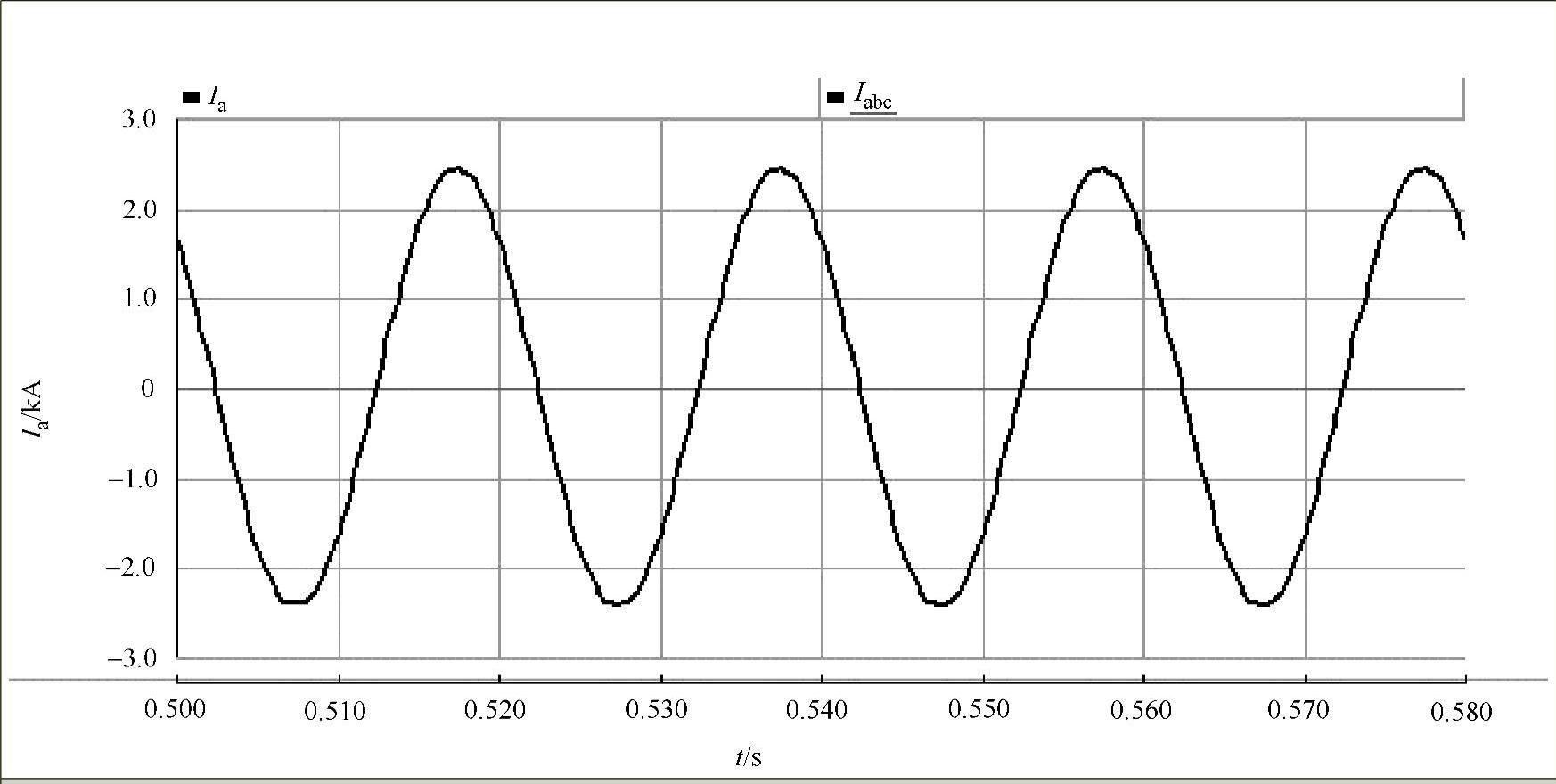
图7-29 改进型标准结构模型中的相电流仿真波形
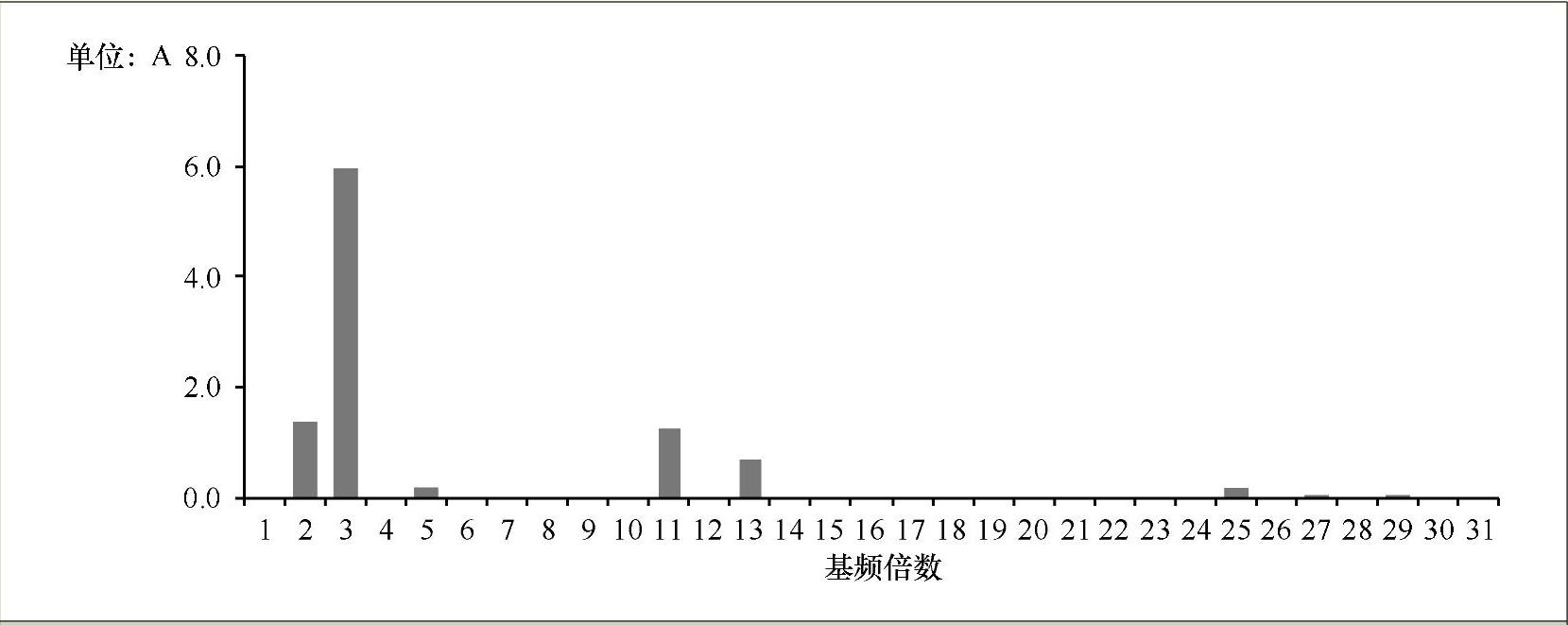
图7-30 修改后相电流Ia的谐波幅值柱状图
由仿真结果可以看出，在未采用滤波器时，电流畸变明显，在采用了无源滤波器以后，电流畸变下降了，从而验证了滤波器设计的合理性。对比图7-28和图7-30，可以看出图7-30中总的电流畸变率最小，因此可以看出改进型标准结构模型中的滤波器滤波效果最好，同时也验证了对标准模型修改的必要性。
正常情况下，直流电压（DC Volts）、直流电流（DC Current）及传送功率（Power）均为额定值，则其对应的标幺值均为1p.u。对改进型标准结构模型进行仿真可得到正常运行情况下的仿真波形如图7-31所示，对比图7-22a和图7-31可以看出，在标准模型的直流侧加入滤波器后，直流电压纹波明显比未加直流滤波器时少得多，而且在经过较短的调节时间后很快趋于平直，说明该系统具有良好的跟踪性能。
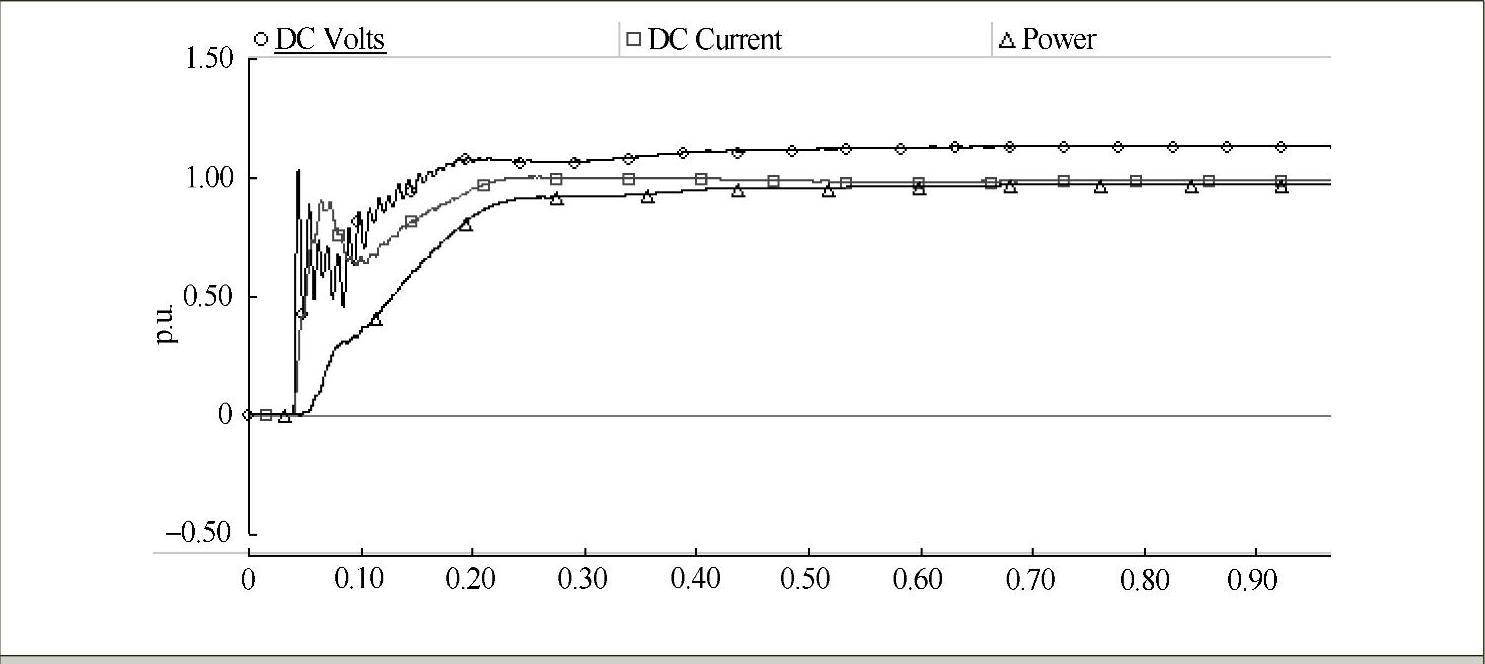
图7-31 修改模型的整流侧直流电压、电流及传输功率
相关文章
-
电容实体建模实例演示详细阅读
键，接着选择圆环体，按 键，此时实体模型效果如图9-67所示。...... -
MCB仿真分析：优化与探究详细阅读
在仿真中，采用动网格技术模拟动触头的运动过程，为了考虑栅片切割电弧后近极压降，模型中在栅片周围包含一层0.1mm厚度的鞘层，鞘层模型采用图8-22所示的非线性电阻。图8-64 MCB灭弧室内温度的分布a）0.05ms b）0.5ms c）3.5ms d）6.5ms图8-65 MCB电弧电压随时间变化的曲线......
2025-09-29
-
仿真模型的建立及分析结果详细阅读
图3-25 三角形隶属度函数模糊控制规则是模糊控制的核心，因此，如何建立模糊控制规则成为一个十分关键的问题。根据表3-3所示参数，由式可得D0=0.24；由式可得x0=[0.11573600]T；由式可得图3-28 模糊控制器输出曲线图3-28 模糊控制器输出曲线图3-29 有源电力滤波器整体仿真模型表3-3 仿真参数图3-29 有源电力滤波器整体仿真模型表3-3 仿真参数取正定矩阵取正定矩阵根据实验取定根据实验取定具体仿真结果如下：1）图3-30所示为无滤波器的情况下电网电流波形。......
2025-09-29
-
生成刀路轨迹及仿真优化方案详细阅读
Stage1.生成刀路轨迹Step1.进入区域切削模式。图3.5.10 “区域切削模式”对话框（一）注意：加工区域在“区域切削模式”对话框（一）中排列的顺序与选取切削区域时的顺序一致。此时“区域切削模式”对话框如图3.5.16所示，在下拉列表中选择选项，图形区中显示所有加工区域正投影方向下的刀路轨迹，如图3.5.17所示。图3.5.15 “往复切削参数”对话框图3.5.16 “区域切削模式”对话框（二）Step3.生成刀路轨迹。......
2025-09-29
-
Simulink简介及应用实例详细阅读
模型的创建与定义、模型的分析以及修正是使用Simulink的三大步骤，图10-3显示了典型的Simulink工作框图。图10-3 Simulink操作框图Simulink具有相对独立的功能和使用方法，它支持线性和非线性系统、连续和离散时间系统，而且系统可以多进程。进行Simulink仿真的主要步骤如下：1）运行Simulink：在MATLAB命令窗口中直接键入Simulink并回车就会显示图10-2的Simulink启动界面。......
2025-09-29
- 详细阅读
-
设计小结及常见问题分析优化详细阅读
过多使用文字标注，会明显影响原理图的设计区域，也妨碍图样的设计效果。事实上，设计无线高频的实用电路大多采用集成电路形式，因为集成电路可以最大限度地减少元件之间，导线之间的相互干扰；而全部采用独立元件的振荡电路在实际应用中较为少见。6）在自制元件的过程中，没有合理设置“Port”造成编译错误。由于原理图中元件的引脚线具有电气属性，“Port”的属性必须与之匹配。......
2025-09-29
-
开断特性仿真分析详细阅读
图8-3为额定电流为16A的微型断路器，当短路电流通过瞬动电磁铁线圈时，铁心向左移动，顶动脱扣杆，使机构脱扣。图8-3 微型断路器现对上述微型断路器描述其仿真过程。为了验证计算准确性，在预期电流Ip=10.2kA，U=232V，cosφ=0°，βv=4.5257×10-7条件下进行了开断试验，试验结果与计算机仿真进行了对比，如图8-7所示。......
2025-09-29
相关推荐