在风力发电系统中，风力机风能捕获的过程直接决定了风力发电系统的风能利用效率。在风速恒定的情况下，风轮产生的机械功率可表示为......
2023-06-23
风力机数学模型的优化方案
【摘要】：在风力发电系统中，风力机风能捕获的过程直接决定了风力发电系统的风能利用效率。三叶片风力机叶尖速率比的典型值为8～10。定桨距风力机的优点是控制较为简单，其缺点是叶片结构复杂、笨重、整体效率较低。变桨距风力机是另外一种风力机，其与定桨距风力机的不同之处在于其可通过改变桨叶节距角来充分利用风能。图5-34 风力机的风能利用系数C特性曲线
在风力发电系统中，风力机风能捕获的过程直接决定了风力发电系统的风能利用效率。在风速恒定的情况下，风轮产生的机械功率可表示为
式中，Pwt为风轮捕获的风能；ρ为空气密度；R为风轮扫过的面积；v为风速；Cp（λ，β）为风能利用系数，是风轮机叶尖速率比λ和桨距角β的非线性函数。
风能利用系数通常可用下式来计算[136]
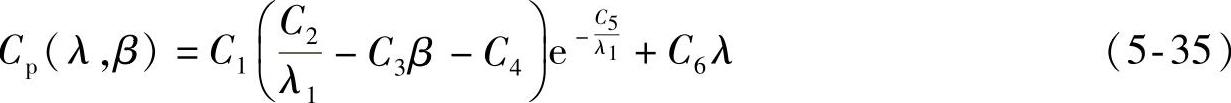
式中
式中，C1=0.5176，C2=116，C3=0.4，C4=5，C5=21，C6=0.0068。
叶尖速率比λ为风轮叶尖线速度和风速的比值，即
λ=Ω lR/v （5-37）
式中，Ω l为风轮的转速。
三叶片风力机叶尖速率比的典型值为8～10。叶尖速率比影响风力发电机的风能利用系数，如图5-34所示。
风力机主要分为定桨距和变桨距两种。定桨距风力机的特点是桨叶与轮毂的连接是固定的，当风速变化时，桨叶的迎风角度不能随之改变，只能利用桨叶翼型本身的失速特性，在风速高于额定风速时，降低效率，自动将功率限制在额定值附近。桨叶的这一特性，通常称为自动失速性能。因而，对于这类风力机而言，当风速改变时，不能通过调整桨叶的节距来改变气流对叶片的攻角，从而改变风力机组获得的空气动力转矩而保持输出功率稳定，而只能依靠改变发电机转速来调节风电机组功率，因而定桨距风力发电机组属于变速恒频风力发电系统。定桨距风力机的优点是控制较为简单，其缺点是叶片结构复杂、笨重、整体效率较低。变桨距风力机是另外一种风力机，其与定桨距风力机的不同之处在于其可通过改变桨叶节距角来充分利用风能。在一定风速范围内，通过桨距（气流对叶片的攻角）控制而维持风机转速的稳定，而在风速过大时，除了对桨叶进行节距控制外，还通过控制发电机转子电流来控制发电机转差率，使发电机转速在一定范围内能够快速适应风速的变化，从而使输出功率更加平稳。由于变桨距风力发电系统中，风力机转速在一定风速范围内可维持恒定，并能得到恒频的电能，因而可构成恒速恒频风力发电系统。
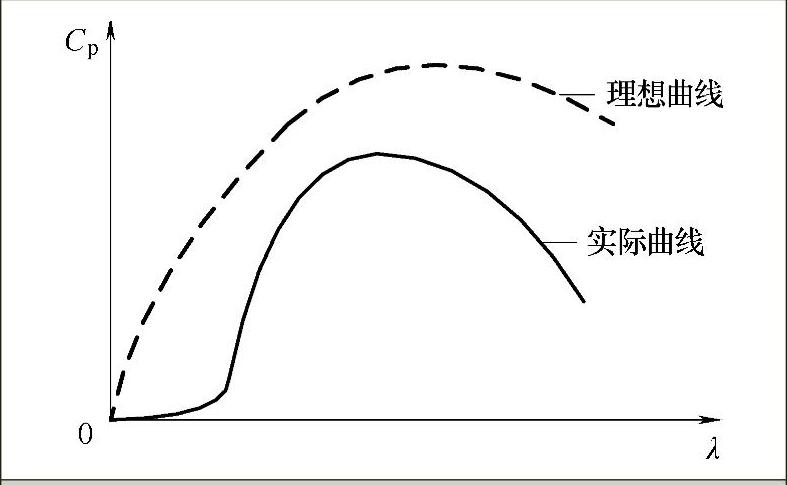
图5-34 风力机的风能利用系数C特性曲线
有关电力电子技术在电力系统中的应用的文章
- 详细阅读
-
无人机数学模型与实物的关联优化方案详细阅读
图6.12 数学模型并不等于实物，而这正是数学模型的重要优势之一。我们都有通过直接的观察或亲手的操作来取得对无人机感触与理解的经验。在本节开头已经说过，数学模型可以帮助我们定量分析无人机内部的结构、性质。我们可以用数学公式来建立无人机每个部分、每个方面的数学描述。......
2023-07-05
-
长江中游江湖联算耦合数学模型优化方案详细阅读
表7.3-1长江干流2003—2006年不同河段冲淤量实测值与验证值对比注 表中负值表示河道冲刷。洞庭湖区采用2003年四口河系地形资料和2006年长江干流和洞庭湖湖盆地形资料，对模型进行验证计算。......
2023-06-21
-
数学模型基本框架优化详细阅读
5.2.1.2模型参数计算方法在式、式中， 为河道的泥沙综合恢复饱和系数，它与河道断面形态，冲淤状态及水流泥沙运动参数有关，βs为反映断面流速和输沙不均匀分布的系数。......
2023-06-22
-
数学模型计算结果优化详细阅读
图13-24异重流潜入位置变化过程表13-7水库运用初期1～5年库区输沙计算结果图13-24异重流潜入位置变化过程表13-7水库运用初期1～5年库区输沙计算结果在相同的水沙条件及边界条件下进行的小浪底库区实体模型试验结果表明，距坝67km 以下库段总淤积量为29.44 亿m3，若淤积物干容重γ0=1.15t/m3，则淤积量为33.8亿t。......
2023-06-23
-
全沙数学模型的建立与优化详细阅读
10.4.2.4沉降系数确定图10-16航道疏浚深度与悬沙沉降系数的关系在悬沙不平衡输沙方程和河床变形方程式中，沉降系数α 对河床冲淤强度有较大影响。......
2023-06-22
-
风力发电数学模型优化详细阅读
式中 vs——风力发电机的启动风速,m/s；vc——风力发电机的截止风速,m/s；vi——第i时刻的风速,i=1,2,…,n,且vs≤vi,vi+1≤vc；Pi——风速功率曲线对应风速为vi时风力发电机输出的功率,kW。......
2023-06-23
- 详细阅读
相关推荐