双桥换流器运行分析

2025-09-29 理论教育版权反馈

【摘要】：双桥12脉冲整流器工作在正常运行工况下时，触发延迟角α和换相重叠角γ需满足0＜α＜90°-γ/2，且γ＜30°。为了简要分析双桥换流器的工作原理，此处仅就VT11、VT12、VT21、VT22四个桥臂同时导通过渡到VT12、VT21、VT22、VT31四个桥臂同时导通的过程进行原理分析。

在大容量高压直流输电系统中，通常采用双绕组换流变压器型式的12脉冲变流器作为换流站的主要拓扑，如图4-6所示。12脉冲换流器由两个6脉冲换流器在直流侧串联而成，其交流侧通过换流变压器实现并联。换流变压器的阀侧绕组一个为星形联结，另一个为三角形联结，从而使两个6脉冲换流器的交流侧能得到相位相差30°的换相电压。

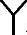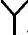下面将简要分析图4-6所示的12脉冲换流器的工作原理。在分析之前，先假设/接线换流变压器超前于/△接线换流变压器。在此基础上，桥1对应阀臂的开通时间将先于桥2的对应阀臂30°导通，而每个单桥的6个晶闸管依然按照60°的间隔顺序轮流导通。因此，晶闸管的导通顺序为VT₁₁、VT₁₂、VT₂₁、VT₂₂、VT₃₁、VT₃₂、VT₄₁、VT₄₂、VT₅₁、VT₅₂、VT₆₁、VT₆₂、VT11（循环）。每个相邻桥臂的导通时间间隔为30°。其中，桥臂编号的第1个数字表示其在本单桥内的导通顺序，第2个数字代表其所在单桥的编号。例如，阀臂VT₁₂指桥2中的第1个阀臂。

双桥12脉冲整流器工作在正常运行工况下时，触发延迟角α和换相重叠角γ需满足0＜α＜90°-γ/2，且γ＜30°。为了简要分析双桥换流器的工作原理，此处仅就VT₁₁、VT₁₂、VT₂₁、VT₂₂四个桥臂同时导通过渡到VT₁₂、VT₂₁、VT₂₂、VT₃₁四个桥臂同时导通的过程进行原理分析。

1.VT₁₁、VT₁₂、VT₂₁、VT₂₂导通阶段

此时，两个单桥中的上、下半桥中各有一个阀臂导通，直流电流i_d通过这四个阀臂、直流输电线路以及交流系统构成闭合回路。当假设换流变压器电压比为如下数值时，交流三相电流可分别用式（4-14）～式（4-17）来表示。

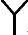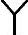/型换流变压器T₁电压比k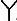/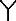=1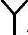；/△换流变压器T₂电压比k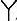/Δ=3/1。

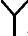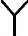/型换流变压器的网侧和阀侧电流为

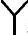/△换流变压器的阀侧电流为

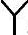/△换流变压器网侧电流为

交流系统电流为

因为直流电流i_d没有纹波，所以换流变压器的网侧和阀侧绕组以及交流系统中的电流恒定不变，这些电流不会在换流变压器的两侧绕组以及交流系统等值电抗中产生电压降，因此两个单桥的整流电压分别为u_d1=u_ac和u_d2=u_c。双桥12脉冲整流器的整流电压为

u_d=u_d1+u_d2=u_ac+u_c

2.阀臂VT₃₁开始导通

此时，VT₃₁阳极和阴极之间的电位差为u_VT31=e_ba。此时，阀臂VT₁₁、VT₁₂、VT₂₁、VT₂₂、VT₃₁同时导通。

3.阀臂VT₁₁、VT₁₂、VT₂₁、VT₂₂、VT₃1同时导通

此时，12脉冲整流桥1的上半桥中阀臂VT₁₁和VT₃₁通过换流变压器T₁及交流系统的a、b两相构成闭合回路，使交流系统两相短路。假设沿此闭合回路流动短路电流i_k，其流通方向如图4-14所示。

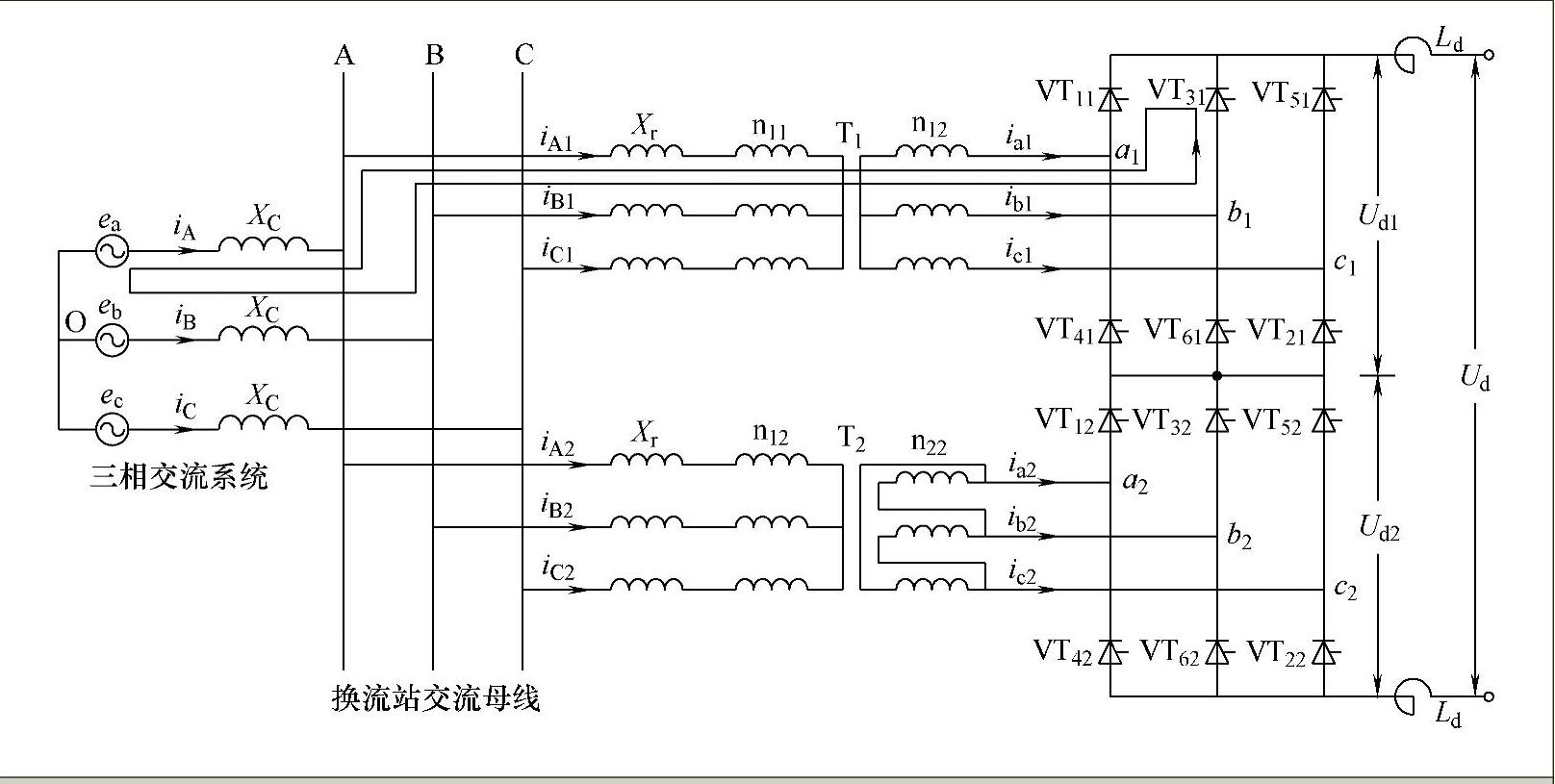
图4-14 双桥12脉冲整流器换相示意图

则/型环流变压器网侧和阀侧电流可表示为

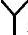/△型换流变压器的阀侧和网侧电流不变，同式（4-15）和式（4-16）所示。则由基尔霍夫定律，可给出交流系统的三相电流表达式为

与单桥整流器换相工作相类似，针对图4-14所示的两相短路闭合回路列写电压平衡方程式，并将上述各支路表达式代入电压方程，就可得到

(https://www.chuimin.cn)

若考虑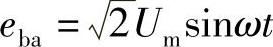和初始条件i_k（α）=0，则短路电流i_k可表示为

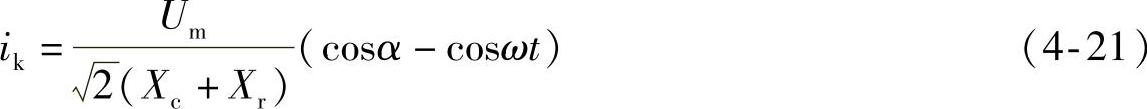
式中，U_m为交流系统电源线电压有效值；L_C、L_r分别为交流系统和换流变压器的每相等值电感。

短路电流的幅值为

从式（4-21）中可以看出，换相导致交流系统两相短路时，单桥和双桥换流器的短路电流表达式相似，不同之处在于换流器的交流侧各相电路的等值电感。因此，双桥整流器短路电流的变化以及换相阀臂中电流的变化形式与单桥整流器相同，同时也说明在双桥换流器中本桥的换相不受邻桥的影响。

双桥整流器中每个单桥的换相角γ计算式与6脉冲整流器相同，即

式中，γ为换相重叠角。

桥1换相期间，整流输出电压表达式为

u_d1=（u_ac+u_bc）/2 （4-24）

此时，桥2的整流输出电压仍然保持u_d2=u_c。桥1的换相并没有影响桥2的整流电压。

4.VT₁₂、VT₂₁、VT₂₂、VT₃₁导通阶段

VT₁₁向VT₃₁换相结束时，阀臂VT₁₁上流过的电流为零，使VT₁₁关断，只有VT₁₂、VT₂₁、VT₂₂和VT₃₁继续导通。桥1的整流电压u_d1=u_bc，桥2的整流电压仍为u_d2=u_c，则双桥整流器的整流电压变为u_d=u_d1+u_d2=u_bc+u_c。上述分析表明双桥换流器中每个单桥的整流电压波形与6脉冲换流器的整流电压波形相同。

由于换流变压器T₁和T₂连接组别差异而导致两个单桥的换相电压产生30°的角度差，桥1和桥2的整流电压波形也会出现30°的角度之差，于是双桥12脉冲整流器的整流电压u_d=u_d1+u_d2波形为两个单桥整流电压波形叠加的结果，如图4-15所示。

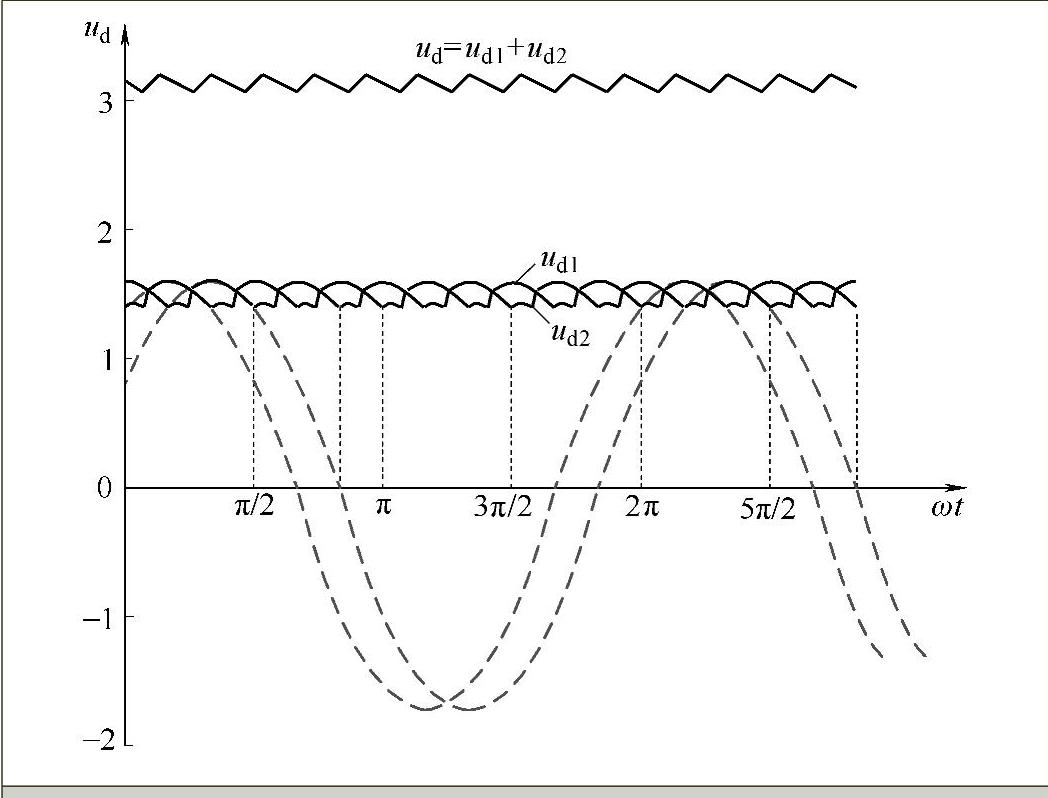
图4-15 双桥换流器整流电压叠加示意图

5.桥间的相互影响

虽然双桥整流器在正常运行工况下，一桥的换相与否不会影响另一桥的电流和电压，但两个单桥既然有物理上的联系，就必然存在相互影响，这种影响主要表现为一桥的换相使另一个桥的所有未开通阀臂上的阳极与阴极电位之差，即阳极电压发生畸变。这种畸变可能使下一个待开通阀臂在触发信号发出时，由于电压为负而不能开通，即出现开通延时。

在此，以VT₁₁、VT₁₂、VT₂₁、VT₂₂、VT31同时导通为例来说明双桥之间的相互影响。下一个待开通阀臂应该是VT₃₂。从图4-6中可见，其阳极电压为

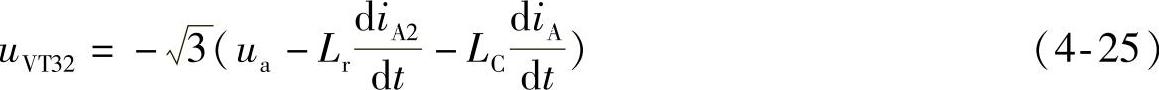
将式（4-16）和式（4-19）代入上式，并计及式（4-20），则上式变成

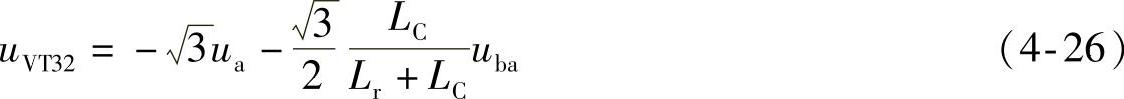
上式第二项体现了桥1换相对桥2的影响。令

系数K为桥1和桥2之间的相互影响系数，它反映了两桥之间相互影响的程度。系数K的变化范围为0～1。当K趋近于1时，表明桥1换流器和桥2换流器之间的相互影响越强，换相导致邻桥未开通阀臂的电压畸变就越严重；反之，若K趋近于0，则表明桥1和桥2之间的相互影响越弱，换相致使邻桥未开通阀臂的电压畸变就越轻微。交流系统越强，则由式（4-26）可知，系数K的占比就越小，桥1和桥2之间的相互影响就越弱。如果换流器与无限大交流系统相连，则两桥之间就几乎不存在相互影响。由此说明，双桥12脉冲换流器两桥之间相互影响的实质是两桥共有一个耦合电感，即交流系统每相等值电感L_C。

双桥换流器运行分析

相关推荐