首页理论教育模型参考自适应控制优化方案

模型参考自适应控制优化方案

2023-06-23 理论教育版权反馈

【摘要】：图3-24所示为设计的模型参考自适应控制方案。那么图3-24 模型参考自适应控制方案可得自然频率wn=30rad/s，调节时间ts≈3.15T1≈0.25s，同时得到参考模型的两个极点-12.6061和-71.3939。为达到控制目标，自适应控制器输出由系统模型定义为Dδ=KT·xδ+θT·r 式中，K=[K1，K2]T和θ分别为闭环系统的反馈增益和前馈增益。上式代入单相并联型APF动态模型式，得定义跟踪误差e=xδ-xm 这里的控制目标为找到一个自适应控制律使跟踪误差e趋近于0。

图3-24所示为设计的模型参考自适应控制方案。关于参考模型，由于其动态性能表征了实际系统对动态性能和响应特性的理想要求与期望，在这里，设计其为一个过阻尼二阶系统，选取阻尼比ζ=1.4，上升时间

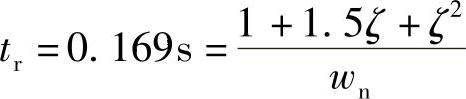
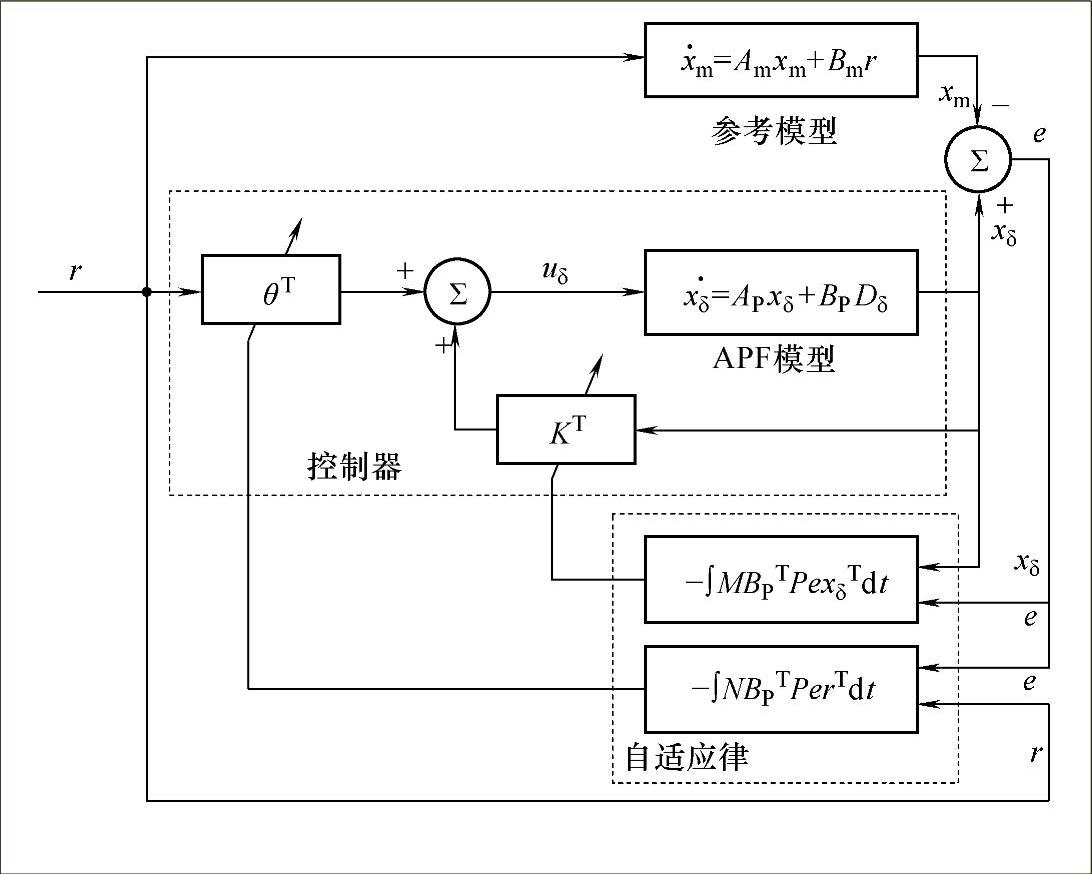
图3-24 模型参考自适应控制方案

可得自然频率w_n=30rad/s，调节时间t_s≈3.15T₁≈0.25s，同时得到参考模型的两个极点-12.6061和-71.3939。那么

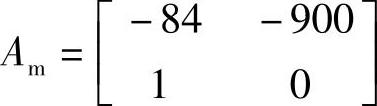
在不断实验后确定B_m=［500040］^T时，系统效果较好。具体的参考模型状态空间模型为

建立的单相并联型有源滤波器的动态模型为

定义跟踪误差

e=x_δ-x_m （3-16）

这里的控制目标为找到一个自适应控制律使跟踪误差e趋近于0。为达到控制目标，自适应控制器输出由系统模型定义为

D_δ=K^T·x_δ+θ^T·r （3-17）

式中，K（t）=[K₁（t），K₂（t）]^T和θ（t）分别为闭环系统的反馈增益和前馈增益。上式代入单相并联型APF动态模型式（3-15），得

如果反馈增益K（t）和前馈增益θ（t）收敛，最优参数K^∗和θ^∗将由自适应控制器调整以便被控模型与参考模型相匹配，满足

对跟踪误差求导并将上式代入

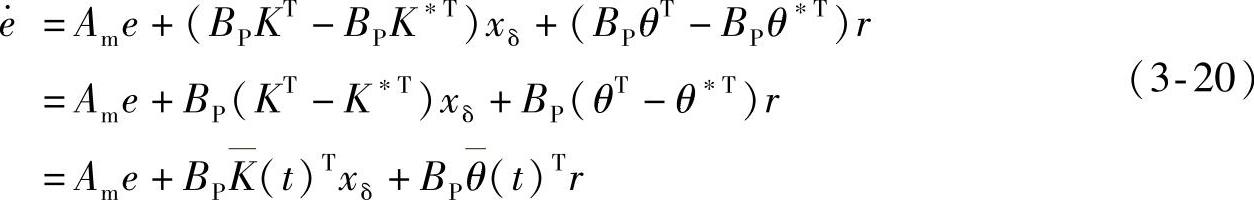
式中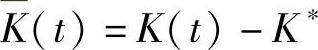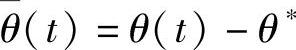，、为参数误差。

考虑如下的Lyapunov函数

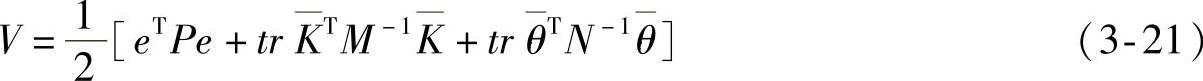
式中，P、M、N为对称正定矩阵；tr为迹（trace）的数学符号。

由于A_m是Hurwitz（霍尔维兹）稳定矩阵，存在唯一的2×2正定对称矩阵P满足

式中，Q=Q^T为2×2正定矩阵。

V（t）沿式（3-20）的迹的导数为

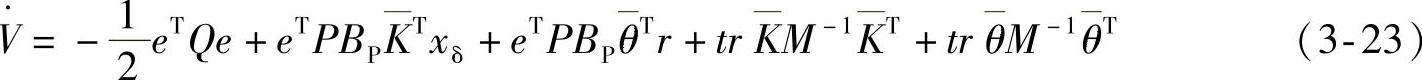
上式右边第2、第3项为标量，由矩阵迹的性质x^TAx=tr（xx^TA）、tr（A）=tr（A^T），上式可写成

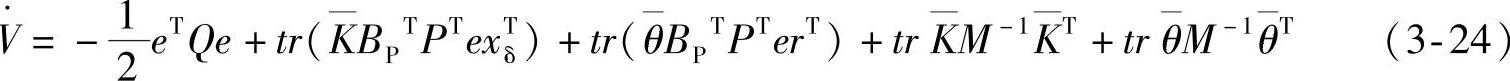
因此，令

将式（3-25）代入式（3-23）可得

上式说明始终是负值，即在任何初始条件下e是有界的。因为，所以V（t）是单调非递增并且有界的。

即有

根据Barbalat定理，当t→∞时e→0，因此，可以推导出系统是渐进稳定的。

则由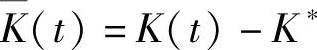、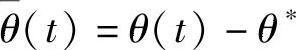，得到如下的参数自适应律：

自适应控制输出为

D_δ（t）=K^T（t）X_δ（t）+θ^T（t）r（t）（3-30）