首页理论教育有源电力滤波器的动力学模型

有源电力滤波器的动力学模型

2023-06-23 理论教育版权反馈

【摘要】：本节主要研究的是单相并联电压型有源电力滤波器，基本电路结构图如图3-22所示。由图3-23可以看出，建立单相并联型有源滤波器的动态模型，当Us＞0时，由APF工作的两个模式又可以得到图3-23 两种开关状态下的APF模型等效电路图当Us＜0时与此类似。为了减少控制器的设计难度，考虑上述非线性状态方程。上式即为近似线性化后的APF状态空间方程。占空比D0可表示为式中，x02、x01分别为Uc、iL的等效值。

本节主要研究的是单相并联电压型有源电力滤波器，基本电路结构图如图3-22所示。

图3-22所示的APF的工作过程可分解为两个模式。设其中四个开关管的开关转换频率为f_s，转换周期为T_s=1/f_s，占空比D=T_on/T_s。

图3-22 并联型APF的基本电路结构

模式1：当0≤t≤DT_S时，V₂、V₃导通，V₁、V₄关断，在这种模式，电感电流i_L正向增加，电磁能存储在电感L中。同时，储存在电容C中的能量分别转换到L和续流负载R中，电容放电。

模式2：当DT_s＜t≤T_S时，转换过程与模式1相反，此时储存在电感L中的能量转化到C、R和线路中，电容C充电。

由图3-23可以看出，建立单相并联型有源滤波器的动态模型，当U_s＞0时，由APF工作的两个模式又可以得到

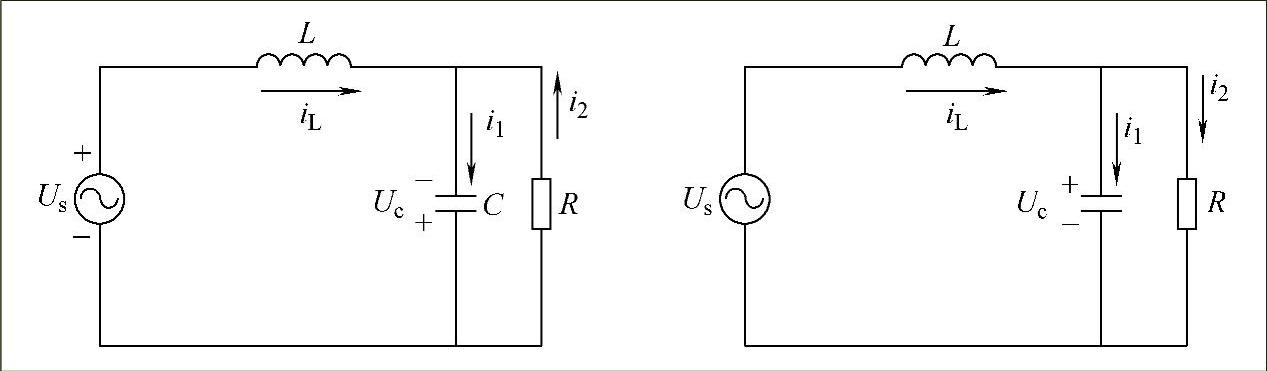
图3-23 两种开关状态下的APF模型等效电路图

当U_s＜0时与此类似。式（3-4）、式（3-5）所表述的是动力方程，为方便理解、分析，将其转换为关于电流、电压的平均状态方程，因而引入、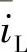分别表示U_c、i_L在一个周期内的状态变量的平均值，即

式中，τ是积分函数的时间变量，且τ∈[t，t+T_s]。

因此，由式（3-4）、式（3-5）观察可得逆变器的平均状态矢量方程为

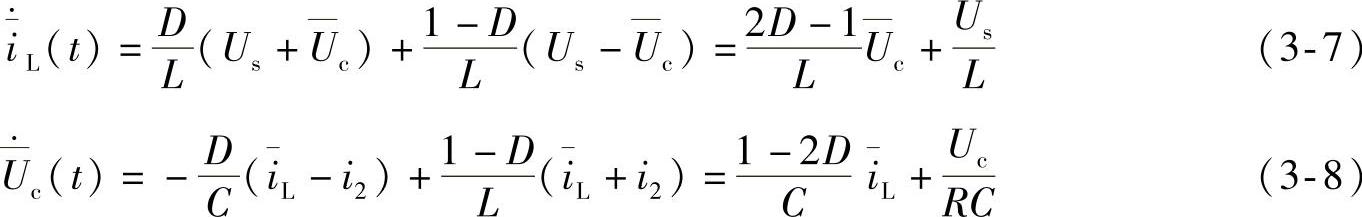
式中，D∈[0，1]。

另外，将式（3-7）、式（3-8）表述成如下形式：

式中，，，，。

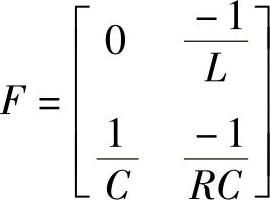为了减少控制器的设计难度，考虑上述非线性状态方程。如果x=x₀、D=D₀满足

f（x₀，D₀）=Fx₀+Gx₀D₀+EU_s=0

则（x₀，D₀）为平衡点。

令f（x₀，D₀，U_s，t）=Fx₀+Gx₀D₀+EU_s=0，在（x₀，D₀）处对式（3-9）的右边进行泰勒级数展开，忽略一次以上的高次项，得

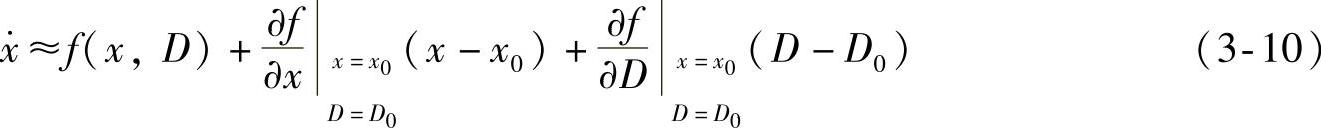
设x_δ=x-x₀、D_δ=D-D₀，在（x₀，D₀）附近可近似得到

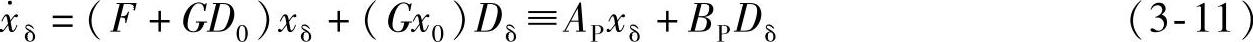
式中，A_P=F+GD₀、B_P=Gx₀。上式即为近似线性化后的APF状态空间方程。在非线性状态方程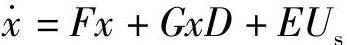的平衡点（x₀，D₀）处，电容电压和电感电流分别为

式中，x₀₂、x₀₁分别为U_c、i_L的等效值。占空比D₀可表示为