电流谐波含量过高的开关电源在电网某一路上密集安装使用时，会使三相四线制供电系统的中线电流急剧增加，大大超出相电流，引起中线超负荷，造成中性点电压偏移，很容易导致开关电源大批损坏。这是未采取有效谐波滤波技术的原因，有的还会引起火灾，造成重大经济损失。因此，无论是从保证电力系统的安全、经济运行来看，还是从保护用电设备和人身安全来看，必须严格控制并限定电流谐波含量，以减小谐波污染造成的严重危害。......
2023-06-25
谐波电流检测技术详解
【摘要】：指令电流运算电路的核心是谐波电流实时检测方法，实时、精确地检测出电网中瞬时变化的谐波电流，是提高APF补偿精度的一个关键问题。下面介绍几种常见的谐波电流检测技术，并将重点介绍应用最广泛的基于瞬时无功功率理论的谐波检测技术。
指令电流运算电路的核心是谐波电流实时检测方法，实时、精确地检测出电网中瞬时变化的谐波电流，是提高APF补偿精度的一个关键问题。下面介绍几种常见的谐波电流检测技术，并将重点介绍应用最广泛的基于瞬时无功功率理论的谐波检测技术。
1.基波电流减去法
这是最早应用于指令电流运算的一类方法，采用模拟滤波器将基波电流分量滤除，得到谐波分量；或采用带通滤波器得出基波分量，再与被检测电流相减得到谐波分量。这种方法存在许多缺点，如设计难、误差大、对电网频率和电路元件参数十分敏感等，因而极少采用。
2.频率分析法
该方法是从傅里叶级数中导出的，根据采集到的一个电源周期的电压、电流值进行计算，最终得到所需的谐波和无功电流。其缺点是由于傅里叶变换需要进行大量的运算，因此计算复杂，延时较长，实时性较差，难以实现瞬时检测。
3.瞬时空间矢量法
利用瞬时无功功率理论，首先检测出电压与负载电流，然后分别计算出瞬时有功功率和瞬时无功功率，滤去基波分量后得到谐波瞬时有功功率和瞬时无功功率，即得出所需补偿电流指令值。这种方法能快速跟踪补偿电流，进行及时补偿，但计算较为复杂且检测精度相对不高。
4.基于现代控制理论的方法
最早应用的现代控制理论方法有基于PI控制器的方法，但由于其控制特性不能适应电网和负载的变化，后来又提出了基于模糊控制和滑模控制等方法。它们都是直接根据有源滤波器逆变器直流侧的电压和电流值，求出被补偿的电网电流的基波有功分量，进而求出补偿所需的谐波电流的值。
5.自适应检测法
从自适应滤波算法中的自适应干扰对消原理衍生出的自适应检测法，检测过程为先求出基波有功分量，然后从待检测电流中排除掉基波有功分量，即可得到补偿电流的指令值。该方法突出的优点是对电网畸变电压、电网频率及参数变化有较好的自适应能力，但其动态响应较慢，需要一定的周期才能稳定[5，93-95]。
6.神经网络检测法
神经网络检测法是随着神经控制理论的应用发展而形成的一种新型智能手段。人工神经网络自学功能强，以进化算法和方向传播用于神经网络的拓展训练，但是算法较为复杂，检测速度有一定的局限。
7.基于瞬时无功功率理论的谐波检测技术
在各国学者提出的众多检测方法中，得到广泛应用的是20世纪80年代初H.Akagi提出的基于瞬时无功功率理论的谐波检测技术。目前，瞬时无功功率理论已经成功地应用到三相三线制系统并取得了良好的补偿效果，而且其应用从原先的三相三线制系统逐步扩展到其他类型的电路，如单相电路、三相四线制电路以及直流输电等更为广泛的领域。
瞬时无功功率理论[4-5]的实质是将n次谐波变换为n-1次谐波信号，故一般的5、7、11、13、17等奇次谐波将变为200Hz、300Hz等的交流信号，而基频分量变为直流信号。根据数字信号处理理论，将直流信号从包含200Hz甚至更高频率的信号中分离出来，低通滤波器的参数要经过综合考虑，才能满足很高的滤波精度和足够快的响应速度。实际中，滤波精度和响应速度两者是相互矛盾的。
三相电路瞬时无功功率理论的基本理论如下：假设三相电路中的电压和电流瞬时值分别为ea，eb，ec和ia，ib，ic，采用C32变换矩阵，将它们变换到αβ两相正交坐标上有
式中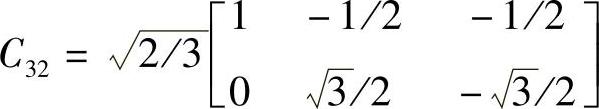
αβ坐标系中的电压和电流矢量如图3-5所示。图示αβ平面中，矢量eα、eβ和iα、iβ可分别合成（旋转）电压矢量e和电流矢量i。φe、φi分别为e、i的幅角。瞬时无功和有功在αβ坐标系下可表示为
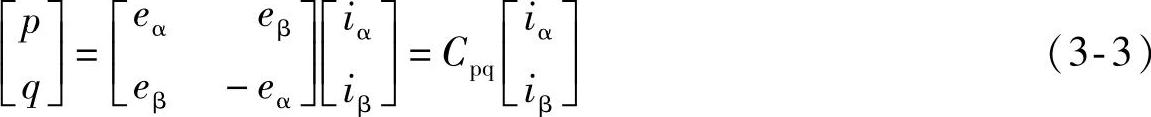
式中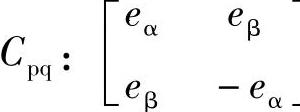
。
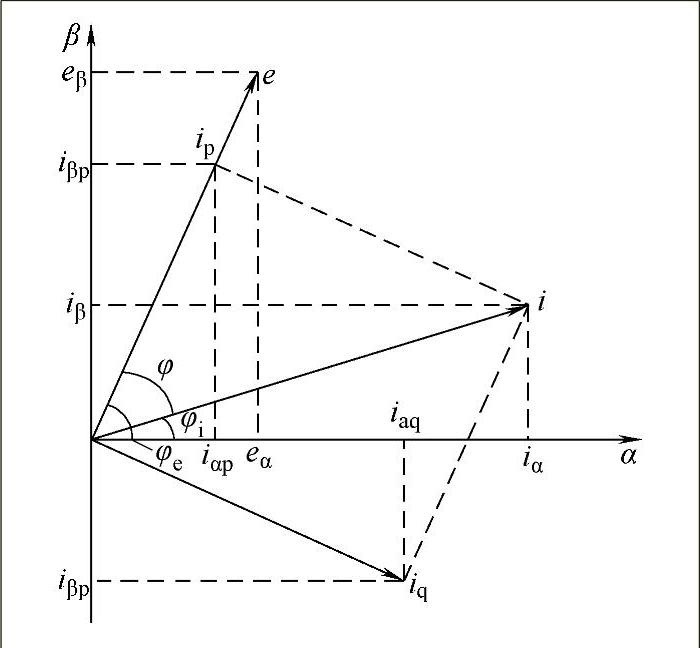
图3-5 αβ坐标系中的电压和电流矢量
瞬时无功功率理论在正弦对称电压和对称负载条件下，所定义的各物理量有其明确的物理意义。由于该技术是针对有源电力滤波器开发出来的，因此它仅需或仅能得到三相电路的总谐波电流含量，这对于电力系统中许多尚需检测出电网中任意次谐波电流的应用场合有一定局限性。同时，在电压非正弦和负载不对称条件下，该理论中的各定义量不再有明确的物理意义。
p-q法是基于三相电路瞬时无功功率的一种谐波检测方法，此种方法不受电网电压畸变的影响，可以迅速准确地检测出负载电流的谐波分量，具有实时性好、准确度高等优点。原理如图3-6所示。
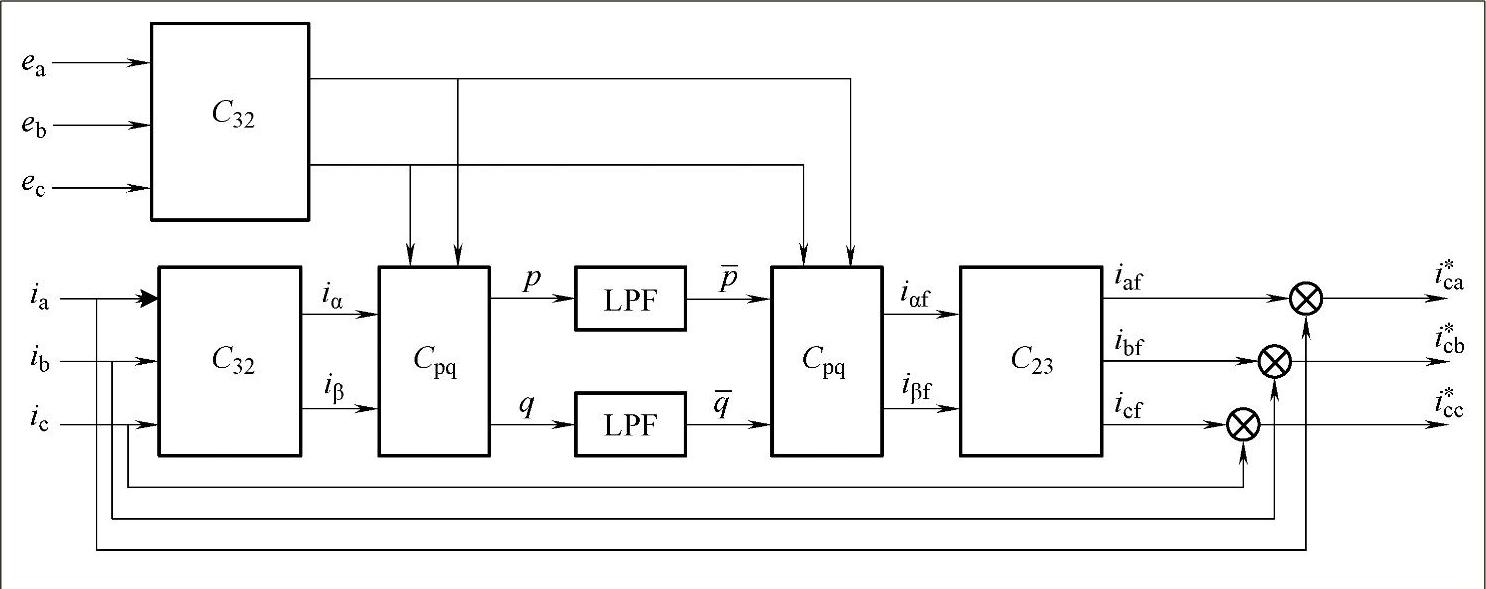
图3-6 p-q运算方式原理图
有关电力电子技术在电力系统中的应用的文章
- 详细阅读
-
直流耐压和泄漏电流试验详解详细阅读
对电力电缆进行直流耐压及泄漏电流试验是检查电力电缆绝缘状况的一个主要试验项目。直流耐压试验与泄漏电流试验是同时进行的。与交流耐压试验比较，直流耐压及泄漏电流试验的优点是：1）对电缆线路进行耐压试验，所需试验设备容量小。就是说，直流耐压试验更容易发现绝缘缺陷。7）直流耐压试验时，应在试验电压升至规定值后1min以及加压时间达到规定时，测量泄漏电流。......
2023-06-27
-
电流电压信号检测方法优化详细阅读
霍尔传感器是比较理想的快速电流、电压信号检测传感器，它的核心器件是霍尔器件。将被检测的电压信号与LEM霍尔电压传感器的一次线圈及检测电阻RI相连接，构成回路，将检测的电压转换为霍尔电压传感器一次线圈的电流，该电流......
2023-06-30
-
肌醇的检测方法详解详细阅读
肌醇广泛分布在动物和植物体内，是动物、微生物的生长因子，对降低胆固醇、促进健康毛发的生长、防止脱发有帮助。肌醇不含双键，没有特征性的紫外吸收，也没有与反相柱的相互作用力，所以不能用反相色谱与紫外检测器来测试。本方法是用离子色谱和电化学电极来测试肌醇。准确移取1 mL肌醇原始标准溶液至100 mL容量瓶中，加水定容，摇匀后即可注射。......
2023-07-02
-
短时耐受电流试验详解详细阅读
三相或单相动、热稳定联合试验时，应在额定短路持续时间内的一次试验中同时获得规定的动稳定电流和热稳定电流有效值，其I2t值和动稳定电流峰值IMC不得低于规定值，且与规定值之差，I2t不得超出10%，IMC不得超出5%。动稳定电流峰值为试验电流波形图第一周波内的电流最大峰值，如图2-1中IMC。......
2023-07-02
-
如何降低交流整流电路中的电流谐波？详细阅读
图4-1 交流整流电路与输入电压、电流波形脉冲电流中含有大量的谐波，这些不同频率的每一个正弦波成分都被称为谐波分量。如果以基波100%为基础，则通常经桥式整流电容滤波的输入电流中，3次谐波分量达到77%以上，5次谐波达到50%，7次谐波达到40%，总的谐波电流含量会高出基波值，往往会达到117%左右，输入功率因数只有0.65。......
2023-06-25
-
单向晶闸管检测方法详解详细阅读
图解演示单向晶闸管是由P-N-P-N4层3个pn结组成的。在检测单向晶闸管时，通常需要先辨认晶闸管各引脚的极性，图4-56所示为待测单向晶闸管的实物外形。图解演示将万用表的黑表笔搭在晶闸管的控制极引脚上，红表笔搭在阳极引脚上，检测晶闸管控制极与阳极之间的正向阻值。5）若R5、R6值不为无穷大，则说明单向晶闸管有故障存在。......
2023-06-26
-
接触器检测方法详解详细阅读
下面我们就以交流接触器为例介绍接触器的检测方法，图4-42所示为交流接触器的检测方法。因此，对该交流接触器进行检测时，需依次对其内部线圈电阻值及内部开关在开起与闭合状态时的电阻值进行检测。由于是断电检测交流接触器的好坏，因此，需要按动交流接触器上端的开关触头按键，强制将触头闭合进行检测。⑤若测得接触器内部的四组开关有任何一组损坏，说明该接触器损坏。......
2023-06-22
相关推荐