深入解析2.5p-q功率基础理论

2025-09-29 理论教育版权反馈

【摘要】：而三相瞬时有功功率具有清晰且被普遍接受的物理意义，同时在暂态过程中也是适用的。图2-12给出了用两个瓦特表测量三相三线制三相负载平均功率的测量接线图。p-q理论是在三相系统中定义的，这里所指的三相系统可以有中性线也可以无中性线。

正如前面分析所知：Clarke正变换和反变换具有功率不变的特性。因此，Clarke变换非常适合用于分析三相系统中的瞬时功率。传统功率的定义有个前提条件，即系统必须处于稳态。而三相瞬时有功功率具有清晰且被普遍接受的物理意义，同时在暂态过程中也是适用的。

三相瞬时有功功率P_3ph（t）可以通过相电压和线电流的瞬时值来计算，即

P_3ph（t）=u_a（t）i_a（t）+u_b（t）i_b（t）+u_c（t）i_c（t）（2-103）

也就是

P_3ph=u_ai_a+u_bi_b+u_ci_c （2-104）

式中，u_a、u_b和u_c为相电压瞬时值；i_a、i_b和i_c为线电流瞬时值。

在没有中性线的系统中，u_a、u_b和u_c是以一个公共的参考点来测量的，有时这个参考点可以为“大地”，也可以为任意选择的公共参考点。例如，若将c相作为公共参考点，则测量到的“相电压”和三相瞬时有功功率P_3ph（t）就变为

P_3ph=（u_a-u_c）i_a+（u_b-u_c）i_b+（u_c-u_c）i_c=u_aci_a+u_bci_b （2-105）

由式（2-105）就不难明白为什么在n线系统中可以利用（n-1）个瓦特表来测量有功功率。图2-12给出了用两个瓦特表测量三相三线制三相负载平均功率的测量接线图。(https://www.chuimin.cn)

如果利用坐标变换将abc坐标系中的量替换为αβ静止坐标系中的分量，则三相瞬时有功功率就可以用αβ分量来计算，即

P_3ph=u_ai_a+u_bi_b+u_ci_c=u_αi_α+u_βi_β+u₀i₀ （2-106）

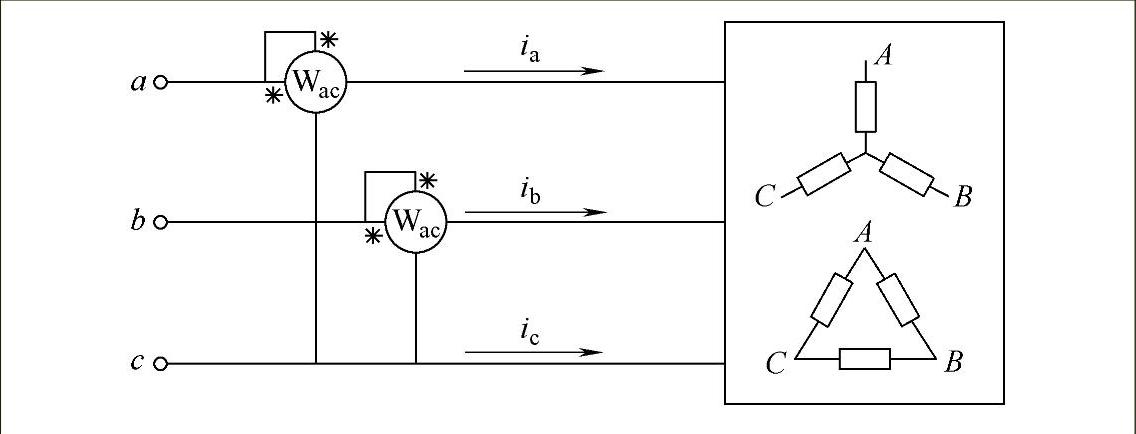
图2-12 二表法测量三相三线制三相负载平均功率的测量接线图

Clarke变换的功率不变特性在式（2-106）中得到了证明，p-q理论也利用了这个特性。

p-q理论是在三相系统中定义的，这里所指的三相系统可以有中性线也可以无中性线。此时，瞬时功率分为如下三个分量：瞬时零序功率p₀、瞬时实功率p和瞬时虚功率q。上述瞬时功率的定义是基于αβ坐标系下的瞬时相电压和瞬时线电流来定义的，即

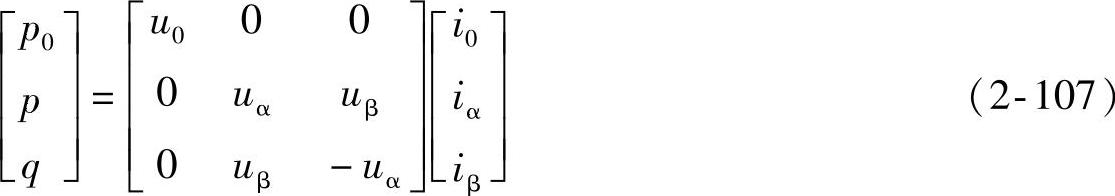
在三相三线制系统中，无零序电流，i₀=0。此时，只存在α、β轴上的瞬时功率。由于u₀i₀总等于零，因而在三相三线制系统中，代表单位时间内总能量流的实功率p可以由α、β分量来表示，即P_3ph=p。而瞬时虚功率q，由于其物理意义并非传统上的概念，则将在后面进行详细解释。