电剔压除和零电序流分矢量量的测量方法

2025-09-29 理论教育版权反馈

【摘要】：上述电压和电流仅仅由单个基波正序分量构成。如果将abc三相的瞬时电压和瞬时电流直接在复平面上组成电压和电流矢量，也会得到同样的结果。三相瞬时电压和瞬时电流的矢量已在电力电子领域中得到了广泛应用，特别是交流传动矢量控制、功率变换器的空间矢量脉宽调制以及有源滤波器等电力调节器的控制等。

如果u₀可以被忽略，根据电压的α轴瞬时分量和β轴瞬时分量就可以定义一个瞬时电压矢量，即

u=u_α+ju_β （2-92）

类似地，如果i₀可以被忽略，则可以定义一个瞬时电流矢量为

i=i_α+ji_β （2-93）

上述的瞬时矢量可以在复平面上表示。其中，实轴为α轴，虚轴为β轴。这些矢量也是时间的函数，它们是由三相系统中的瞬时相电压和瞬时线电流的Clarke分量构成。因而，此处不能将这些矢量简单地误认为相量。利用这种矢量还可用来定义一种新的概念——瞬时复视在功率。

考察一个三相线性电路中三相对称正弦相电压，有如下表达式成立：

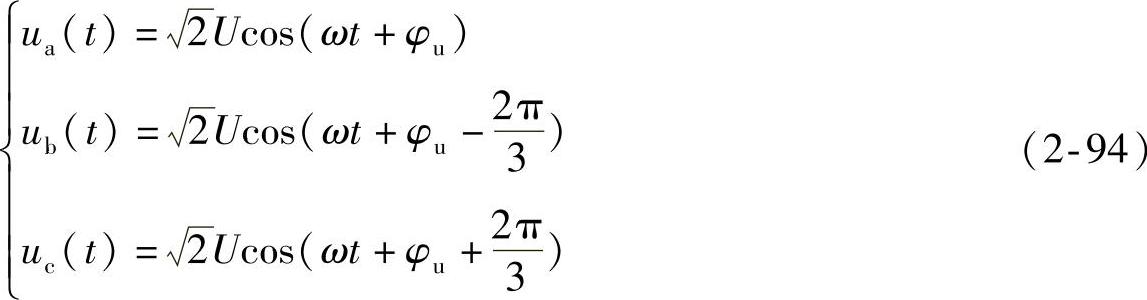
其各相线电流为

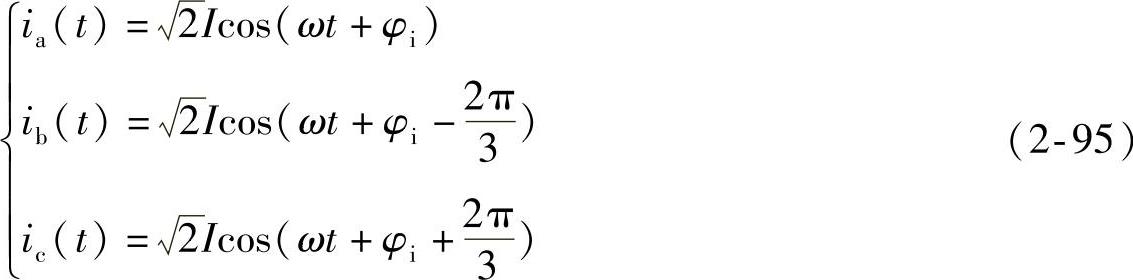
式中，φ_u和φ_i分别为电压和电流相对于某特定参考时刻的相位角。上述电压和电流仅仅由单个基波正序分量构成。因此，它们是三相对称且正弦的。利用式（2-84）和式（2-86）可将上述三相对称的电压和电流变换到αβ坐标系中，变换后可得

和

这样，就可以导出电压矢量u和电流矢量i，即(https://www.chuimin.cn)

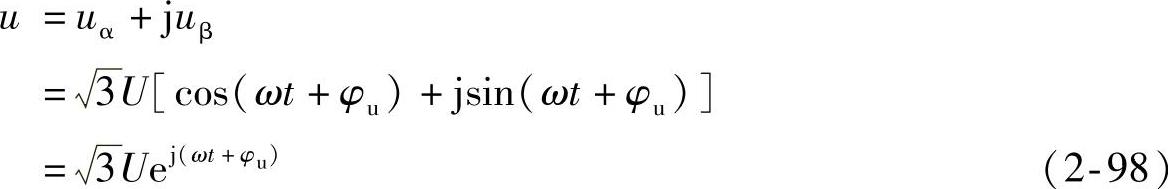
和

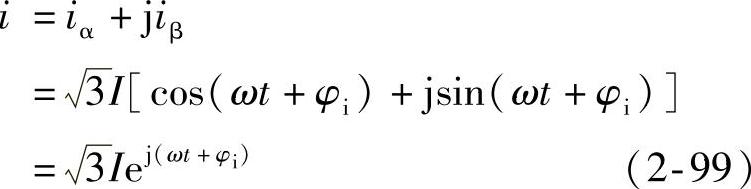
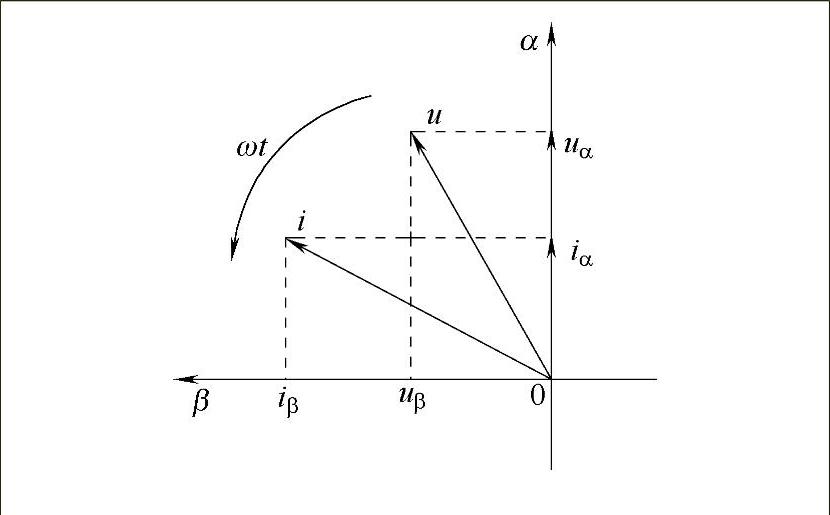
图2-11 αβ坐标系中电压和电流的矢量表示法

从上式可以看出，对于三相对称的正弦系统，电压和电流矢量的幅值是恒定的，并以角频率ω沿逆时针方向旋转，如图2-11所示。

如果将abc三相的瞬时电压和瞬时电流直接在复平面上组成电压和电流矢量，也会得到同样的结果。为了验证利用Clarke变换所得到的上述结果，a、b、c三个轴和α、β两个轴的相对位置必须保持一致，即a轴必须与复平面的实轴α轴重合，β轴是虚轴，与实轴α轴相差π/2。abc相电压中的任意一个时间函数乘以一个合适的单位相量因子后就能确定其对应轴的方向。这样，复电压矢量可以按下式来组成：

u_abc=u_ae^j0+u_be^j2π/3+u_ce^-j2π/3 （2-100）

将式中的u_a、u_b、u_c时间函数代入，并做一定的运算就能得到方程

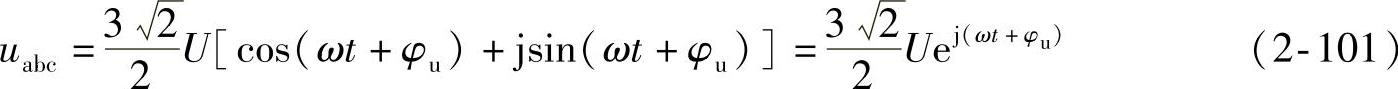
上式中的电压矢量u_abc与式（2-98）中定义的u很相像，其幅值恒定并沿逆时针方向以角频率ω旋转。因此，如果u沿逆时针方向，以同步速旋转，则u_abc也会沿逆时针方向，以同步速旋转。通过比较，可以得到如下结果：

三相瞬时电压和瞬时电流的矢量已在电力电子领域中得到了广泛应用，特别是交流传动矢量控制、功率变换器的空间矢量脉宽调制（SVPWM）以及有源滤波器等电力调节器的控制等。

电剔压除和零电序流分矢量量的测量方法

相关推荐