首页理论教育对称分量理论：从基本原理到实际应用

对称分量理论：从基本原理到实际应用

2023-06-23 理论教育版权反馈

【摘要】：但应当注意的是，由零序分量引起的不对称只能出现在三相四线制系统（接地）中，并且零序电流会流过中性线。另外，也可看出，如果各相相量仅仅由正序分量或负序分量构成，则三相瞬时电压之和以及三相瞬时线电流之和总等于零。因此，正序分量和负序分量可以存在于有中性线或无中性线的三相系统中。

现有的交流电力系统一般都是三相系统，三相电力系统中经常提到的正序、负序、零序分量是根据a、b、c三相的顺序来确定的。正序是指a、b、c三相相量、、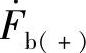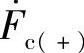，其幅值相等，相序按顺时针旋转，各相相差120°；而负序是指a、b、c三相相量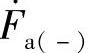、、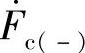，其幅值相等，相序按逆时针旋转，各相相差120°；零序则是指a、b、c三相相量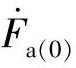、、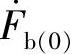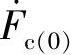，其幅值和相位均相同。三相系统中相应的正序、负序和零序的相量图如图2-8所示。

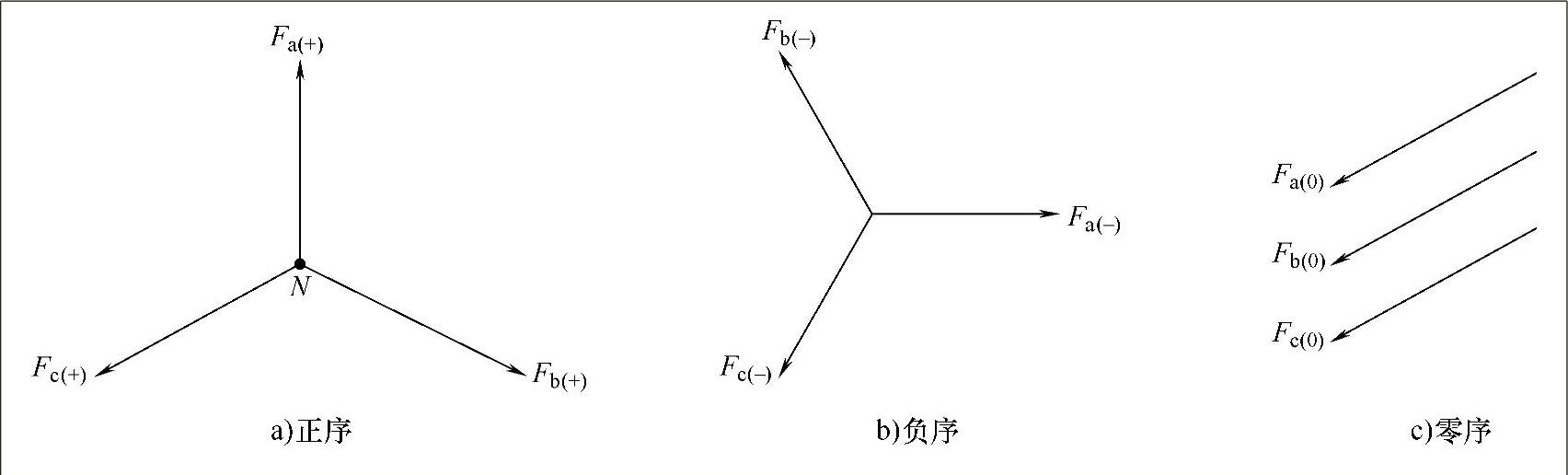
图2-8 三相系统中相序相量示意图

对于任何三相不对称相量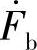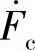（、、），根据对称分量理论，都可看作正序分量、负序分量和零序分量的叠加，如下式

由于无论正序、负序还是零序分量，每一组相量都是对称的，因此有如下关系存在：

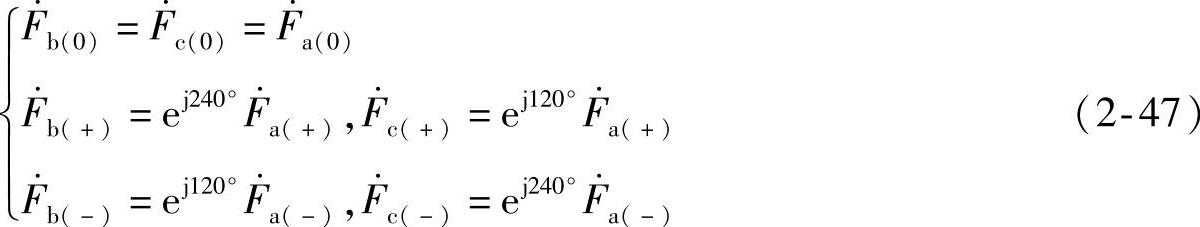
若定义复数相量因子α，且满足

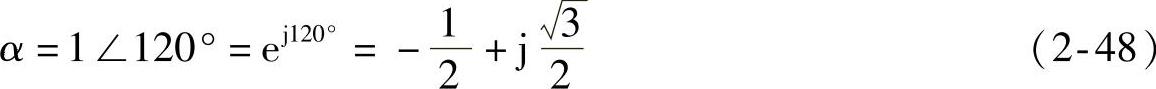
上述定义的相量因子α还满足如下方程：

1+α+α²=0，α³=1 （2-49）

将式（2-47）、式（2-48）代入式（2-46），可得

上述式子表明了三组对称相量可合成得到三个不对称相量，其反变换为

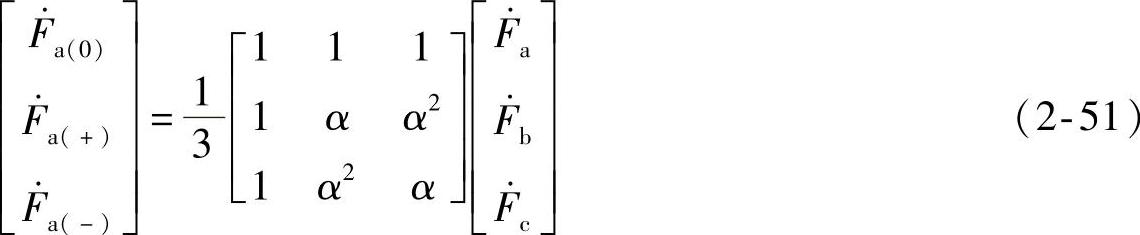
将三相系统中的线电流应用于式（2-51），可得

由此，可求出三相系统中的零序电流为

在三相系统中，若存在零序电流，则必须有中性线为其提供通路。因此，正如前面所述，三相系统中，基波频率下的不对称主要由负序或零序分量引起。但应当注意的是，由零序分量引起的不对称只能出现在三相四线制系统（接地）中，并且零序电流会流过中性线。而仅由负序分量引起的不对称，不仅可以出现在三相接地系统，也能出现在三相不接地系统中。另外，也可看出，如果各相相量仅仅由正序分量或负序分量构成，则三相瞬时电压之和以及三相瞬时线电流之和总等于零。因此，正序分量和负序分量可以存在于有中性线或无中性线的三相系统中。