首页理论教育正弦条件下功率分析法的优化

正弦条件下功率分析法的优化

2025-09-29 理论教育版权反馈

【摘要】：UIsinφsin2ωt部分是一个2倍系统频率的纯振荡分量，其峰值为UIsinφ。由上述瞬时功率表达式可知，对于单相正弦交流电力系统而言，其瞬时功率并不是恒定的，主要是在直流分量UIcosφ的基础上叠加了一个2倍系统频率的功率振荡分量。传统有功功率的定义为瞬时功率在一个正弦周期内的平均值。该物理量可被理解为用来表示在单位功率因数下可达到的最大有功功率。图2-1 功率三角形图2-1 功率三角形

在单相正弦交流电力系统中，若系统接有阻感负载，则负载两端的电压和电流表达式为

式中，U和I分别表示电压和电流的有效值；ω为系统的角频率；φ为阻感负载所导致的电流落后于电压的相位差。

此时，单相交流系统输出瞬时功率可表示为

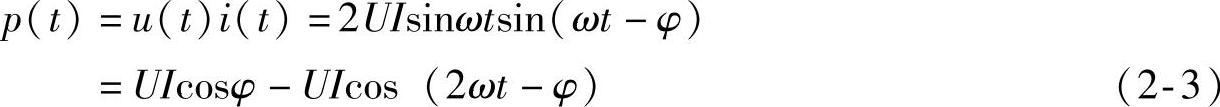
由上述瞬时功率表达式可知，对于单相正弦交流电力系统而言，其瞬时功率并不是恒定的，主要是在直流分量UIcosφ的基础上叠加了一个2倍系统频率的功率振荡分量。如果将式（2-3）中的功率振荡分量进行分解后重新整理，就可得到方程式

p（t）=UIcosφ（1-cos2ωt）-UIsinφsin2ωt （2-4）

就式（2-4）中瞬时功率的两个部分，可以做些深入的探讨和理解。

UIcosφ（1-cos2ωt）部分具有一个平均值UIcosφ和一个2倍系统频率的振荡分量。该功率部分永远不会变负，它表示了从电源到负载的单向功率流（潮流）。

UIsinφsin2ωt部分是一个2倍系统频率的纯振荡分量，其峰值为UIsinφ。显而易见，它的平均值为0。

传统上的理解，式（2-4）所表示的瞬时功率包含了传统有功功率和无功功率两个分量。传统有功功率的定义为瞬时功率在一个正弦周期内的平均值。据此，分析出瞬时功率表达式（2-4）中的第一部分表达式在一个电周期内的平均值可表示为单相正弦交流系统的有功功率，即

P=UIcosφ （2-5）(https://www.chuimin.cn)

有功功率的单位名称为瓦（W）。

而无功功率则为瞬时功率表达式第二部分的最大值，即

Q=UIsinφ （2-6）

无功功率的单位名称被定义为乏（var）。

而系统的视在功率为单相正弦交流系统的电压有效值和电流有效值的乘积，即

S=UI （2-7）

由式（2-5）～式（2-7）可知，视在功率、有功功率和无功功率满足关系

S²=P²+Q² （2-8）

式（2-8）描述的关系可用图2-1所示直角三角形来表示，这就是常说的功率三角形。

视在功率的国际单位是伏安（V·A）。该物理量可被理解为用来表示在单位功率因数下可达到的最大有功功率。

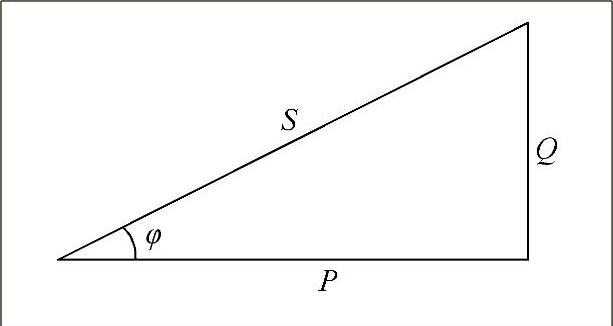
图2-1 功率三角形