电容滤波的单相桥式不可控整流电路

2023-06-23 理论教育版权反馈

【摘要】：工作原理及波形分析在小功率场合，整流部分大多采用电容滤波的单相不可控整流电路，其电路及波形如图2.35 所示。图2.35带电容滤波的单相桥式不可控整流电路及波形基本数量关系1）输出直流电压平均值Ud空载时，相当于开路，R=∞，电容不放电，一直保持u2 峰值不变，重载时，电容放电很快，几乎失去了保持的作用，ud 跟着u2 变化，ud 波形与电阻负载不可控整流电路相同，直流电压平均值Ud=0.9U2。

（1）工作原理及波形分析

在小功率场合（例如在计算机、电视机等家电产品中所采用的开关电源），整流部分大多采用电容滤波的单相不可控整流电路，其电路及波形如图2.35 所示。

假设电路已稳定工作，由于在实际中流过后级电路（负载）的电流平均值是一定的，故在下面的分析中以电阻R 作为负载进行分析，如图2.35（a）所示。将时间坐标ωt=0 的时刻定在负载电压ud 与电源电压u2 正半周交点对应的时刻，参照图2.35（b）。在电源电压u2 正半周过零点至ωt=0 期间，因为u2<ud，故整流二极管都不导通，此阶段电容C 向负载电阻R 放电，为负载提供电流，同时负载电压ud 逐渐下降。至ωt=0 之后，u2>ud，整流二极管VD1 和VD4 因受正向电压开始导通，ud=uc=u2。此时，电源电压u2 一方面向电容充电，另一方面向负载R 供电，负载电压ud 又开始随着u2 上升。当u2 达到峰值后，开始回落，只有当u2 因下降太快（快于电容放电速度）而不能维持VD1 和VD4 导通时，id 减小为零，此时ωt=θ，如图2.35（c）所示。之后ud 靠uc 来保持，保持的情况与电容的大小及负载的大小有关，负载越大（即R 的值越小），ud 下降越快。ud 按指数规律下降，时间常数为RC。这个区间如图2.35（b）中的θ 到π 这一阶段，与前述的u2 正半周过零点至ωt=0 的区间相同。下一个波头的工作情况发生在电源电压u2 的负半周，另一对二极管VD2 和VD3 导通，与上面所分析的u2 正半周的工作情况相同，不再详细介绍。可见，每个波头电压波形分两段：第一段电容充电，二极管导通，id 不为零；第二段电容放电，二极管不导通，id 为零。

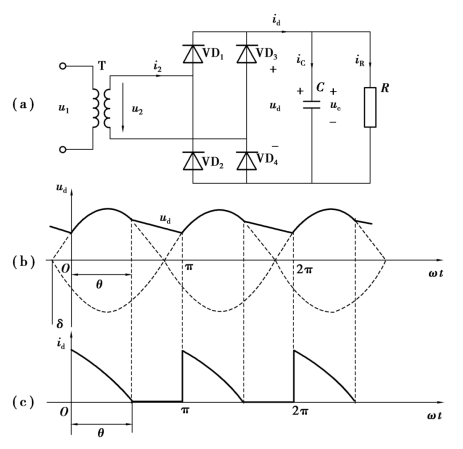
pagenumber_ebook=98,pagenumber_book=91

图2.35　带电容滤波的单相桥式不可控整流电路及波形

（2）基本数量关系

1）输出直流电压平均值Ud

空载时，相当于开路，R=∞，电容不放电，一直保持u2 峰值不变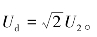，重载（R 很小，接近短路）时，电容放电很快，几乎失去了保持的作用，ud 跟着u2 变化，ud 波形与电阻负载不可控整流电路相同，直流电压平均值Ud=0.9U2。

除负载R 外，电容C 的大小同样影响ud 的保持情况。电容C 越大，放电速度越慢，ud 越稳。一般根据负载的大小选择电容C 的值。通常满足RC ≥（3～5）T/2，其中T 为交流电周期，此时输出电压

2）二极管承受的电压

从前述波形分析可知，二极管可能承受的最大反向电压为变压器二次相电压的峰值，即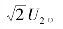

以上分析的是电路稳定时的工作情况。电路刚上电时，由于电容两端电压为零，会形成较大的冲击电流。为了抑制这个电流，在实际应用中，常在整流电路与电容之间串入电感，成为感容滤波电路。此时输出电压ud 变得更加平直，同时负载电流id 的上升段不再陡峭，这对于负载和整流器件的正常工作是有利的。当C 与L 的取值变化时，电路的工作情况也会相应发生变化。

电容滤波的单相桥式不可控整流电路

相关推荐