当其他公司都在努力研发新一代冷轧管机的时候,D.M.S公司致力于研制具有更高可靠性和生产率的1LPR型轧管机。DMS公司1LPR型冷轧管机其创新点主要包括以下方面。1LPR型D.M.S单线冷轧管机每个扇形块平衡由轧机机架往复运动所产生的水平惯性力的一半。无论曲柄轴的角度如何变化,都可以在电机与轧管机机架之间通过半个万向联轴节来平衡惯性力矩。法国D.M.S公司1LPR型D.M.S单线冷轧管机的主要优点如下。表2-13法国系列冷轧管机的主要技术性能......
2023-06-23
一台冷轧管机,无论它的机构设计得多么完美,如果它的轧制工具没有合理地设计,那么就不能充分发挥它的作用。因此,在生产应用中,冷轧管机的用户对冷轧管机的孔型设计无不给予高度重视。从本质上可以说,冷轧管机的孔型设计是一台冷轧管机的灵魂。
轧制工具的设计直接关系到产品的产量,如成品的尺寸及公差、表面状态、成品管的形状、轧机的产能和轧机主要零部件的使用寿命,这些都是轧管机孔型设计必须追求的。
一个好的孔型设计还必须遵循金属变形的规律,如合理的减径量、壁厚压下量、延伸系数、送进量、管坯的转角、变形区各段应有的长度以及充分的冷却和润滑条件等,只有将这些因素都充分考虑周全,孔型设计的结果才是最佳的。
目前,孔型设计的方法有多种,每种方法均有各自的理论基础。
4.1 Ю.Ф.Шевакин 孔型设计方法
该方法的基础是沿变形区的长度实现相对变形。该变形区可以实现较大的减径量(在减径区),而壁厚在较小的芯棒锥体上实现变形。它的优点是孔型的宽度较小,变形不均匀度减小和较好的成品管表面质量。
孔型设计的原则是:在孔型工作段开始时将进行较大的直径减径,在工作段的其余长度上进行管坯壁厚的减壁,同时还实现较小的直径减径。也就是说壁厚的变形是在锥度较小的芯棒上进行的。因此,我们将冷轧管时的变形分成两部分,即管坯直径的减径和管坯壁厚的减壁。因为在直径减径时金属对轧辊的压力很小(仅为壁厚压下时轧制压力的5%~15%),所以可以在较短的孔型工作段完成管材的减径。但在确定孔型压下段的形状时,必须考虑管材在减径时的壁厚增量。
(1)孔型形状的计算
![]()
式中 lp——壁厚压下段长度;
t0——管坯原始壁厚(含减径时壁厚的增量);
μt——管坯原始壁厚(含减径时壁厚的增量)与成品壁厚之比;
n——系数,n=0.5-0.64 n=0.5—对于铝合金n=0.5;其他金属n=0.64。
按锥体的横断面积的变化计算孔型时,可用下式计算:
![]()
式中 μΣ=Fο/Fc
(2)或用下式计算
![]()
式中 tο——管坯的壁厚,包括减径时壁厚的增量,tο=tP+Δtj。
4.1.1 减径区管坯的壁厚增量
根据大量的试验结果,在实际的计算中可采用下列方程求出管坯在减径时的壁厚增量:
![]()
式中 tp——管坯壁厚;
ΔDj——直径减径量;
DP——管坯直径。
4.1.2 孔型宽度的确定
在孔型设计时必须确定芯棒尺寸,选择孔型工作部分的长度并将孔型分区,确定孔型减径段长度,计算孔型的形状和开口值。
确定上述孔型设计参数的合理方法是从计算孔型的宽度开始,也就是从金属变形在瞬时变形区的变形开始。
冷轧管的实际经验显示,孔型开口与成品管的质量及轧机的产量有直接的关系。如出现飞刺、压痕及粘辊等,均与轧辊孔型开口不足有关。如果不改变孔型宽度,那么只有减小送进量,降低轧机的生产能力;如果开口过大,将会在成品的表面出现纵向和横向裂纹,几何尺寸变坏并导致废品。因此,确定孔型宽度是孔型设计的一个重要内容。
孔型的宽度由下式确定:
![]()
式中 Dx——计算断面锥体直径,它等于孔型深度加上辊缝间隙;
Kn——决定金属宽展的系数Kn=0.15-0.20;
A——在辊缘没有压下的情况下的宽展量;
Kj——减径系数Kj=0.9~1.15;
B——管子内径的增量。
二辊和三辊冷轧管机孔型宽度计算分别示于图2-127、2-128。
(1)二辊式冷轧管机,在预均整段结束时和均整段开始时,孔型宽度的确定如下式

图2-127 二辊冷轧管机孔型宽度计算示意

图2-128 三辊冷轧管机孔型宽度计算示意
![]()
式中 Dc——成品外径;
m——送进量;
μΣ——总延伸系数;
tgryj——预均整段变形区难度。
如图2-127所示,在加工孔型时,孔型的开口角为:
![]()
开口的深度为:
![]()
(2)三辊式冷轧管机,孔型的宽度的计算
![]()
式中 K2——是确定在瞬时变形区中金属的宽展和管的椭圆度,K2=1.10~1.15;
Δtx——均整段机架弹性变形。
4.1.3 孔型的深度
![]()
4.1.4 孔型开口角
![]()
4.1.5 孔型开口深度
![]()
4.1.6 芯棒锥度的确定
按Ю.Ф.Шевакин孔型设计方法,它主要采用锥形芯棒,如图2-129所示。使用锥形芯棒允许改变芯棒相对于孔型的位置,其目的是改变成品管的壁厚。因此,芯棒的锥形部份不一定必须与孔型开始部份相对应,但必须使芯棒锥度准确与孔型相对应。
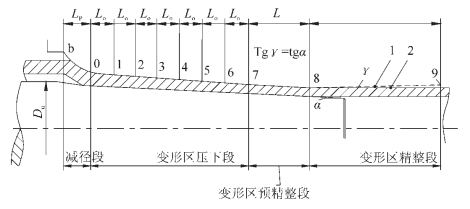
图2-129 孔型工作段长度分段及芯棒在变形区中位置示意
1—孔型开始位置上产生的均整段 2—工作段上产生的均整段
(1)芯棒锥度的计算
![]()
式中 lP——孔型工作段长度(不包括均整部分);
Dy——芯棒圆柱部分直径;
Dc——成品管外径;
tc——成品管壁厚。
(2)芯棒圆柱部分尺寸
![]()
式中 Dy——管坯外径;
tP——管坯壁厚;
Δ——管坯内径与芯棒圆柱段的间隙,便于芯棒自由通过管坯。
孔型槽的形状,按公式进行计算。
若采用小锥度,则将孔型的开口度明显减小。但它将导致脱棒力的增大并会增加两根管坯相互插入的危险。
4.1.7 孔型减径段锥度
图2-129明确显示变形区的分段。。
变形区分为:减径段、压下段、预均整段和均整段。
一般情况下,孔型减径段的锥度不要超过2tgrjj=0.180~0.220。
4.1.8 孔型减径段的减径量
大多数情况下,减径段的直径减径量为6~12mm,而对于塑性差的金属应当很小,一般是1~2mm。
如果知道减径段孔型的锥度和直径减径量,那么就可确定减径段的长度:
![]()
若考虑到减径时壁厚的增量,则减径段长度按下式计算:
![]()
式中 DP——管坯外径;
tP——管坯壁厚;
ΔDj——减径段减径量;
Dy——芯棒圆柱段直径;
ri——变形锥体减径段锥角;
α——芯棒锥角。
4.1.9 预均整段长度
在预均整段实现成品管壁厚的轧制。
(1)预均整段孔型系数:
![]()
式中 Vyj——预均整段体积;
Vm——送进体积。
(2)预均整段的长度
![]()
一般情况下,n1=1.0-1.4,n1=1.4用于轧制高精度壁厚管材。
4.1.10 均整段长度
成品直径的孔型设计系数Π2=1.5-3,若芯棒锥度越大,则孔型系数Π2就越大。
均整段长度:
![]()
4.1.11 压下段长度
![]()
式中 lg——孔型工作段总长度;
lyj——预均整段长度;
ljz——均整段长度。
压下段长度可用下式表示:
![]()
对于厚壁管或者中间产品的管材,压下段长度为:
![]()
4.2 德国MEER公司孔型设计
德国MEER公司不仅设计制造了性能优异的高速冷轧管机,而且还开发了冷轧管机的孔型设计方法并得到了广泛的使用。这种方法用途广泛,适用于各种型号的皮尔格冷轧管机并可轧制各种材质的管材。这种孔型设计方法不但包括孔型底部的曲线形状和芯棒的形状,而且还包括孔型截面形状的确定,如孔型的开口度、轧辊孔型中心相对于辊子中心的偏移量等。
孔型的壁厚压下段可以根据实际需要分成若干等份,一般情况下分成40等份,也可以根据具体情况的需要任意增加等份数量,此时孔型的精度将会相应提高。
该设计方法使用很方便,芯棒形状曲线是孔型槽长度的函数,孔型槽底部曲线是孔型槽长度的函数。此外,它还可以确定孔型截面的尺寸。图2-130示出了孔型设计的原理。
4.2.1 变形锥体及孔型槽的计算
![]()
式中 Dx——孔型压下段“x”处锥体直径;
Cx——孔型和芯棒形状曲线系数,Cx=(x/ly)n;
n——对于黄铜、铜、铝等n=2.5-2.8,对于钢n=3.38;
DP——管坯外径;
Dc——成品管外径;
Zm——最小的芯棒锥度(此值对于轧制不同的材质其差异极大):采用曲线芯棒轧制、铜、黄铜、铝等时为0.25%,轧制钢时为2.3%,采用锥形芯棒时为3.55%;
Si——管坯内径与芯棒圆柱端直径之差,此值取0.8~1和2mm;
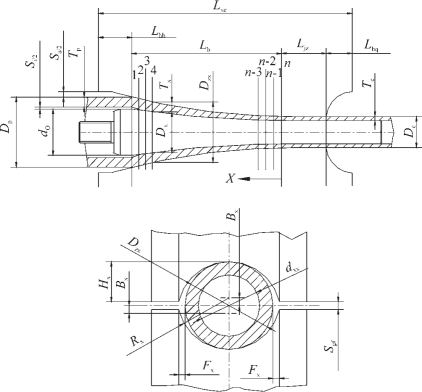
图2-130 二辊冷轧管机孔型设计示意
Sa——管坯外径与孔型底部直径间在X/ly=1时之差,一般取1~2mm;
nx——管坯内壁与芯棒间以及管坯外径与孔型最大直径之间差值的修正系数。
4.2.2 芯棒形状的计算
![]()
式中 dx——在坐标“x”处的芯棒直径;
cx——孔型和芯棒形状曲线系数;
dP——管坯内径;
dc——成品管内径,实际上芯棒应比管子内径略小一点才能保证成品管的内径尺寸,一般小0.1mm;
zm——芯棒要求的最小锥度。
上式表明,芯棒尺寸的变化与管坯及成品管外径的变化无关。
如果考虑轧辊孔型与不同芯棒配对时,那么计算孔型槽底部曲线和芯棒的曲线要注意以下方面。
(1)公式(1)和(2)中采用相同的系数cx。
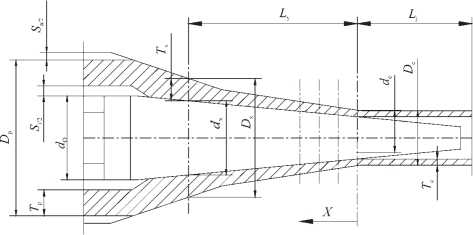
图2-131 锥形芯棒孔型设计示意
(2)若要求芯棒具有较小的锥度z,则在式(1)和(2)中必须采用相同的锥度。如果最小的锥度Zm=0,那么公式中的ly·zm就消失了。
(3)孔型的长度必须与同步齿轮的节圆直径匹配。上述计算公式适用于抛物线形芯棒。原则上来讲,它们也可以用锥形芯棒,此时可以简化如下的4.2.3所述。
4.2.3 采用锥形芯棒的孔型设计
变形锥体的计算:
![]()
芯棒的计算:
![]()
式中 K——锥形芯棒的锥度。
4.2.4 同步齿轮直径的确定
要确定同步齿轮的节圆直径,首先要确定轧制直径:
![]()
将轧制直径与同步齿轮节圆直径比较后取整值:
![]()
4.2.5 变形区中锥体壁厚的变化
![]()
(1)孔型开口值Fx的计算
孔型开口值Fx的计算如图2-132所示。

图2-132 孔型开口值Fx的计算
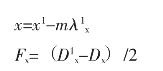
(2)变形区中壁厚的变化
![]()
(3)孔型中心与管材中心的偏移量
![]()
(4)孔型半径Rx
![]()
(5)孔型深度Hx
![]()
(6)均整段结束时的孔型半径
![]()
Rjk——均整段开始时的孔型半径;
Rjz——均整段终了时的孔型半径。
![]()
PΣ——总轧制压力。
![]()
(7)计算断面的锥体锥度
![]()
(8)计算断面的芯棒锥度(曲线芯棒)
![]()
(9)计算断面延伸系数
![]()
目前,我国二辊冷轧管机的孔型设计大部分采用德国MEER公司的孔型设计方法。但应指出的是,MEER公司的孔型设计方法中没有考虑减径时管坯壁厚的增量,这是它的一个明显的不足之处。
4.3 LD型多辊冷轧管机的孔型设计
4.3.1 孔型设计须考虑其特殊性
多辊冷轧管机孔型设计的基本原理与二辊冷轧管机无多大差别。但因轧管机的结构和轧制变形过程与二辊冷轧管机有较大差别,因此,孔型设计时必须考虑它的特殊性。
图2-133、图2-134、图2-135分别是LD多辊冷轧管机的轧辊及摇杆机构示意图、多辊冷轧管机变形区示意图和滑道的工作示意图。
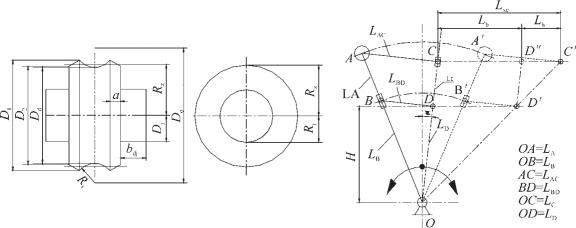
图2-133 LD多辊冷轧管机摇杆系统示意图
图2-133中的C点是轧管机的机架上的一点,行程是CC′=Lxc,D点是轧辊保持架上的一点,其相对于变形区的行程是DD′=Lb,D″C′是轧辊相对滑道(机架)的行程,D″C′=Lh。
如图2-134和图2-135所示,变形区和滑道的分段数相对应。
(1)轧辊相对于变形区的行程Lb,其分段如下。

图2-134 多辊冷轧管机变形区示意图
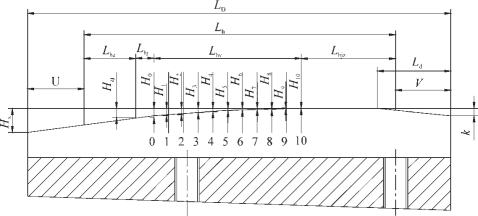
图2-135 多辊冷轧管机滑道示意图
①变形区回转送进段长度
![]()
式中 Lz为机架行程Lxc中的回转送进段长度。
②变形区减径段长度为Lbj。
③变形区壁厚压下段长度为Lby。
④变形区均整段长度为Lbjz。
⑤变形区均整段中倒锥段长度为Lbjzd。
(2)滑道分段
因滑道是变形工具,其分段与变形区的分段完全相对应,数量相同,但其长度不同。
①滑道上回转送进段长度
![]()
式中 Rj——轧辊的辊颈半径;
Rz——轧辊的轧制半径,对三辊型Rz=Rd+0.2Rc,对四辊型Rz=Rd+0.1Rc;
Rd——轧辊孔型底部半径,Rd=(Dο-Dc)/2。
②滑道上减径段长度
![]()
减径段倾角tgγhj<(0.18-0.22)。如果大于这个范围,将会产生较大的轴向力,容易将管子从变形区中推出,造成轧制事故。
③滑道上壁厚压下段长度
![]()
④滑道上均整段长度
![]()
⑤滑道上均整段中倒锥段长度
![]()
在滑道上必须有这个倒锥段,否则将在成品表面出现凸起式的鱼鳞斑,造成废品,其长度为10~15mm,高度为0.5~0.8mm。
(3)滑道壁厚压下段中壁厚压下量的计算
应该说明的是,变形区中壁厚变形量的分配直接关系到产品的质量和轧机的生产能力,影响到工具的磨损和使用寿命。
多辊冷轧管机轧制时变形量的分配可按Ю.Ф.Шевакин方法计算。
如图2-105所示,若将滑道的壁厚压下段分成10等份,如图2-134,多坯冷轧管机变形区中管坯壁厚的变化按下式计算:
![]()
式中 Lhy——滑道壁厚压下段长度;
tο——管坯的壁厚与减径时壁厚增量之和,tο=TP+Δtj
Δtj=(0.7~0.8)·TP·(ΔDj)/DP;
TP——管坯壁厚;
ΔDj——外径减径量;
DP——管坯外径;
μt=tο/Tρ——按壁厚计算的延伸系数,n=0.5-0.64,对于铝合金n=0.5,对于其他金属n=0.64;
Lhy——滑道壁厚压下段长度。
一般情况下,滑道壁厚压下段可被分成7~10等份,甚至还可更多等份,这样会延长滑道的使用寿命,金属的变形会更加均匀合理。
4.3.2 轧辊的孔型设计
(1)多辊冷轧管机最佳轧辊的尺寸
В.В.Носаль给出了多辊冷轧管机最佳轧辊的尺寸,其中包括轧辊孔型底部直径、成品管的孔型半径、轧辊辊颈的直径和长度及孔型侧部的厚度。
①最佳孔型轮缘厚度
![]()
式中 a——孔型侧面厚度;
Rc——成品管半径;
n——轧辊的数量。
②轧辊辊颈的长度

(2)许用接触应力的计算公式
В.В.Носаль同时给出了许用接触应力的计算公式:
![]()
(3)辊颈的半径
![]()
用此公式尚不能保证辊颈的刚度和强度。为此,提出下列公式。

(4)孔型底部的最大直径
![]()
式中 f——摩擦系数。
孔型底部直径:
Dd=Dο-Dc
式中 Dc——成品管直径。
(5)轧管机的调整
如图133所示,摇杆系统中的相互关系如下:
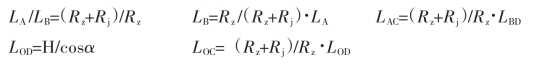
有关精密管材生产工艺技术的文章

当其他公司都在努力研发新一代冷轧管机的时候,D.M.S公司致力于研制具有更高可靠性和生产率的1LPR型轧管机。DMS公司1LPR型冷轧管机其创新点主要包括以下方面。1LPR型D.M.S单线冷轧管机每个扇形块平衡由轧机机架往复运动所产生的水平惯性力的一半。无论曲柄轴的角度如何变化,都可以在电机与轧管机机架之间通过半个万向联轴节来平衡惯性力矩。法国D.M.S公司1LPR型D.M.S单线冷轧管机的主要优点如下。表2-13法国系列冷轧管机的主要技术性能......
2023-06-23

冷轧管机最初在美国发明。在二次世界大战期间,为了扩充军备,冷轧管机得到高速度发展。因此,生产新型材料的冷轧管机也以空前的速度发展。我国自行设计和制造冷轧管机始于1960年。在改革开放后,在我国浙江和江苏一带,涌现了共30余家冷轧管机的制造厂家。与此同时,不少冷轧管材生产厂家迅速增加,甚至出现了许多的家庭作坊。......
2023-06-23

我国曾于1958年由前苏联引进了ХПТ-32、ХПТ-55和ХПТ-75等三种规格的二辊周期式冷轧管机,全部是半圆形孔型块。由此填补了我国高精度高质量航空用管生产的空白,解决了我国没有冷轧管机的生产问题。上述三个单位开发的冷轧管机的主要参数分别见表2-14~17。这是目前我国自行设计、制造的最大规格冷轧管机,标志着我国冷轧管机进入了快速发展的阶段。......
2023-06-23

目前,已被广泛应用的冷轧管机共分两大类型:二辊皮尔格式冷轧管机和多辊式冷轧管机。二辊冷轧管机轧制原理及机架传动机构如图2-1、图2-2所示。这样,当轧管机机架作不间断的往复运动时,就可以完成对管坯的轧制。二辊冷轧管机和多辊冷轧管机一般由以下几个主要部分组成。图2-2冷轧管机机架传动机构1.1二辊式冷轧管机轧管机机架由曲柄连杆机构带动作往复运动。......
2023-06-23

战后大量的冷轧管机投入生产。俄罗斯1937年由乌拉尔重机厂设计制造的冷轧管机的主要参数见表2-6。俄罗斯现代的冷轧管机已是今非昔比了。它继承和发展了俄罗斯冷轧管机制造事业,先后开发了许多优秀的产品并出口到许多国家,包括中国在内。......
2023-06-23

德国开发了系列冷轧管机,各类型冷轧管机的结构特点如下所述。表2-5MEER公司开发的二辊式冷轧管机参数图2-13垂直平衡原理示意1.5MEER公司开发的高精度二辊式冷轧管机MEER公司开发的用于轧制高精度高标准的小规格的二辊式冷轧管机KPW25HMRK、KPW-18-HMRK和KPW-10。采用双扇形块平衡冷轧管机机架在高速往复运动时产生的惯性力,其效果非常好。......
2023-06-23

支管式机头结构如图6-9所示,圆筒料槽可适当大些以储存更多的熔料,使料流更稳定。支管式机头有以下几种结构形式。支管的模腔与挤出的料流方向一致,塑料板材的幅宽可用在型腔中设计的幅宽调节块按需要调节。图6-13 带有阻流棒的双支管形机头1—支管模腔 2—阻流棒 3—模口调节块......
2023-06-15

在锅炉、化工、电力及核电等领域的管线以及换热器的生产和安装中,存在大量的管-管和管-管板的焊接,通常都采用TIG焊方法。为了保证一定的余高,焊前将管端适当扩口或者添加填充焊丝,也可以用TIG焊打底后再用焊条电弧焊盖面。......
2023-06-26
相关推荐