身体的情绪地图家人都知道我有个小小的习惯——喜欢洗头发。或者，用另一个说法来解释，就是身体提供了心理问题一个“宣泄”的窗口。因此，根据世界心理卫生组织的统计，大约有70%以上有心理障碍的人会以“攻击”身体器官的方式来消化自己的情绪困扰。由此可知，除了环境污染、饮食内容、卫生习惯等等为人熟知的因素之外，情绪压力绝对在其中扮演了举足轻重的角色。......
2024-07-17
轧制压力对轧机生产的影响
【摘要】：变形区的尺寸和金属变形速度等因素决定了轧制过程的作用力的大小、轧机的生产能力和轧制工具的使用寿命。正行程轧制时，由于轧制压力的作用，机架将产生弹性变形。
3.1 冷轧管时金属变形的基本原理
冷轧管机采用2个或3个带有变断面孔型的轧辊，装在一个能承受轧制压力的框架内，由曲柄连杆机构带动作往复运动。在每一个轧辊的侧面装有一个同步齿轮，该同步齿轮与固定在机座上的齿条啮合。当机架作往复运动时，轧辊将作往复运动同时还将各自围绕自己的轴心以相反的方向同步旋转。
在轧制中心线上放置一个固定的锥形或者曲线形芯棒。当机架往复运动时，2个或3个轧辊上的变断面孔型将对管坯进行轧制，使管坯产生变形。当机架运动到后极限位置时，由送进机构将管坯向前推进一个规定的距离，称为送进量；当机架运动到前极限位置时，回转机构将管坯转动一个规定的角度，这样，当机架连续不间断地作往复运动时，就实现了轧辊孔型对管坯的有效轧制，并形成了一个锥形变形区。如图2-118所示。
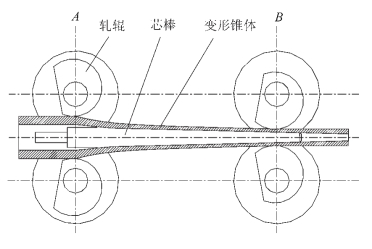
图2-118 二辊冷轧管机轧管的过程示意
在冷轧管过程中，孔型的半径和变形量的大小随着机架行程的变化而变化，这是冷轧管过程的突出特点。
变形区的尺寸和金属变形速度等因素决定了轧制过程的作用力的大小、轧机的生产能力和轧制工具的使用寿命。因此，研究冷轧管的过程，首先应分析变形区的各项参数。
3.1.1 瞬时变形区的压下量
瞬时变形区金属的压下量在皮尔格轧制理论中具有重要意义。
Π.Т.Емельяненко 是这样定义皮尔格压下量的：
由计算断面算起向反方向拉开一个距离，建一个新的断面，称为起始断面，起始断面与计算断面间的体积应等于送进体积，起始断面的高度与计算断面的高度差，即为压下量。
А.ИЦеликов和 А.Н.Ирошников均得出与此相似的结论。
假设一个皮尔格轧辊在平面上轧制（图2-119 a），被轧金属将向高度减小的方向移动，轧辊上的孔型曲线与锥体曲线不是相交于点16，而是相交于点5，点5的位置由如下条件确定：
冷轧管时，确定压下量是寻找金属在变形过程中的线性位移hx，也就是确定锥体上已知计算断面与起始断面的距离。起始断面与已知计算断面间的体积等于送进体积。
孔型在任意位置上的线性延伸可以认为是直线性的，且误差并不大。此时，壁厚的压下量由下式确定：
式中 tgrx——在该段上孔型的平均锥度；
tgα——芯棒锥度。
外径的减径量可以用下式确定：
目前，用Я.Е.Осада公式来确定每一个轧制周期的壁厚压下量：
式中 Vy——单位送进体积，Vy=m·tP［（Dp-tp）/（Dx-tx）］；
Dp——管坯直径；
tp——管坯壁厚；
m——送进量。
按上式（1）计算的壁厚压下量与实际的误差不超过2%～3%。
由 М.Б.Рогов 和 П.К.Тетерин 推导出的较简单的计算壁厚压下量的近似公式得到了广泛的应用，但它的误差较大。
式中 μx=Fp/Fx——计算断面的延伸系数；
Fp——管坯的横断面积；
Fx——计算断面的横断面积。
式（2）相当简单，实际使用中非常有价值。但它的应用受到tgrx-tgα值的制约，只有当tgrx-tgα＜0.06-0.05时可以满足要求。
式（1）和（2）是用确定一个轧制周期（即机架往复一次）的压下量，并假设送进时被送进的金属在正行程已完成全部变形。但实际上，在冷轧过程中，很大一部分送进体积是在反行程时完成变形的。
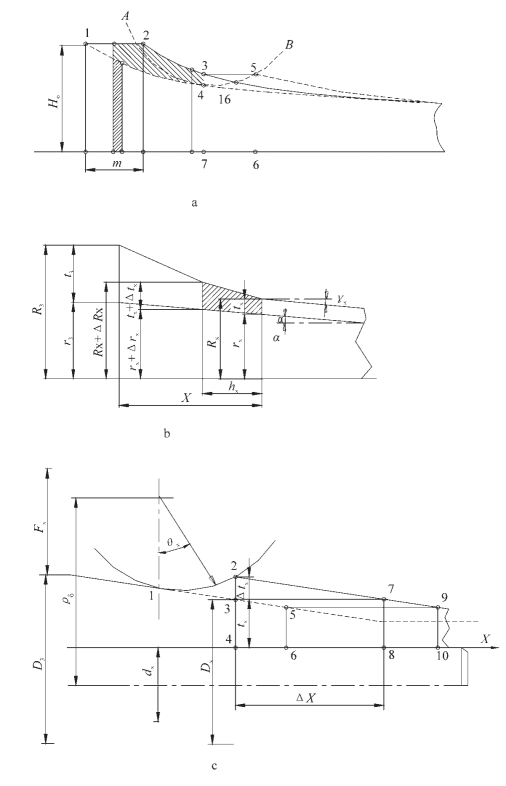
图2-119 皮尔格轧制过程的压下量确定示意
瞬时变形区中的压下量△tx由下式求出：
式中 ρx——计算断面轧辊孔型底部半径。
周期的壁厚压下量Δtz按式（2）确定。
冷轧管时，正行程和反行程时金属的变形情况并不相同。正行程轧制时，由于轧制压力的作用，机架将产生弹性变形。此外，在轧制过程中金属将向辊缝方向流动，这样就使得反行程轧制时的负荷增加。受轧制力的影响，机架仍然要产生弹性变形。为此，就有必要对公式（3）进行必要的修正。
根据大量的理论分析及试验数据验证，引入一个修正系数，用于修正正行程和反行程计算壁厚压下量：
Kt=0.30～0.40
为确定瞬时变形区的压下量，建议使用下面的简化公式：
正行程时：
Δtx按公式（3）计算。
反行程时：
3.1.2 确定金属与孔型在轧制过程中的接触面积
在皮尔格轧制过程中，金属与孔型的接触面积的特点是：变形区的形状非常复杂，接触面积很小并且沿孔型长度方向是变化的。Π.Т.Емельяненко在计算热轧皮尔格轧机的金属与孔型接触面积时，只限于计算孔型的咬入长度，近似地认为接触面积的长度沿孔型的圆周长是不变的。
首先用解析的方法解决冷轧管时金属与孔型的接触面积的水平投影的计算问题是Я.Е.Осада。他推导出了确定变形区前端边界的空间曲线方程。为求出全部的接触面积的水平投影，必须知道最大的咬入角θmax，但Я.Е.Осада并没有给出确定θmax的方程，因此该方程并不能推导出确定的结果。
Ю.Ф.Шевакин最后推导出了金属与轧辊在轧制时接触面积的水平投影。
轧辊与金属接触面积的水平投影的计算公式是：
η3为接触面积的形状系数，在1.20～1.25之间变化（用于二辊式冷轧管机）；η3=1.10（用于三辊式冷轧管机）。
对于壁厚压下区全接触面积由下列方程确定：
式（6）和（7），对于机架在正行程和反行程时均可用。
在机架的反行程前进行管坯的回转对于接触面积的影响是合理的。根据试验数据分析，在反行程前进行的管坯转角没有对轧制压力有明显影响，同样对接触面积也是如此。
反行程时接触面积的形状与正行程时的接触面积的形状完全相似并由壁厚变形区范围决定。轧制时管坯被压扁所增加的接触面积完全可以忽略不计。因此，确定接触面积就是向公式（6）和（7）代入瞬时变形区中的正行程和反行程公式（4）和（5）的压下量值。
3.1.3 轧制过程中轧辊弹性压扁时接触面积的变化
M.Б.Pогов在研究轧制过程中轧辊压扁的问题时，考虑到轧辊压扁时接触面积的水平投影。
对于二辊式冷轧管机，弹性压扁时总接触面积的增量：
式中 ρx——轧辊孔形底部半径。
弹性压扁时接触面积增量的水平投影：
对于三辊式冷轧管机，弹性压扁时总接触面积的增量：
三辊式冷轧管机弹性压扁时接触面积增量的水平投影：
3.1.4 轧制压力的计算
冷轧管时轧制压力的计算是一个非常复杂的问题，它与所轧金属的物理性能和金属的成分有密切的关系，还与轧辊孔型的形状、轧制速度、金属与轧辊孔型表面及金属与芯棒间的摩擦、轧辊在轧制过程中的弹性压扁等均有直接的关系。
研究冷轧管时轧制压力的专家也很多，所得出的结论各不完全相同。在此简要介绍常用的几种方法。
（1）冷轧管时单位压力的计算方法
① C.И.Гуδкин 公式
式中 K——真实的变形抗力；
f——摩擦系数；
ρz——轧辊孔型底部半径。
② В.Неман 和 Ε.Зивель公式
式中 σT——金属的屈服极限；
ηF——有效系数，它考虑到摩擦力的影响，对于钢为40%～60%：有色金属60%～80%；
ld——咬入弧长。
③ Ш.Г.eлеи 公式
式中 t1x=tx+0.5·Δtx；
υ——轧制速度。
④ Д.И.Пирязев公式
式中 σb——金属的强度极限；
c——系数，c=0.358。
⑤ Β.Β.Носаль公式
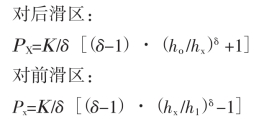
其中系数 δ，Β.Β.Носаль 用下式求出：
δ=（foпp+fΒaл）/Δtx·ld轧制钢管时，摩擦系数的综合值foпp+fΒaл=0.45
⑥ Ю.Ф.Шевакин 公式
根据对试验的结果，包括单位压力和总压力的分析，建议金属对轧辊在正行程时的单位压力如下：
反行程单位压力：
式中 f——摩擦系数，f=0.08-0.10对钢和铝合金；f=0.06-0.07对紫铜、黄铜和其他有色金属；
to——管坯的壁厚（包括减径段壁厚增量）。
减径时单位压力：
式中 ρx——轧辊孔形底部半径；
ρTB——轧辊同步齿轮节圆半径。
（2）轧制时金属对轧辊的总压力
①正行程金属对轧辊的总压力
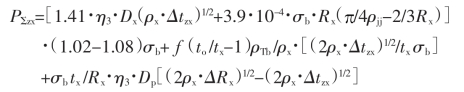
②反行程金属对轧辊的总压力
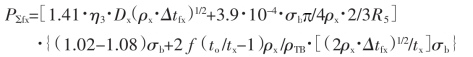
减径时单位压力所占比重不大于10%（与壁厚压下段相比），因此在实际计算中，减径段的单位压力忽略不计。冷轧管时金属机械性能的变化与变形程度的关系如图2-120所示。
机架反行程时，减径段实际上不存在。
ХПТ450轧机金属对轧辊总压力计算例题：
送进量m=10，孔型图按图2-122，计算金属对轧辊的总压力，计算断面3的轧制压力。
③瞬时变形区的压下量的确定
a.断面3的延伸系数
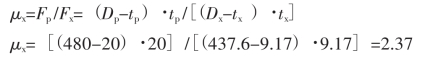
b.一个轧制周期的壁厚压下量（按公式）
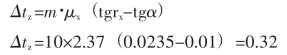
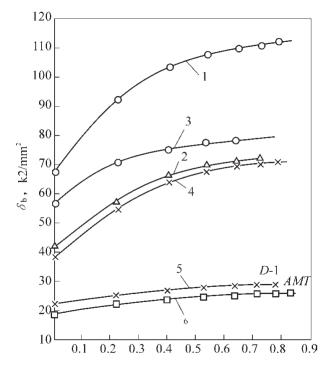
图2-120 冷轧管时金属机械性能的变化与变形程度的关系
1— 不锈钢1Сr18Ni9Ti 2—10号钢 3— 合金ВТ-1Д 4—黄铜68 5—合金Д1 6—合金AMr
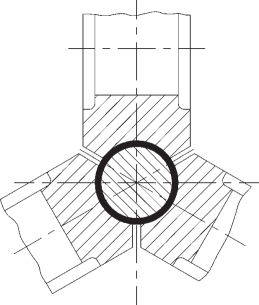
图2-121 三辊冷轧管机轧辊布置示意
c.正行程瞬时压下量
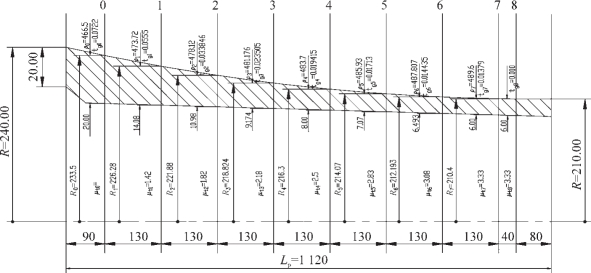
图2-122 ХПТ-450（三辊）轧制Φ480mm×20mm→Φ420mm×6mm时的孔型尺寸
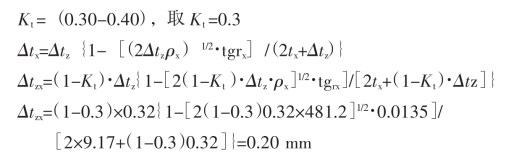
d.确定金属的强度极限σb：
当 ε=1-1/μx=57.6%，σb=114kg/mm2
e.求出接触面积的水平投影并包括弹性压扁
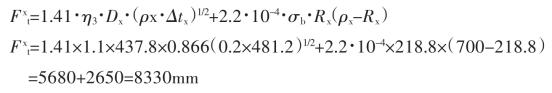
f.金属对轧辊的正行程单位压力按下式求出
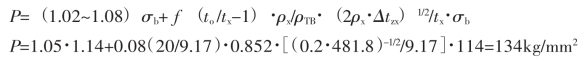
摩擦系数f=0.08。
g.总压力（不含减径段）的确定
h.减径时的单位压力确定
Pjj=σb·tx/Rx——减径时的单位压力
3.1.5 冷轧管时轴向力的计算
冷轧管金属变形时的轴向力在很大程度限制了轧管机的生产能力。在轧制过程中，一种现象是管坯因轴向力被压成波纹状；另一个严重现象是两根管子接头时互相插入，不仅影响产量还会产生过载造成严重机械故障。同此，应仔细分析研究和计算轧制时轴向力的大小。轧制压力合力方向如图2-123所示。机架返行程时变形区中的作用力如图2-124所示。
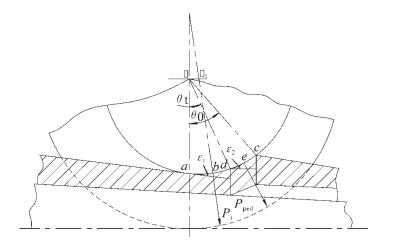
图2-123 轧制压力合力方向示意
（1）正行程时的轴向力
① 当 ωx＜Qt时
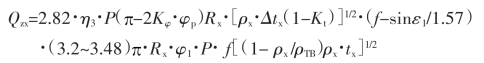
式中 咬入极限角ωx=（1.60～1.75）［（ρTB-ρx）·tx/（ρx-ρTB）］1/2
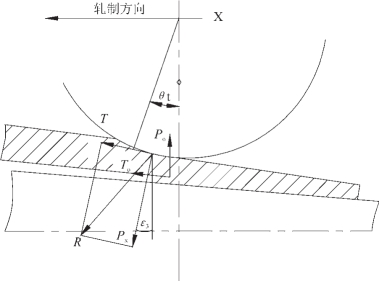
图2-124 机架返行程时变形区中的作用力示意
式中 φ1=arccos［（ρo-ρΤΒ）/RΤΒ］
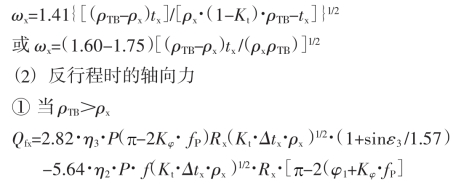
式中 Kt=0.3～0.40；
η2=1.16。
② 当 ρTB＞ρx
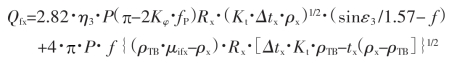
轧制压力（壁厚压下区）的合力与垂直线间夹角：
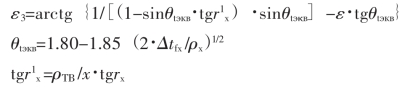
△tfx——反行程壁厚压下量。
机架返行程时确定极限角示于图2-125。
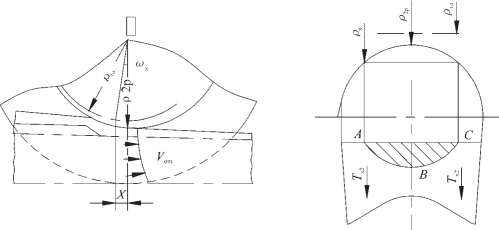
图2-125 机架返行程时确定极限角示意
（3）三辊皮尔格冷轧管机轴向力
①正行程
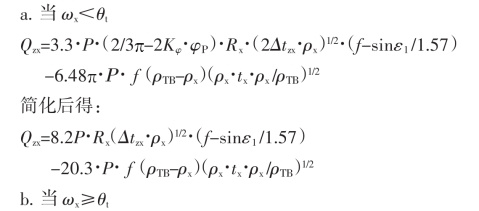
②反行程
注：计算反行程轴向力时必须注意Kφ=1.0；
在正行程时，孔型开始段Kφ=0.5，而在孔型尾部Kφ=0。
（4）二辊式冷轧管机的ρΤΒ和 λ1、λ2
①正行程
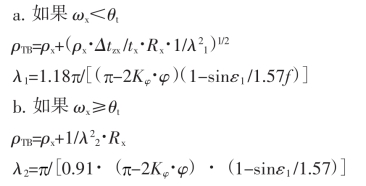
②反行程
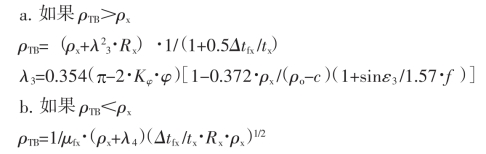
（5）三辊式冷轧管机的ρTB和λ1、λ2
①正行程
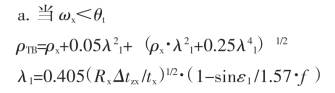
为了便于实际的计算，建议将公式简化为：
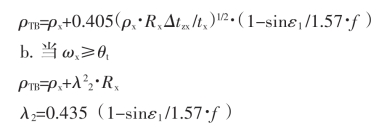
②反行程
先确定α值：
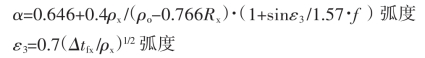
知道α，求同步齿轮的ρTB：
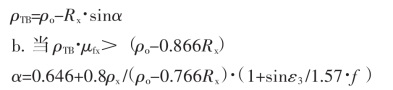
上述的计算理论推导的比较多，其中有很多修正系数，它们的取值对计算结果影响很大。对于各种计算结果的精确度很难给予正确的评价。但必须充分肯定的是俄罗斯学着Ю.Ф.Шевакин教授在冷轧管方面的功底是很深厚的，他所作的理论探索和实践经验是冷轧管方面的宝贵财富。
在机架反行程时，所产生的轴向力比正行程时的轴向力要大很多。轴向力的压缩力与轧制压力成正比。轴向力过大会导致出现工艺问题：如成品管的端部插入、芯棒杆轴向弯曲、变形锥体轴向移动，很大的轴向拉力使管坯在送进时脱离芯棒，进而造成严重的工艺和机械的恶性事故。
在轧制过程中，管坯承受的轴向力的大小在很大程度上决定了轧管机产量及产品的质量。为此，为了减轻计算的劳动强度，建议采用如下方法进行轴向力的粗略计算以可满足实际使用的须要。即反行程的轴向力是总压力的10%～15%，而正行程的轴向力是总压力的6%～10%。这个结果是经过大量的理论计算及其实践结果的比较得出的。
3.1.6 轧制力矩的计算
我们分析了在瞬时变形区中（正行程和反行程）作用力的情况。一般情况下，瞬时变形区中作用的力在水平轴上的投影径向力和切向力是相互不平衡的。因此，为金属变形所需的扭矩，扣除消耗在摩擦和动能之外，主要消耗在金属变形时轧辊的总压力的垂直分力扭矩和切向力的扭矩。金属对轧辊的总压力ΡΣ法向作用在接触面积上并经过孔型的中心Ο1，该中心相对于轧辊中心Ο有偏移。总压力的水平分力ΡΣx包括在总切向力QΣ之中。如图2-126所示。
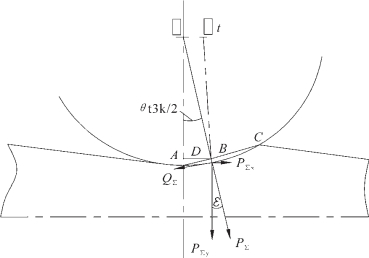
图2-126 确定轧制力矩示意
根据图2-126，作用在变形区中力的分布，轧制总扭矩对于二辊式冷轧管机，正行程的扭矩是：
如果轴向力在正行程时的方向与机架的运动方向相反（轴向压缩力），那么轴向力的扭矩将与轧制力的扭矩相加。如果轴向力与机架的运动方向相同（轴向力的负值），那么总轧制扭矩是轧制压力扭矩与轴向力扭矩之差。
对二辊式冷轧管机最终轧制扭矩的计算公式：
对二辊式冷轧管机反行程轧制扭矩按下式计算：
如果切向力的方向与机架的运动方向相同，那么轧制总扭矩是扭矩之差。若轴向力的方向与机架的运动方向相反，则总轧制扭矩是扭矩相加总和。
对三辊式冷轧管机总轧制扭矩按下式计算：
有关精密管材生产工艺技术的文章
- 详细阅读
-
《金球》节目揭示压力对人类行为的影响详细阅读
一档真实的英国电视节目——《金球》，就是根据这个前提设计的，测试人们信任和自私的底线。而没有经受压力考验的控制组，信任和可信的比例与《金球》节目的玩家十分接近——约50%。如果你认为压力总会制造或战或逃的反应，这些人的行为就无法解释。心血管系统的改变，荷尔蒙比例的释放，以及压力反应的其他方面，变化范围很广。和熟悉的或战或逃一起，这些组成了你的压力反应指令表。......
2024-01-19
-
答题王者：群体压力对从众行为的影响详细阅读
一般来说，群体规模越大，持有一致意见或采取一致行为的人数越多，则个体所感到的心理压力就越大，也就越容易从众。而如果群体中另外还有一个人持不同意见，则使前者所面临的从众压力大大缓解，从而明显降低了从众的程度。A.黑带B.红白相间的带子C.红带④知识点：1～5段系黑带，6～8段系红白相间的带子，9～10段系红带。......
2023-08-01
-
1924年杜邦硝基漆的问世及其对汽车生产的影详细阅读
1924年，杜邦公司研制出世界上首先使用喷枪喷涂的汽车漆DUCO杜邦硝基漆，从而将每辆汽车的油漆时间缩短到几小时，使汽车的批量生产成为可能，加快了汽车生产的步伐。此后，汽车漆的发展日新月异。同时珍珠漆的涂装技术进一步改进，使用二层涂装和三层涂装，使车身的颜色更加美丽。同时，色母涂料的推广，不含异氰酸酯的底涂层罩透明层的安全型聚氨酯高温烤漆等一批高科技涂料的相继问世，为21世纪汽车漆的发展开创了美好的前景。......
2023-09-29
-
侧压力系数及其对挤压性围岩隧道的影响详细阅读
由图可见，当k小于1时，随着侧压力系数的增加，拱顶沉降先减小，当k大于1时近似线性增大。而水平收敛则随侧压力系数的增加而近似以指数形式增加。随着侧压力系数k的增大，塑形屈服由节理面屈服主导向岩体剪切破坏转化。图3.5不同侧压力系数时围岩塑性区分布......
2023-09-21
-
影响你一生的心态与细节情绪对创造力的影响详细阅读
是成就大事者不断勉励自己的成功箴言。让上司放心的就是你这份积极的心态，影响上司的也是这份心态。人们对待工作的不同态度，产生着不同的结果。她们以积极的心态做着各种事，并从中感受到乐趣。看着她们以轻松愉悦的心情做事，看着她们那发自内心的满足，真是一种享受。换句话说，她是以三心二意的手艺人心态在做事，而不像前面提到的家庭主妇，完全以艺术家的心态在做家务。约翰·密尔这段话的意思是：勤奋工作是快乐的源泉。......
2023-12-06
-
液体中的密度和压力涨落现象及其对熵增定律的影详细阅读
与此相似，尽管不那么明显，液体中也同样发生密度涨落和压力涨落。当液体越来越接近沸点时，密度涨落也越来越明显，以致液体呈乳白色。我们不禁要问，对于这种涨落占主导地位的小物体，熵增定律还起不起作用？不过，我们应该看到，这时熵增定律已经失去了它本来的意义，而不应该认为这个定律不正确。[15]1微米等于0.000 1厘米，“微”常用希腊字母μ表示。......
2023-08-05
-
机油压力对VVT系统的影响和汽车维修经验与技详细阅读
在两个凸轮轴链轮的中间安装有由机油压力驱动的链条张紧器。该链条张紧器与凸轮轴调节器为一体，依靠发动机运转后的机油压力绷紧链条。奥迪A6L 2.0L BPJ发动机ECU控制凸轮轴正时调整阀N205，N205改变调整机构内的机油流动方向，从而改变配气相位，提前或延迟进气门打开的时间，以满足发动机在不同工况下的要求。原来是由于机油滤清器内密封不严，导致机油压力下降，机油无法驱动凸轮轴执行器工作的缘故。......
2023-08-30
相关推荐