当天空布满均匀的云层或多雾的天气时，散射辐射均匀分布于整个天空，也就是说，天空的散射辐射是各向同性的。可是一部分地方气象台仅检测并记录水平面上的太阳总辐射，即水平面上的直射辐射和散射辐射的总和。在使用这些数据时，就需要先把太阳总辐射分离成为直射辐射和散射辐射两部分。......
2023-06-23
黑体辐射基本定律
【摘要】：黑体的光谱辐射力与绝对温度T和波长λ的函数关系由如下普朗克定律表示为式中，σ称为黑体辐射常数，σ=5.669×10-8W/；C0称为黑体辐射系数，C0=5.669×10-8W/；下标b表示黑体；T为热力学温度；这一定律表明黑体的辐射力与绝对温度的四次方成比例，因此又称为辐射四次方定律。由图3-9可见黑体的光谱辐射力与波长λ的变化规律。
1.斯蒂芬-波尔兹曼（Stefan-Boltzmann）定律
在知道斯蒂芬-波尔兹曼定律之前，首先我们要了解辐射力这一概念，即单位时间内物体单位表面积向半球空间所有方向发射出去的全部波长的辐射能的总量，记为E，单位为W/m2。辐射力是从总体上表征了物体发射辐射能本领的大小。
黑体的辐射力和热力学温度（K）的关系由斯蒂芬-波尔兹曼定律所规定：
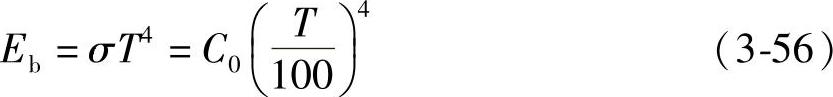
式中，σ称为黑体辐射常数，σ=5.669×10-8W/（m2·K4）；C0称为黑体辐射系数，C0=5.669×10-8W/（m2·K4）；下标b表示黑体；T为热力学温度（K）；
这一定律表明黑体的辐射力与绝对温度的四次方成比例，因此又称为辐射四次方定律。它是热辐射工程计算的基础。
2.普朗克（Planck）定律
普朗克定律建立了黑体辐射能与波长分布的规律，为了定量分析，需要引入光谱辐射力的概念。光谱辐射力是指单位时间内物体单位表面积向半球空间所有方向发射出去的包含λ的单位波长范围内的辐射能，记为Ebλ，单位为W/（m2·m）或者W/（m2·μm），需要注意的是单位的分母中的m或者μm表示的是单位波长的宽度。
黑体的光谱辐射力与绝对温度T和波长λ的函数关系由如下普朗克定律表示为
式中，Ebλ为黑体光谱辐射力[W/（m2·μm）]；λ为波长（μm）；T为黑体热力学温度（K）；e为自然对数的底数；C1为第一辐射常量，C1=3.7419×10-16；C2为第二辐射常量，C2=1.4388×10-2。由图3-9可见黑体的光谱辐射力与波长λ的变化规律。
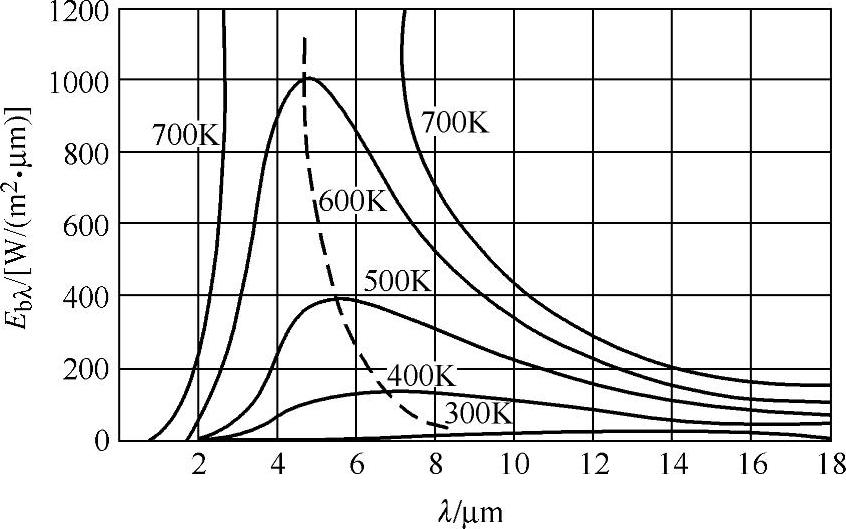
图3-9 普朗克定律图示
3.维恩（Wien）位移定律
将式（3-57）对λ求导并使其等于零便可得出：
λmT=208976×10-3m·K （3-58）
式中，λm为光谱辐射力最大处的波长。上式表达的波长λm与温度T成反比的规律即为维恩（Wien）位移定律。
4.兰贝特（Lambert）余弦定律
兰贝特余弦定律给出了黑体辐射能按空间方向的分布规律，在此引入立体角以及定向辐射强度的概念。
微元立体角以及立体角所在半球空间的球坐标如图3-10所示，微元立体角的定义如下式：
在球坐标系中，φ为经度角，θ为纬度角，由图3-10可求得
dAc=rdθrsinθdφ （3-60）
代入式（3-59）得到微元立体角为
dΩ=sinθdθdφ （3-61）
立体角的单位称为空间度，记作sr。
图3-10 微元立体角与半球空间几何参数的关系
定向辐射强度就是单位时间内单位可见辐射面积单位立体角的辐射能量。图3-11，实验测定表明：
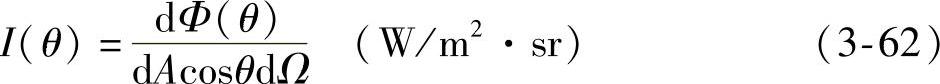
此处，I为常数，与θ无关。因此上式可写为：
式（3-63）表明黑体的定向辐射强度等于常量，与方向无关。这就是兰贝特余弦定律。需要注意的是定向辐射强度是以单位可见面积作为度量的依据，如果以实际辐射面积为度量依据，则就是式（3-62）所示的结果。因此黑体单位面积辐射出去的能量在空间不同方向的分布按纬度角θ的余弦规律变化，这是兰贝特余弦定律的另一种表达方式，即余弦定律。
图3-11 可见面积示意图
5.实际物体的辐射特性
黑体是所有物体当中吸收能力最大，同时发射能力也最大的理想化表面，这个特点使它很自然地成为了描述实际表面的吸收和发射能力大小的最佳基准。通常实际表面（固体或液体）的光谱辐射力比同温度的黑体小，而且表现不出像黑体那么有规律。一般对实际物体表面辐射进行一定程度的简化，再用辐射率和吸收率进行修正。引入辐射率是为了定量描述实际物体在发射辐射方面与黑体的差别，而引入吸收率是为了定量描述实际物体在吸收辐射方面与黑体的差别。
（1）发射率
实际物体的辐射力E总是小于同温度下黑体的辐射力Eb，因此引入发射率的概念，发射率用ε表示，即
因此，实际物体的辐射力可以表示为
E=εEb=εσT4 （3-65）这就是实际物体辐射换热计算的基础。发射率仅取决于物体自身，而与周围的环境条件无关。
（2）光谱发射率
实际物体的光谱辐射力小于同温度下黑体同一波长下的光谱辐射力，两者之比即为实际物体的光谱发射率定向辐射率，用ελ表示，即
显然光谱发射率与实际物体的发射率之间有如下关系：
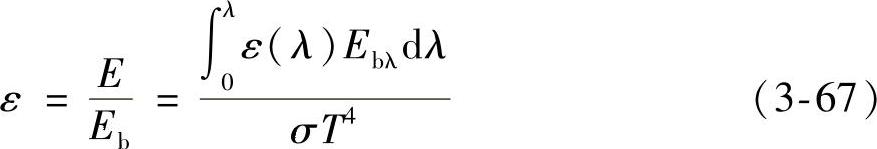
（3）定向辐射率
实际物体辐射按空间的分布，也不尽符合兰贝特余弦定律。为了说明不同方向上定向辐射强度的变化，在此给出定向辐射率的定义式
式中，Eθ、Ebθ分别是与辐射面法向成θ角的方向上实际物体与黑体的定向辐射强度。
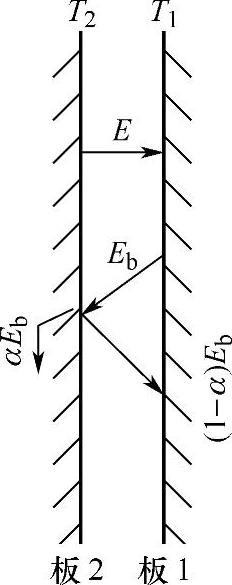
图3-12 说明基尔霍夫定律示意图
6.基尔霍夫（Kirchhoff）定律
基尔霍夫定律描述了物体发射辐射的能力和吸收辐射的能力之间的关系。此定律可从研究两个表面的辐射传热导出。假定图3-12中的两块平行平板间距很小，即从一块板发出的辐射全部落在另一块板上。若板1为黑体表面，其辐射力、吸收率和表面温度分别为Eb、αb（=1）和T1。板2为任意物体的表面，其辐射力、吸收率和表面温度分别为E、α和T2。现考虑板2的能量收支差额，板2辐射的能量E投射在板1上时被全部吸收。同时黑体表面1的辐射能量Eb只有αEb被板2吸收，其余部分（1-α）Eb被反射回板1，并被板1全部吸收，因此板2的能量收支差额就是两板间辐射传热的热流密度，即
q=E-αEb （3-69）
当T1=T2时，即处于平衡状态时，q=0。于是上式变为
推广到任意物体时，则可写出如下关系式：
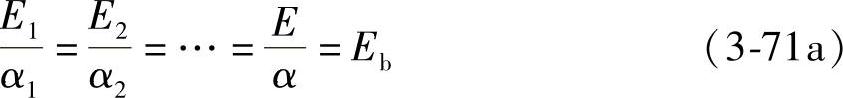
也可写成
式（3-71a）和式（3-71b）就是基尔霍夫定律的两种数学表达式。式（3-71a）可以表述为：在热平衡条件下，任何物体的自身辐射和它来自黑体辐射的吸收率的比值，恒等于同温度下黑体的辐射力。而式（3-71b）可表述为：热平衡时，任意物体对黑体投入辐射的吸收率等于同温度下该物体的发射率。
在此引入灰体的概念。如果物体的吸收率与波长无关，它就称为灰体，灰体也是一种理想物体。工业上的辐射传热计算一般都按灰体来处理。对于漫灰体，不论投入辐射是否来自黑体，也不论是否处于热平衡状态，其吸收比恒等于同温度下的发射率，这个结论可以给太阳能热利用系统中辐射传热的计算带来实质性的简化。
有关太阳能热发电站的文章
- 详细阅读
-
家电辐射防护实用指南详细阅读
研究表明，微波炉所产生的强电磁波严重超标可能会诱发疾病。3．电脑后部及两侧的电磁辐射强度不亚于屏幕的强度，要最好保持在120厘米以上。可是像收音机、随身听、手机等小的电器不适合放在床头，以免大脑受到电磁辐射。最后，如果长期处在电磁辐射源中，身体感到不适，应尽快找有关部门进行监测、测试，找出辐射源，避免长期受到伤害。......
2023-11-17
-
如何计算气体辐射和火焰辐射的传热量？详细阅读
在图中，1、2、3分别为气体辐射、预燃烧室内的火焰辐射和主燃烧室内的火焰辐射与辐射传热总量Qtotal之间的比率。此时努塞尔特数Nu定义为式中，为单位时间的平均传热量（散热量）；B为气缸内径；kg为气体热传导系数。由泰勒发表的气体相关温度Tg，a、黏性系数μg、热传导系数kg随当量比φ的关系如图8-15所示。......
2023-06-28
- 详细阅读
-
常用基本定律解析 - 优化标题详细阅读
如果要获得一定的磁通，为了减小磁通势，应尽量选用高磁导率的铁磁材料做铁芯，而且尽可能缩短磁路中不必要的气隙长度。铁磁材料有如下性质：能被磁体吸引。磁导率不是常数，每种铁磁材料都有一个最大值。铁磁材料有软磁材料、硬磁材料和矩磁材料三种。硅钢片、纯铁属软磁材料，常用来做电机的铁芯。钨钢、钴钢属硬磁材料，常用来做各式永久磁铁。......
2023-06-24
-
新世纪中国魔幻电影：想象辐射详细阅读
新世纪中国魔幻电影中有着丰富多彩的“第二世界”想象，主要方法是运用夸张、变形等陌生化手法，超越自然规律和现实逻辑，建立起一套丰富、完整的符号系统。具体而言，“第二世界”的构想主要由两部分组成，其一是空间，即影片发生的超现实环境；其二是种族，即影片中的神仙精怪等超自然族群。下文将从这两部分入手，对中国魔幻电影的“第二世界”想象，以及这种想象背后所折射的文化内蕴、权力关系等进行详细分析。......
2023-08-07
-
热辐射现象基本概念详解详细阅读
发射辐射能是各类物质的固有特性。显然，热辐射是电磁波传递能量的现象。通常把波长在0.1～100μm范围的电磁波称为热辐射。于是有α+ρ=1 当热辐射投到气体上时，由于气体对辐射能几乎没有反射能力，则可认为ρ=0。于是有α+τ=1 热辐射投射到物体表面后的反射现象有镜面反射和漫反射两种类型，区分反射类型取决于物体的表面粗糙度。......
2023-06-23
-
微波辐射合成苯甲酸乙酯详细阅读
实验二十八微波辐射合成苯甲酸乙酯（一）实验目的1.了解微波辐射的机理及微波反应的特点2.掌握微波反应的操作方法，并与常规方法进行对比（二）反应式（三）主要试剂及仪器苯甲酸2.5g，无水乙醇（分析纯）5mL，浓硫酸，苯（分析纯），碳酸钠，乙醚（分析纯），无水氯化钙改装的家用微波炉，25mL圆底烧瓶，分水器，回流冷凝管，蒸馏头，尾接管，直型冷凝器，锥形瓶，分液漏斗。......
2024-08-20
相关推荐