对流换热是指流体与固体壁面接触时彼此之间的传热。（二）对流换热系数对流换热系数α是表示流体换热能力大小的物理参数，它的值等于单位时间内流体和固体壁面温度相差1℃时，通过单位面积所传递的热量。由式Q=αS可知，影响对流换热的因素主要有三个：流体与壁面的温差、对流换热系数以及换热面积。这三个因素无论哪个增大，都可以提高对流换热的效果。......
2023-10-11
对流换热的经验公式
【摘要】：在太阳能利用系统的分析设计中，为了计算对流换热量，必须要知道牛顿冷却公式中的对流换热系数h。所以，一般我们将对流换热的实验数据整理成各无量纲数之间的关系式，以供在集合上与之相似的流动边界条件使用。因此，在确定实际问题中的对流换热系数时，必然会使用到如式和这样的准则公式。
在太阳能利用系统的分析设计中，为了计算对流换热量，必须要知道牛顿冷却公式中的对流换热系数h。但由于h受诸多因素的影响，对于大多数复杂的实际情况，很难用该分析的方法确定h。所以，一般我们将对流换热的实验数据整理成各无量纲数之间的关系式，以供在集合上与之相似的流动边界条件使用。此方法的基础是相似理论。
1.无量纲数
为了能正确应用对流换热的经验公式，先简要说明几个重要的无量纲数。
（1）努赛尔（Nusselt）数Nu
努赛尔数的定义式为
式中，h为对流换热系数[W/（m2·℃）]；L为传热面几何特征尺寸（m）；λ为流体的导热系数[W/（m·℃）]。
由定义式（3-9）可以看出，努赛尔数是一个反映对流换热强弱的无量纲数，表示为流体层的导热阻力与对流换热阻力的比例。实际情况中，由于水的导热系数比空气的导热系数要大出一个数量级以上，所以水相比空气在与固体壁面之间进行对流换热时的换热系数要大得多。
（2）雷诺（Reynolds）数Re
在前面章节中，我们已经给雷诺有过定义，其定义式为式（3-18）。
（3）普朗特（Prandtl）数Pr
普朗特数是有流体物性参数组成的一个无量纲参数群，表明温度边界层和流动边界层的关系，反映流体物理性质对对流传热过程的影响，它的表达式为
式中，Cp为流体的定压比热容[kJ/（kg·℃）]；μ为流体的动力粘度[kg/（m·s）]；λ为流体的导热系数[W/（m·℃）]。
Pr数也经常表示为
式中，a为热扩散系数（m2/s），a=λ/ρCp；ν为流体的运动粘度（m2/s），ν=μ/ρ。
式（3-21）表明Pr可以理解为流体的动量扩散能力与热量扩散能力之比。
（4）格拉晓夫（Grashof）数Gr
格拉晓夫数的表达式为
式中，g为重力加速度（m/s2）；β为流体的膨胀系数（1/K）；L为传热面几何特征尺寸（m）；ΔT为流体与壁面的温度之差（K）。
正如雷诺数决定了强迫对流的流动情况，格拉晓夫数反映的是自然对流流动强度对对流换热强度的影响，它可理解为流场中流体的浮升力与粘性力之比。
（5）瑞利（Rayleigh）数
瑞利数是在自然对流传热中与传热系数关联的无量纲参数，其表达式为
式中，g为重力加速度（m/s2）；β为流体的膨胀系数（1/K）；L为传热面几何特征尺寸（m）；ΔT为流体与壁面的温度之差（K）；a为热扩散系数（m2/s），a=λ/ρCp。
以上所述的Nu、Re、Pr、Gr、Ra等无量纲数也可称为“无量纲准则”或“准则数”。
对于强迫对流换热或者自然对流换热，我们可通过对边界层守恒方程的无量纲化，推导出对流换热系数与下述无量纲数之间的关系：
对于强迫对流换热，有
Nu=CRenPrm （3-24）
对于自然对流换热，有
Nu=C（GrPr）n （3-25）
以上两式中C、m、n都是由实验数据所确定的常数。
2.相似理论
在传热过程中，若两者传热现象相似，则由其中一个传热现象所得的实验数据就可应用于另一个传热现象。因此，我们就要清楚在什么条件下，两个传热现象才相似，即判断相似的条件是什么。
对于同类现象，如果单值性条件相似且同名已定准则数相等，则现象必定相似。其中单值性条件相似应包括几何条件相似、时间条件相似（非稳态传热）、物性相似以及边界条件相似。
相似理论表明，相似现象的同名准则数必定相等。若现象1和现象2相似，则两现象的各已定准则数和待定准则数应分别相等，这一相似性质将为实验结果的推广应用提供理论依据。
在太阳能利用系统中，吸热管或吸热板与工作流体的传热，透明盖板及储热箱外壁与周围环境的传热，空气加热器中的空气与吸热板之间的传热等，都是对流换热过程或者包含对流换热过程。因此，在确定实际问题中的对流换热系数时，必然会使用到如式（3-24）和（3-25）这样的准则公式。要使用这些准则公式，当然必须要满足单值性条件相似这个重要前提。
3.准则公式
接下来，介绍一些在太阳能热利用系统分析设计中常用的准则公式。
（1）管内层流换热
对于管壁温度沿流动方向为定值的管内层流换热，通过大量的实验结果提出了下列准则公式：
式中，D为管径；L为管长；μ、μs分别为按流体的平均温度和管壁温度所取定的流体的动力粘度；Nu、Re及Pr数中的流体物性都按流体的平均温度来取值，即
式中，Tf，i、Tf，o分别为流体进出口温度。
式（3-26）的实验验证范围为Pr=0.48～16700；μ/μs=0.0044～9.75；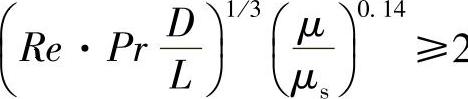
且管壁处于均匀温度。
在此范围下，可认为管长方向的绝大部分流动处于充分发展区，所以可近似分析得到Nu=3.66。
若沿流动方向管壁的热流密度是定值，则对于充分发展的管内层流换热可通过严格的分析得到Nu=4.36。
（2）管内湍流换热
对于管内湍流换热，学术上应用时间最长最普遍的关联式为
Nu=0.023Re0.8Prn （3-28）
加热流体时，n取0.4；冷却流体时，n取0.3。上式习惯上又称为Dittus-Boelter公式，该公式主要适用于流体与壁面温度温差为中等的场合。式中的流体物性也是采用流体的平均温度，与管内层流换热类似。
式（3-28）的实验验证范围为：Re=104～1.2×105，Pr=0.7～120，L/D≥60。
（3）非圆形管道内的强迫对流换热
以上讨论的是基于圆形管道的，在太阳能热利用系统中，会碰到一些异形的管道，如矩形，三角形等管道。因此，考虑采用水力直径DH作为特征尺度对圆管得出的湍流换热公式近似地予以利用，来计算Re和Nu。对于充分发展的异形管道的Nu数可见表3-1。
表3-1 充分发展的异形管道的Nu数
（4）流体横掠单管的强迫对流换热
在太阳能热利用系统中，经常会使用带有玻璃罩管的真空集热管，这就需要确定在有风速情况下空气横掠玻璃罩管的对流换热系数。对于Re>500的情况，可用下述准则公式：
Nu=0.46Re0.5+0.00128Nu （3-29）
式中，Re和Nu的特征尺度都按玻璃罩管的外径计算，速度取风速，物性参数取空气与玻璃罩管外表面在平均温度时的值。
（5）空气沿平板流动时的强迫对流换热
在一定风速下，空气流过太阳集热器的透明盖板时，都会发生强迫对流换热。在现有的太阳能热利用专著中，常采用下述近似公式：
hc=5.7+3.8v （3-30）
式中，v为风速（m/s）。但式（3-30）并未考虑平板的长宽比值及气流与平板间的攻角对换热的影响。
基于实验研究提出了下述通用性很强的准则公式，即
对式（3-31）的应用有专门的特征尺寸的规定，即
式中，A为平板面积；C为平板周长。式（3-31）适用于攻角范围25°～90°，ReL为2×104～9×104，最大误差为±10%。用式（3-30）计算会使h偏高。
（6）平行平板间的自然对流换热
太阳能热利用系统中，常常需要计算两块平行平板间的自然对流换热，如平板太阳集热器透明盖板与吸热板之间的空气夹层或者双层玻璃窗之间的空气夹层等的自然对流换热。
对于垂直放置的矩形空腔，有下述准则公式：
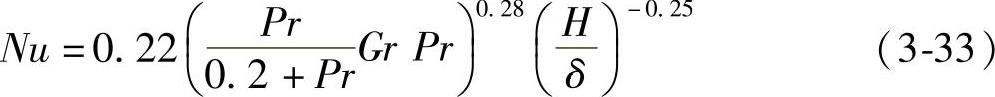
式中，H为夹层高度；δ为夹层间距。其适用范围为，2＜H/δ＜10，Pr＜105，GrPr＜1010。
对于H/δ很大的情况，则采用下述准则公式：
适用范围为10＜H/δ＜40，1＜Pr＜2×104，104＜GrPr＜107。
对于倾斜放置的矩形空腔，有下述准则公式：
适用范围为30°≤θ≤60°，12<H/δ<40，1.3×104＜GrPr＜106。
Nu=0.13（GrPr）0.285 （3-36）适用范围为0°≤θ≤15°，18＜H/δ＜40，2.2×104＜GrPr＜4×105。
在上述准则式中，特征尺寸都用空气夹层厚度δ，物性参数都按夹层冷热面的平均温度来取值。
（7）垂直壁的自然对流换热
对于垂直壁的自然对流换热，采用下述准则公式：
Nu=0.55（GrPr）1/4 （3-37）
适用范围为1700＜GrPr＜108。
Nu=0.13（GrPr） （3-38）
适用范围为GrPr＞108。
在以上两个准则公式中，特征尺寸为垂直壁的高度，物性参数按壁面温度和远离表面处空气温度的平均值选取。
有关太阳能热发电站的文章
- 详细阅读
- 详细阅读
-
物体表面间辐射换热优化详细阅读
同样，物体单位表面积的有效辐射称为有效辐射密度，用J表示。根据定义有J=e+ρG=εσT4+ρG 3.平板间的辐射换热设有两块靠的很近且平行放置的平板，不仅都是灰体，而且都是“朗伯表面”，如图3-13所示。根据发射率的定义及斯蒂芬-波尔兹曼定律，可知e=εeb=εσT4 投射辐射是指由外界投射在物体表面的辐射。......
2023-06-23
- 详细阅读
-
优化换热边界条件的文章标题详细阅读
采用有限元方法模拟温度场分布的关键是合理地给出换热边界条件。热分析采用第三类边界条件，主要是确定燃气的温度和燃烧室内壁面与燃气的对流换热系数。图3.10各转速对流换热系数不同转速下，缸内气体温度随偏心轴转角变化的曲线如图3.9所示。取气缸区域对应偏心轴转角的温度、对流换热的平均值作为换热边界条件。图3.11气缸内腔区域划分以发动机转速为17 000r/min为例，气缸内壁各区域所对应的对流换热边界条件如表3.3所示。......
2023-06-23
-
对流边界条件下平板和圆管壁换热量的比较详细阅读
根据牛顿冷却定律，可知流体与平板间的对流换热量为式中，Rc为对流热阻（℃/W）。如图3-7所示为两层圆管壁内较高温度的工作流体向较低温度的工作流体传热过程示意图及其热网络图。图3-7 通过两层管壁的传热速率上述总传热系数Ut是以圆管的内壁面积A1来定义的。......
2023-06-23
-
陶瓷干燥与烧成技术：两固体辐射换热计算详细阅读
（四）两固体间的辐射换热两个固体表面间的辐射换热，其换热量为高温物体向低温物体反复地反射和吸收的总结果，称净辐射换热量，用Qnet表示。两固体的形状、大小及相互位置关系千变万化，下面介绍两固体几种特殊位置关系的净辐射换热计算。若两平板的黑度分别为ε1、ε2，由于两平板面积相等，其净辐射换热量可用净辐射热流量qnet表示。......
2023-10-11
-
解锁元件热衰退故障：汽车维修经验与技巧集详细阅读
再从点火信号的源头查起，拔出曲轴位置传感器的插接器，起动发动机，测量曲轴位置传感器的端子上有无信号电压。如果没有信号电压，可以确定为曲轴位置传感器损坏，更换曲轴位置传感器，一般可以排除故障。连接故障诊断仪检测，故障信息为“曲轴位置传感器不可靠信号”。拆下曲轴位置传感器，用压缩空气吹凉，测量电阻为790Ω，处在680～1300Ω范围的下限。更换曲轴位置传感器后，故障排除。......
2023-08-30
相关推荐