罗睺寺位于五台山塔院寺的东侧。罗睺寺以罗睺命名，乃取罗睺刻苦自修，“不毁禁戒，诵读不懈”之意。罗睺寺为黄庙，殿内主要塑像颇具明显的喇嘛教的风格。罗睺寺殿阁一角罗睺寺最吸引人的是“开花现佛”。“开花现佛”的奇景已经于1984年修复，正式向游人开放。罗睺寺白塔五台山是佛教四大名山中唯一兼有汉藏两种风格寺院的佛教道场，集中体现了佛教艺术的魅力，堪称世界级佛教文化艺术的宝库。......
2023-12-06
什么是均质大气？它的作用及意义是什么？
【摘要】：在这里需要引入“均质大气”的概念。根据式（2-7）可知，在密度ρ不变的情况下，某一海拔高度的均质大气高度与当地的气压成正比。将气温t0=0℃，重力加速度g0=9.806m/s2，气压b0=1.01325×105Pa条件下的均质大气，定为“标准均质大气”。因此，光子同空气分子碰撞的机会以及大气的消光作用都完全可以用气压相应的均质大气来表征。有关均质大气的意义及使用这一概念的合理性即在于此。
当辐射通过某种介质时，必然会由于受到介质的吸收和散射而减弱。辐射受介质衰减的一般规律，早在1729年就被法国物理学家布格尔（Bouguer）用实验的方法确定下来，它的数学表达式为
式中，ϕ0为初始的辐射通量；ϕ为通过介质后的辐射通量；L为介质的相对厚度；τ为介质的透射比，当L=1时，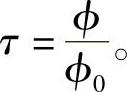
1760年德国物理学家朗伯（Lambert）又进一步进行了研究，指出辐射通量的相对变量dϕ/ϕ应与吸收介质层的厚度dL成正比，即
式中，ϕ0为初始的辐射通量；ϕ为通过介质后的辐射通量；L为介质的相对厚度；τ为介质的透射比，当L=1时，
1760年德国物理学家朗伯（Lambert）又进一步进行了研究，指出辐射通量的相对变量dϕ/ϕ应与吸收介质层的厚度dL成正比，即
将式（2-5）积分，当L=0时，ϕ=ϕ0，整理后可得
式中，μ为线性衰减系数。
将式（2-5）积分，当L=0时，ϕ=ϕ0，整理后可得
式（2-6）实际上就是式（2-4），因此通常称为布格尔-朗伯定律。
布格尔-朗伯定律是在均匀介质条件下得到的。这意味着，在气体介质中，各处的温度、湿度、气压等项参数都应是相同的。而这样的条件在实际大气中是无法满足的。为了说明布格尔-朗伯定律对地球大气的适用性，必须将实际上物理不均匀的大气看作是均质大气。
在这里需要引入“均质大气”的概念。所谓均质大气是有条件的大气，即大气中空气的密度到处都相同，成分也与实际大气无异，而当地的气压也与实际大气相同。均质大气与实际大气的区别仅在于，均质大气的高度是一个完全确定的数值，并满足下式：
式（2-6）实际上就是式（2-4），因此通常称为布格尔-朗伯定律。
布格尔-朗伯定律是在均匀介质条件下得到的。这意味着，在气体介质中，各处的温度、湿度、气压等项参数都应是相同的。而这样的条件在实际大气中是无法满足的。为了说明布格尔-朗伯定律对地球大气的适用性，必须将实际上物理不均匀的大气看作是均质大气。
在这里需要引入“均质大气”的概念。所谓均质大气是有条件的大气，即大气中空气的密度到处都相同，成分也与实际大气无异，而当地的气压也与实际大气相同。均质大气与实际大气的区别仅在于，均质大气的高度是一个完全确定的数值，并满足下式：
式中，H为大气离地面的高度（m）；b为当地的气压（N/m2）；ρ为大气中空气的密度（kg/m3）；g为重力加速度（m/s2）。
根据式（2-7）可知，在密度ρ不变的情况下，某一海拔高度的均质大气高度与当地的气压成正比。将气温t0=0℃，重力加速度g0=9.806m/s2（即纬度45°的海平面处），气压b0=1.01325×105Pa（1.01325×105N/m2）条件下的均质大气，定为“标准均质大气”。在上述条件下，空气密度ρ0=1.2923kg/m3。将各有关值代入式（2-7），求出H0=8km。
根据均质大气的定义可知，这种大气在单位面积上的垂直气柱内所包含的空气质量与实际大气完全一样，因此气体分子的数目也完全相同。实际上，在1cm2的面积上高度为H0的垂直气柱内共计有2.18×1025个空气分子，在这一方面与实际大气并无差别。因此，光子同空气分子碰撞的机会以及大气的消光作用都完全可以用气压相应的均质大气来表征。这种以有条件的均质大气来替换实际大气的方法，对于各种日射的计算结果并不会带来任何偏离，相反可使得各种计算大大简化。有关均质大气的意义及使用这一概念的合理性即在于此。
式中，H为大气离地面的高度（m）；b为当地的气压（N/m2）；ρ为大气中空气的密度（kg/m3）；g为重力加速度（m/s2）。
根据式（2-7）可知，在密度ρ不变的情况下，某一海拔高度的均质大气高度与当地的气压成正比。将气温t0=0℃，重力加速度g0=9.806m/s2（即纬度45°的海平面处），气压b0=1.01325×105Pa（1.01325×105N/m2）条件下的均质大气，定为“标准均质大气”。在上述条件下，空气密度ρ0=1.2923kg/m3。将各有关值代入式（2-7），求出H0=8km。
根据均质大气的定义可知，这种大气在单位面积上的垂直气柱内所包含的空气质量与实际大气完全一样，因此气体分子的数目也完全相同。实际上，在1cm2的面积上高度为H0的垂直气柱内共计有2.18×1025个空气分子，在这一方面与实际大气并无差别。因此，光子同空气分子碰撞的机会以及大气的消光作用都完全可以用气压相应的均质大气来表征。这种以有条件的均质大气来替换实际大气的方法，对于各种日射的计算结果并不会带来任何偏离，相反可使得各种计算大大简化。有关均质大气的意义及使用这一概念的合理性即在于此。
有关太阳能热发电站的文章
- 详细阅读
-
妻权是什么,妻权是什么意思详细阅读
事前知晓妻子与他人通奸，但不表示反对的，基于知情故纵，丈夫丧失因妻犯奸的离婚请求权。夫之于妻如有诬奸告官之事实，则行同义绝，并非轻微口角及无关重要之詈责可比，应认为有重大侮辱，准其妻请求离异。[69]该第1012号判例与上述第717号判例，均认为丈夫诬告妻子与他人通奸是得以请求离婚的“重大侮辱”情形，妻子可以据此请求离婚。因此，丈夫诬奸告官，妻子获得离婚请求权。......
2023-07-03
-
张亚子是文昌祖庭，究竟是什么神？详细阅读
张亚子究竟是什么神普天而言的尊神文昌帝，专司人间科名官位禄籍，原来家就藏在苍柏翠林深山间，倒是让我颇感意外。民间流传的张亚子是什么神的说法五花八门，我主要说其中三种。一种是说张亚子是蛇神的化身。还有一种说法是张亚子是个雷神。张亚子以孝悌为美名，后得道成神。也有人认为张亚子就是蜀人张育。后张育祠与同山之梓潼神亚子祠合称，张育即传称张亚子。......
2024-09-06
-
打油诗是什么诗，是在打油的路上做的诗吗？详细阅读
第104问：“打油诗”是什么诗，是在打油的路上做的诗吗我们今天通常将那些内容和词句通俗诙谐、不拘于平仄韵律，所谓“不能登大雅之堂”的旧体诗称作“打油诗”，这是为什么呢？原来在中唐时期，有一位名叫张打油的人，他就爱作这样的诗。因此，后人便将此类诗作取其名字定义为“打油诗”。有位师爷上禀道：“大人不用查了，作这类诗的不会是别人，一定是张打油。”......
2023-08-08
-
电磁炉的工作原理是什么？详细阅读
图1-20所示为电磁炉工作原理等效电路。图1-20 电磁炉工作原理等效电路1）从电路中可以看出，系统检测是电磁炉用来检测锅底温度和元器件温度的，当温度达到设定值或极限值时，系统将作出相应的反应。功率控制用来控制电磁炉IGBT栅极脉冲的幅度和宽度，以此来控制IGBT是导通还是截止，以及导通和截止时间的长短，以达到控制电磁炉功率大小的目的。显示电路是用来显示电磁炉各项技术指标的，以方便消费者操作。......
2023-06-20
-
科技论文写作的目的是什么详细阅读
近年来，中国学者发表论文的数量逐年上升。为什么我们要写科技论文呢？但这绝不是发表科技论文的真正目的，而是因为论文的发表以及论文的质量证明了作者研究工作的成果和质量。撰写科技论文的过程本身是科学研究的最基本的机制之一；发表科技论文，向同行报告最新成果，是进行学术交流的重要途径。......
2023-07-08
-
塑料的主要成分是什么？详细阅读
塑料是以合成树脂为主要成分，并根据不同需要添加不同添加剂所组成的。塑料按其成分不同，可分为简单组分和多组分的塑料。填充剂的用量通常为塑料组成的40％以下。塑料的老化现象，就是由增塑剂中的某些挥发物质逐渐从塑料制品中逸出而产生的，因此，在塑料中应尽量减少增塑剂含量。因此，在大多数塑料中都要添加稳定剂，用以减缓和阻止塑料在加工和使用过程中的分解变质。......
2023-06-26
-
另类整形风潮，隐藏的危害是什么？详细阅读
另类整形得不偿失一些比传统整形更为另类的整形项目在年轻人中蔚然成风。但是，不管什么样的整形手术，都会有伤口感染、愈合不佳、麻醉药过敏、影响身体正常功能等危险。那么，另类整形到底有哪些，又可能导致哪些严重的后果呢？鼻腔内部细菌本来就较多，术后更容易引起感染发炎，甚至病毒感染，不卫生的操作还会造成交叉感染。容易造成牙釉质损坏，引起牙质过敏，缩短牙齿的寿命。这项整形手术经常由于消毒不严而引发病毒感染。......
2023-12-04
相关推荐