【摘要】:粒子群优化算法,是Eberhart和Kennedy[118]提出的一种基于群体智能的优化算法,它是受鸟群和鱼群群体运动的行为方式启发而得到的。这些算法从不同方面对粒子群优化算法进行了改进,不同程度地提高了优化算法的收敛速度和精度,但是效果不是很理想。高鹰等人把混沌思想引入粒子群优化算法中,提出了混沌粒子群优化算法[127-129],取得了良好的效果。因此,本书拟采用混沌粒子群优化算法对风—光—抽蓄复合发电系统进行优化配置。
粒子群优化(Particle Swarm Optimization,PSO)算法,是Eberhart和Kennedy[118]提出的一种基于群体智能的优化算法,它是受鸟群和鱼群群体运动的行为方式启发而得到的。该算法的基本思想来源于对鸟群简化社会模型的研究及行为模拟,其中的每个个体充分利用群体的与自身的智能,不断地调整学习,最终得到满意解。在PSO算法中,每个备选解是搜索空间中的一个粒子,每个粒子根据它自身的经验和粒子群的最佳经验,在问题空间中向更好的位置飞行,如此循环搜索直到发现最优解。
PSO算法作为一种新的进化算法,可用于解决大量非线性、不可微和多峰值的复杂优化问题,并已广泛应用于科学和工程领域。与基于达尔文“适者生存,优胜劣汰”的进化思想不同,PSO算法是通过个体之间的协作来寻找最优解,每个粒子都被赋予一个随机速度并在整个问题空间中流动,粒子具有记忆功能,粒子进化不是通过遗传算子而是通过粒子之间的合作和竞争来实现的。它利用了生物群体中信息共享会产生进化优势的思想,其运算简单,易于实现。
PSO算法的标准形式见式(4-1)。
式中 xk——第m个粒子在第k次迭代中的位置;
式中 xk——第m个粒子在第k次迭代中的位置;
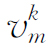 ——第m个粒子在第k次迭代中的速度;
——第m个粒子在第k次迭代中的速度;
pbestm——第m个粒子的个体最优解;
gbest——全局最优解;
r1、r2——[0,1]之间的随机数;
c1、c2——学习因子,用于控制收敛的速度;
ω——惯性系数。
整个算法的执行步骤如下:
(1)初始化粒子的位置及速度,并计算每个粒子的适应值,求出全局最优个体,并令当前个体为个体最优解。
(2)按照公式(41)计算本次迭代粒子移动速度。
(3)按照公式(4-2)计算本次迭代粒子位置。
(4)计算每个粒子的适应值:如果粒子的适应值优于其个体极值,则对其个体极值进行更新;如果粒子的适应值优于全局最优值,则进一步更新全局最优值。
(5)如果迭代次数达到了事先预定的最大迭代数或者满足了其他迭代中止条件(如已找到理论最优值),则停止迭代。否则转第(2)步。
算法中一些参数的典型值如下:
(1)粒子个数:一般取20~50,粒子太少会使其在解空间内的分布过于分散,容易陷入局部最优解;如果粒子数太多将会显著降低运算速度,使收敛变慢。
(2)最大迭代次数:与运算时间直接相关,可根据不同实例的收敛速度改变取值,一般100~500次迭代就足以找到最优解,如果经过很多次迭代仍不收敛,则可能是其他参数设置不当。
(3)粒子运动速度限值:粒子的运动速度每次迭代都会更新,但必须设立上下限,否则可能会导致某些粒子在一定的区域内反复振荡。但这个上下限也不能过小,否则会阻碍粒子收敛速度,或陷入局部最优解。具体的取值范围可以根据多次实际摸索确定。
(4)惯性系数:惯性系统增大将加强算法全局搜索能力,反之则增强局部搜索能力。为了改善PSO算法的性能,在迭代初期进行大范围的搜索,而在迭代末期算法趋于收敛情况下进行小范围的搜索。很多文献采用逐步递减惯性系统的方法。
(5)学习因子:通常设定学习因子c1=c2=2。
但Kennedy提出的粒子群存在不足,例如进化后期存在搜索速度变慢,过早收敛,易陷入局部最优解等。因此,国内外很多学者提出了改进的粒子群优化算法,例如Shi Y提出的带惯性因子的粒子群优化算法[119]和模糊自适应粒子群优化算法[120];借鉴遗传算法的思想,Angeline P.J.提出了杂交粒子群优化算法[121];Lovbjerg M提出了具有繁殖和子群的粒子群优化算法[122];Higasshi N提出了具有高斯变异的粒子群优化算法[123];为控制粒子的飞行速度,Clerc M提出的带约束因子的粒子群优化算法[124];为了使粒子群优化算法更易跳出局部极值点,Van提出了协同粒子群优化算法[125,126]。这些算法从不同方面对粒子群优化算法进行了改进,不同程度地提高了优化算法的收敛速度和精度,但是效果不是很理想。高鹰等人把混沌思想引入粒子群优化算法中,提出了混沌粒子群优化算法(Chaos Particle Swarm Optimization,CPSO)[127-129],取得了良好的效果。因此,本书拟采用混沌粒子群优化算法对风—光—抽蓄复合发电系统进行优化配置。
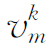 ——第m个粒子在第k次迭代中的速度;
——第m个粒子在第k次迭代中的速度;
pbestm——第m个粒子的个体最优解;
gbest——全局最优解;
r1、r2——[0,1]之间的随机数;
c1、c2——学习因子,用于控制收敛的速度;
ω——惯性系数。
整个算法的执行步骤如下:
(1)初始化粒子的位置及速度,并计算每个粒子的适应值,求出全局最优个体,并令当前个体为个体最优解。
(2)按照公式(41)计算本次迭代粒子移动速度。
(3)按照公式(4-2)计算本次迭代粒子位置。
(4)计算每个粒子的适应值:如果粒子的适应值优于其个体极值,则对其个体极值进行更新;如果粒子的适应值优于全局最优值,则进一步更新全局最优值。
(5)如果迭代次数达到了事先预定的最大迭代数或者满足了其他迭代中止条件(如已找到理论最优值),则停止迭代。否则转第(2)步。
算法中一些参数的典型值如下:
(1)粒子个数:一般取20~50,粒子太少会使其在解空间内的分布过于分散,容易陷入局部最优解;如果粒子数太多将会显著降低运算速度,使收敛变慢。
(2)最大迭代次数:与运算时间直接相关,可根据不同实例的收敛速度改变取值,一般100~500次迭代就足以找到最优解,如果经过很多次迭代仍不收敛,则可能是其他参数设置不当。
(3)粒子运动速度限值:粒子的运动速度每次迭代都会更新,但必须设立上下限,否则可能会导致某些粒子在一定的区域内反复振荡。但这个上下限也不能过小,否则会阻碍粒子收敛速度,或陷入局部最优解。具体的取值范围可以根据多次实际摸索确定。
(4)惯性系数:惯性系统增大将加强算法全局搜索能力,反之则增强局部搜索能力。为了改善PSO算法的性能,在迭代初期进行大范围的搜索,而在迭代末期算法趋于收敛情况下进行小范围的搜索。很多文献采用逐步递减惯性系统的方法。
(5)学习因子:通常设定学习因子c1=c2=2。
但Kennedy提出的粒子群存在不足,例如进化后期存在搜索速度变慢,过早收敛,易陷入局部最优解等。因此,国内外很多学者提出了改进的粒子群优化算法,例如Shi Y提出的带惯性因子的粒子群优化算法[119]和模糊自适应粒子群优化算法[120];借鉴遗传算法的思想,Angeline P.J.提出了杂交粒子群优化算法[121];Lovbjerg M提出了具有繁殖和子群的粒子群优化算法[122];Higasshi N提出了具有高斯变异的粒子群优化算法[123];为控制粒子的飞行速度,Clerc M提出的带约束因子的粒子群优化算法[124];为了使粒子群优化算法更易跳出局部极值点,Van提出了协同粒子群优化算法[125,126]。这些算法从不同方面对粒子群优化算法进行了改进,不同程度地提高了优化算法的收敛速度和精度,但是效果不是很理想。高鹰等人把混沌思想引入粒子群优化算法中,提出了混沌粒子群优化算法(Chaos Particle Swarm Optimization,CPSO)[127-129],取得了良好的效果。因此,本书拟采用混沌粒子群优化算法对风—光—抽蓄复合发电系统进行优化配置。

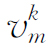 ——第m个粒子在第k次迭代中的速度;
——第m个粒子在第k次迭代中的速度;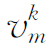 ——第m个粒子在第k次迭代中的速度;
——第m个粒子在第k次迭代中的速度;





相关推荐