金属表面氧化膜的生长特性

2025-09-29 理论教育版权反馈

【摘要】：在这种情况下，表面氧化膜的生长取决于电子能否移入氧化膜中。图1-10在室温下，Cu、Fe、Al、Ag的氧化膜厚度随时间的变化2.薄氧化膜的生长规律按反对数规律，氧化膜停止生长的原因是膜厚的增加导致膜中电场强度的减小，致使离子的移动发生困难。此时，离子电流的强度与电场强度之间已不再符合指数关系，也就是说在超过室温的较高温度下，氧化膜的生长规律已不再适用。

金属氧化后生成氧化膜，因此氧化膜的厚度就可以代表金属腐蚀的量，根据氧化膜的厚度随时间的变化，就可以知道金属的腐蚀速度以及氧化膜对腐蚀速度的影响。

金属氧化的速度主要取决于金属和氧在氧化膜中的扩散速度，扩散速度则与氧化膜的缺陷形式有关。不同金属，氧化膜的生长规律不同；同一金属在不同温度下氧化时，也会遵循不同的规律；即使同一金属在同一温度下，随着氧化时间的延长和氧化膜厚度的增加，膜生长的动力学规律也会发生变化。通常在低温和氧化膜较薄时，膜的生长规律符合对数关系、反对数关系或渐近线关系；在氧化膜较厚时，一般按抛物线关系或直线关系生长。

1.极薄氧化膜的生长规律

金属氧化时，首先是氧分子在金属表面上发生物理吸附，由于氧与电子的亲和力很大，吸附的氧原子形成O^2-离子，致使金属表面带正电，于是在氧和金属界面上形成一个双电层。由于双电层的形成，产生了约10⁷V/cm的极强电场，在此电场的作用下，能把金属离子从金属表面晶格中拉出，也能把氧离子吸入到金属晶格中。由于这样的物质移动，形成了三维的氧化物晶核。晶核先横向扩展，直至把整个表面覆盖后，再向厚度方向生长。由于这层氧化膜的存在，反应物必须通过膜内扩散才能到达反应地点。反应物在膜内移动的推动力就是膜中扩散粒子的浓度梯度，存在于膜上的电位梯度即电场强度。

在只有1～10nm极薄氧化膜的情况下，温度较低时离子的扩散离子移动的推动力主要是电位梯度。如果把金属离子脱离晶格而移向氧化膜所需要的能量记作W，将电子移向氧化物导带所需的能量记作Φ，按W<Φ和W>Φ两种情况来进行讨论。

（1）W<Φ的情况　当W<Φ时，金属离子在强电场的作用下移入氧化膜，此时电子的移动较困难，所以电子的移动成了反应速度的控制步骤。在这种情况下，表面氧化膜的生长取决于电子能否移入氧化膜中。如果电子脱出功Φ大于1eV，在常温下就不能发生热电子发射现象，因此就不能进行氧化。但是在极薄氧化膜的情况下，存在着量子力学的隧道效应，使电子能够移入氧化膜中，因此发生了膜的生长。隧道效应随膜厚的增加呈指数函数减小，当膜厚达到4nm时电子就不能通过了。因此膜的生长速度也是随着膜的厚度呈指数函数减小，直至最后停止。在这种情况下，膜的生长速度与电子因隧道效应而通过膜的几率成正比，如果以Y表示膜厚，其反应速度可表示为

式中，K为常数；h为普朗克常数，即6.626×10^-34J·s；m_e为电子质量，即9.109×10^-31kg；Φ为势垒高度。

将式（1-13）积分，得

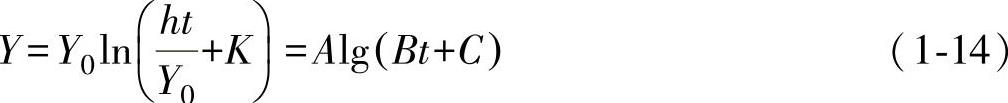
此时，Y和lgt呈线性关系，这就是对数规律，如Cu氧化为Cu₂O、200℃以下Ni的氧化、225℃以下Zn的氧化等都属于这种情况。

（2）W>Φ的情况　当氧化膜再厚一些时，由于氧化膜对离子移动阻力的增加要大于对电子移动阻力的增加，因此当膜达到一定厚度时就变为W>Φ，离子的移动成了决定反应速度的控制步骤。所以即使是在通常认为离子不能移动、氧化不能发生的特定温度下，由于极薄膜上吸附氧后产生的强电场的影响，离子的移动还是可能发生的，也就是说氧化膜还是能够继续生长。在约10⁷V/cm的强电场下，膜内的电位梯度为E时，离子电流i_ion的大小按下式指数函数关系变化：

式中，K为常数；Z为移动离子的电荷数，即离子价数；a为势垒的谷间距，可以在位能曲线上求得；e为电子电荷，即1.602×10^-19C；k为玻尔兹曼常数，即1.381×10^-23J/K。

由于氧化速度与i_ion成正比，E=V/Y，因此膜厚的生长速度可由下式表示：

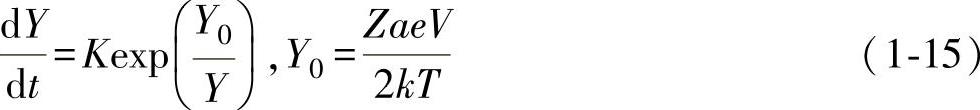
即在电场的影响下，膜的增厚速度按指数关系逐渐减慢，当膜达到一定厚度时，金属离子的扩散停止了，膜的生长也就完全停止。将式（1-15）积分可得下式：

1/Y与lgt成正比，这就是反对数规律。Cu、Fe、Al、Ag等在室温或稍高于室温时的氧化就属于这种情况，如图1-10所示，在2～3h内，膜迅速增加到一定厚度，随后氧化速度显著变小，以至几乎完全停止。

图1-10　在室温下，Cu、Fe、Al、Ag的氧化膜厚度随时间的变化

2.薄氧化膜的生长规律

按反对数规律，氧化膜停止生长的原因是膜厚的增加导致膜中电场强度的减小，致使离子的移动发生困难。但是如果升高温度，给予了离子移动所需的能量，则氧化反应又可以继续进行，氧化膜又会不断增厚。这时的电场作用力已经不足以推动离子移动，但给予了离子移动的方向。此时，离子电流的强度与电场强度之间已不再符合指数关系，也就是说在超过室温的较高温度下，氧化膜的生长规律已不再适用。这种情况出现在膜厚为10～300nm范围内的薄膜上，其生长规律因缺陷氧化物类型的不同而有所差异。

（1）金属过剩型氧化物　金属过剩型氧化物膜生长的控制步骤是间隙阳离子在膜内的移动，所以反应速度与晶格内间隙阳离子电流i_ion的大小成正比，而i_ion又与膜内的电场强度E和间隙阳离子的浓度n_ion成正比。在实际的氧化膜中，由于反应的迟缓以及离子移动的缓慢，使得金属-氧化物和氧化物-氧气的界面之间总是存在着表面电荷，如图1-10a所示。当表面膜较薄时，可以忽略膜内的空间电荷，因此可得到一个简化的双电层模型，如图1-11b所示。

图1-11　界面双电层

a）实际氧化膜中的界面双电层 b）简化的双电层模型

简化的双电层模型是一个电容器型的双电层，膜内的电位梯度是恒定的，膜内电场强度随膜厚的增加而按比例减小。根据这一假定，E与Y^-1成正比，膜厚的Y的生长可表示为

积分后得抛物线规律：

Y²=Kt

式中，K为常数，它与厚膜理论求得的速度常数具有完全不同的意义。

实验已证明，400℃时Al的氧化、350～400℃时Zn的氧化都符合这种规律。

（2）金属不足型氧化物　具有金属不足型氧化物的金属发生氧化时，离子在膜中的浓度梯度和电场强度作用下的移动过程是氧化反应进行的控制步骤。与金属过剩型氧化物中的间隙阳离子是在金属-氧化物界面上的金属进入氧化物内而形成的情况不同，金属不足型氧化物的阳离子空位，则是在氧化物-氧气界面上，由氧化物与吸附氧离子O^-之间反应而生成的。所以阳离子空位浓度n_□与表面吸附的氧离子浓度成正比

由于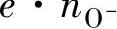等于氧化物-氧气界面的表面电荷密度，所以电场强度E与之间的

关系为

式中，ε为氧化物的介电常数。由于E随膜厚的增加而减小，所以膜中的缺陷浓度n□也应随膜厚Y的增加而成比例地减小，即E∝Y^-1，n_□∝Y^-1，所以(https://www.chuimin.cn)

积分后，得到立方规律：

Y³=kt

实验中可观察到，350℃时Ta的氧化、216℃时Ti的氧化、400℃或475℃时Ni的氧化等都符合立方规律。

3.厚氧化膜的生长规律

氧化膜厚度在100nm以上时称为厚氧化膜。在温度升高时，金属离子向氧化膜中移动的趋势将增加，由于热电子发射，电子的移动也变得容易了。金属离子和电子在氧化膜中移动的结果，使晶格缺陷、准自由电子和正孔等在膜内得以均匀分布，导致氧化膜内各处都能保持电中性。此时膜层较厚，所以双电层的影响减弱。在这种情况下，粒子移动的推动力不再以电场的影响为主，而主要考虑浓度梯度。因此，氧化膜的生长规律取决于下列三个过程中以何者为控制步骤：

1）金属-氧化物的界面反应，反应阻力用W_R1表示。

2）由于氧化膜中的浓度梯度而引起的离子扩散，扩散阻力用W_D表示。

3）氧化物-氧气的界面反应，反应阻力用W_R2表示。

氧化反应速度的一般式可以表示为

式中，ΔC为膜中氧气或金属的浓度梯度；W_R1、W_R2为相界面的反应阻力；W_D为氧化膜内的扩散阻力。

温度对反应阻力W_R的影响不大，所以即使在高温时也不能忽略。但温度对W_D的影响很大，低温时扩散阻力很大，但随着温度的升高而迅速减小。所以在一定的厚度范围内，由于温度的不同，氧化反应的控制步骤既可能是扩散过程，也可能是界面反应，因而显现出不同的生长规律。

（1）抛物线规律　当膜内扩散阻力很大，相对来说相界面的反应阻力可以忽略时，由于扩散阻力与氧化膜厚度成正比，即W_D=aY，所以式（1-16）可以简化为

在此，k/a为扩散系数。在通常情况下，扩散离子在膜两边的浓度，一边为饱和值，另一边接近于零，所以浓度梯度大致认为是一个恒定值，因此取kΔC/a=K，于是式（1-17）变换为

将式（1-18）积分，若当t=0时，Y=0，则得到：

Y²=2Kt

所以氧化膜的增长符合抛物线规律。Fe、Cu等大多数金属在生成厚而致密氧化膜的高温氧化过程中都符合抛物线规律。换句话说，当抛物线规律成立时，生成厚而致密的氧化膜，并且膜中的离子扩散是反应速度的控制因素。

（2）混合抛物线规律　当相界面的反应阻力W_R不能忽略，并且不随时间而变化，在一定温度下有一定值时，即

WR₁+W_R2=b，W_D=aY （1-19）

将式（1-19）代入式（1-16），可得

取kΔC=K，将式（1-20）积分，得

aY²+2bY=2Kt （1-21）

将式（1-21）变形，得

从式（1-22）中可以得出Y与t/Y呈直线关系。Fe、Cu、Ni等在低氧分压环境中氧化时，如Fe在水蒸气中的氧化，就属于这种情况。

（3）直线规律　若氧化膜内离子的扩散非常迅速，而界面反应速度却较慢时，界面反应就成为氧化反应速度的控制因素。此时，离子的扩散阻力忽略不计，即假设W_D=0，则式（1-20）可改写为

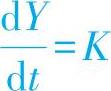
将上式积分，并假设t=0时，Y=0，则

Y=Kt

即界面反应控制的高温氧化反应中，膜的生长速度与原有的膜厚度无关，膜厚度随时间成正比地增加，称之为直线规律。

例如，900～1000℃下在CO-CO₂气氛中Fe氧化为FeO的反应和Cu在1000℃的氧化反应等都符合直线规律。但是，如果Fe的氧化是在900℃以下进行时，由于氧化膜内的扩散阻力W_D的增大，反应应符合抛物线规律。

上面介绍了金属氧化时的各种生长规律，任何一种金属放在室温下的大气中，最初均迅速地被氧化，在完全没有氧化物的金属表面上最初的氧化总是符合直线规律，但不久氧化速度急剧减慢。在电子移动成为速度控制步骤时符合对数规律；在离子移动成为速度控制步骤时符合反对数规律，所以在室温下生成的氧化膜厚度都不会超过一定的限度，一般为2～3nm的保护性氧化膜。大多数金属在室温或稍高于室温的情况下都具有这种性质。但在100℃以上的高温时，各种金属就显现出不同的规律。温度在100～500℃之间时，基本上都符合抛物线规律，但也有少数金属符合立方规律。当温度在1000℃或1000℃以上时，有的金属符合抛物线规律，也有的金属符合直线规律。在氧化反应过程中，膜内物质一般来说移动总是比较慢的，所以按抛物线规律进行氧化的情况最为普遍。表1-4列出了各类金属氧化膜厚度与时间关系的速度方程式。

表1-4　各类金属氧化膜厚度与时间关系的速度方程式

金属表面氧化膜的生长特性

相关推荐