1986年数学家Y.Meyer 构造出第一个真正的小波基，并与S.Mallat 合作建立了构造小波基的方法及其多尺度分析之后，小波分析才开始蓬勃发展起来，比利时女数学家I.Daubechies 撰写的《小波十讲》 对小波的普及起了重要的推动作用。因此，小波变换在信号分析和图像处理领域获得了广泛的应用。通过调整尺度因子，可以得到具有不同时频宽度的小波以匹配原始信号的不同位置，达到对信号的局部分析的目的。......
2023-11-19
小波数字信号处理技术
【摘要】：图10-7 一维小波分解简图一维小波的信号除噪是小波分析的重要应用之一。图10-9 一维信号小波除噪Simulink模型对信号除噪的目的就是抑制信号中的噪声部分，从而在信号中恢复有用信号。图10-11 二维图像信号小波除噪图10-11 二维图像信号小波除噪
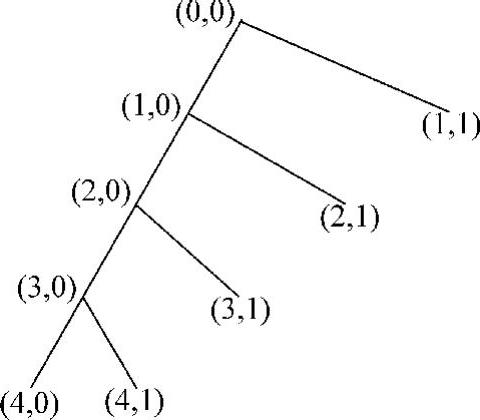
图10-7 一维小波分解简图
一维小波的信号除噪是小波分析的重要应用之一。在某些情况下，有用信号表现为低频信号或是一些比较平稳的信号，而噪声则表现为高频信号，所以除噪过程可按如下方法进行处理：首先对信号进行小波分解，采用db4进行4层分解如图10-7所示，则噪声部分通常包含在（1，1）、（2，1）、（3，1）和（4，1）中，因而可以以门限阈值等形式对小波系数进行处理，然后对信号进行重构，从而达到消除噪声的目的。图10-8是一维信号s按照db2小波6层分解的结果。一维信号小波除噪Simulink模型如图10-9所示。
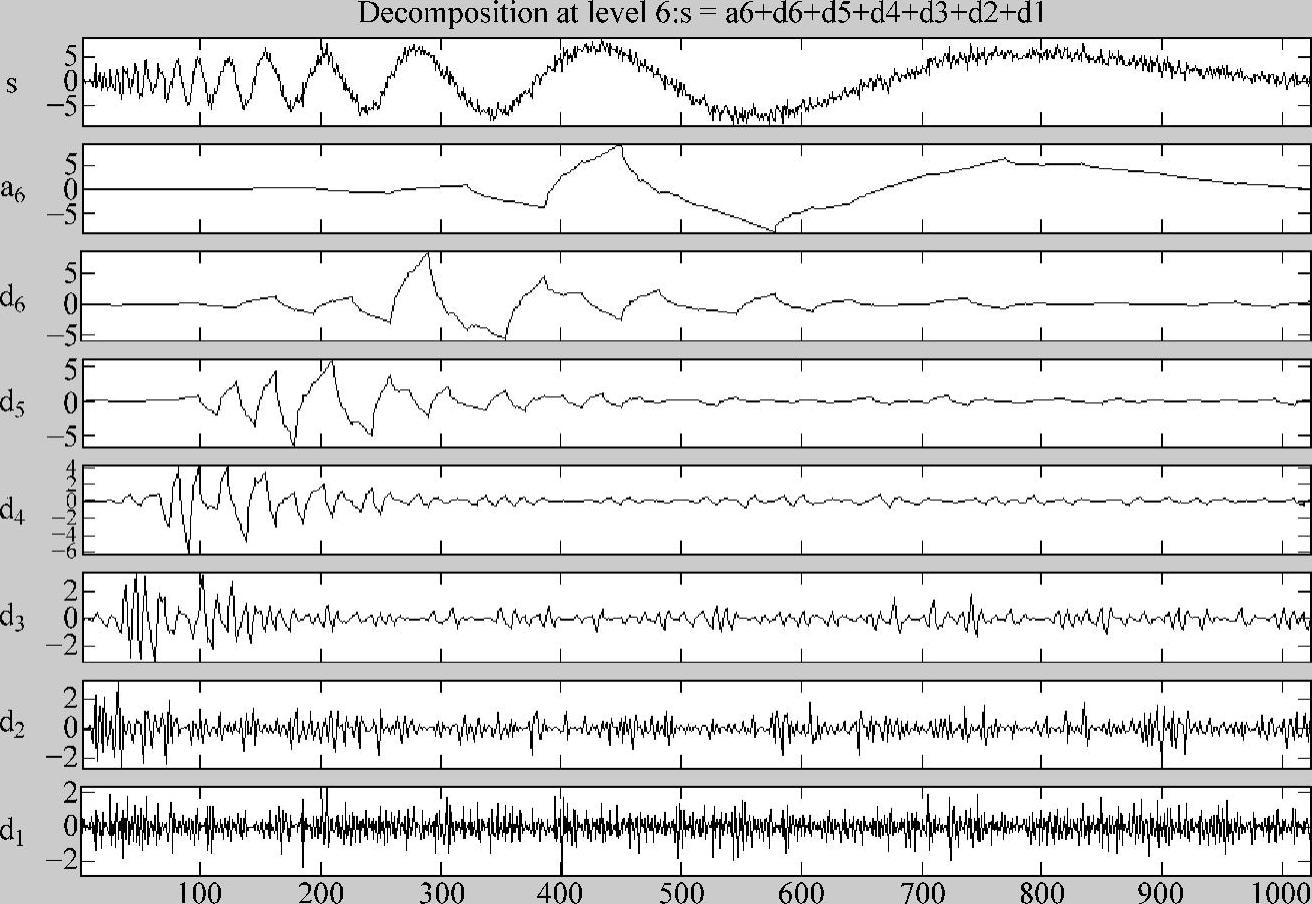
图10-8 一维信号小波分解
图10-9 一维信号小波除噪Simulink模型
对信号除噪的目的就是抑制信号中的噪声部分，从而在信号中恢复有用信号。下面以正弦信号加白噪声为例进行除噪分析。
上述Simulink系统运行结果如图10-10所示。
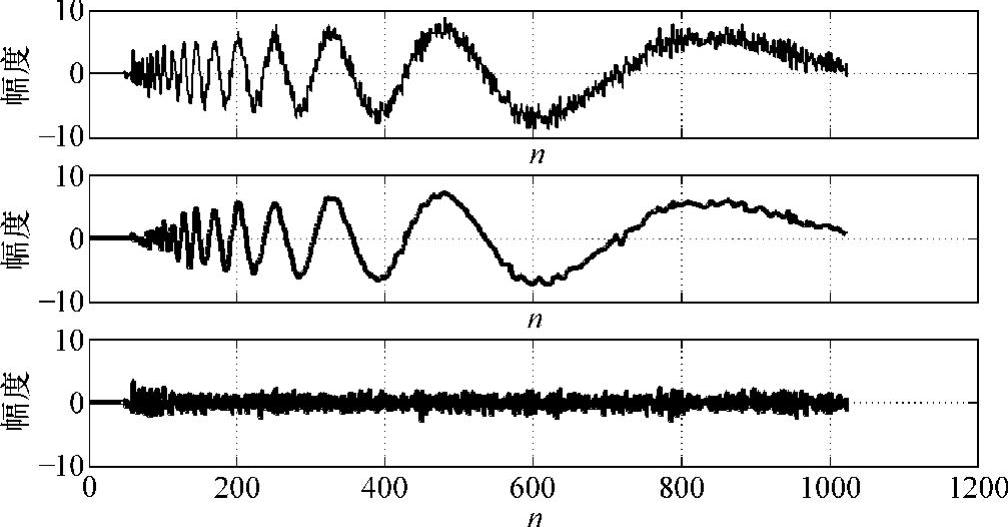
图10-10 一维信号小波除噪
二维信号噪声的消除主要是图像的除噪，主要过程为：首先，二维信号的小波分解即选择合适的小波汉书和分解层次，然后计算信号到最后一层的分解；第二对高频系数进行阈值量化，即对每层的高频系数进行软阈值量化处理；第三，二维小波的重构，根据小波分解的最后一层的低频系数和经过修改的各层高频系数来计算二维信号的小波重构。系统运行结果如图10-11所示。
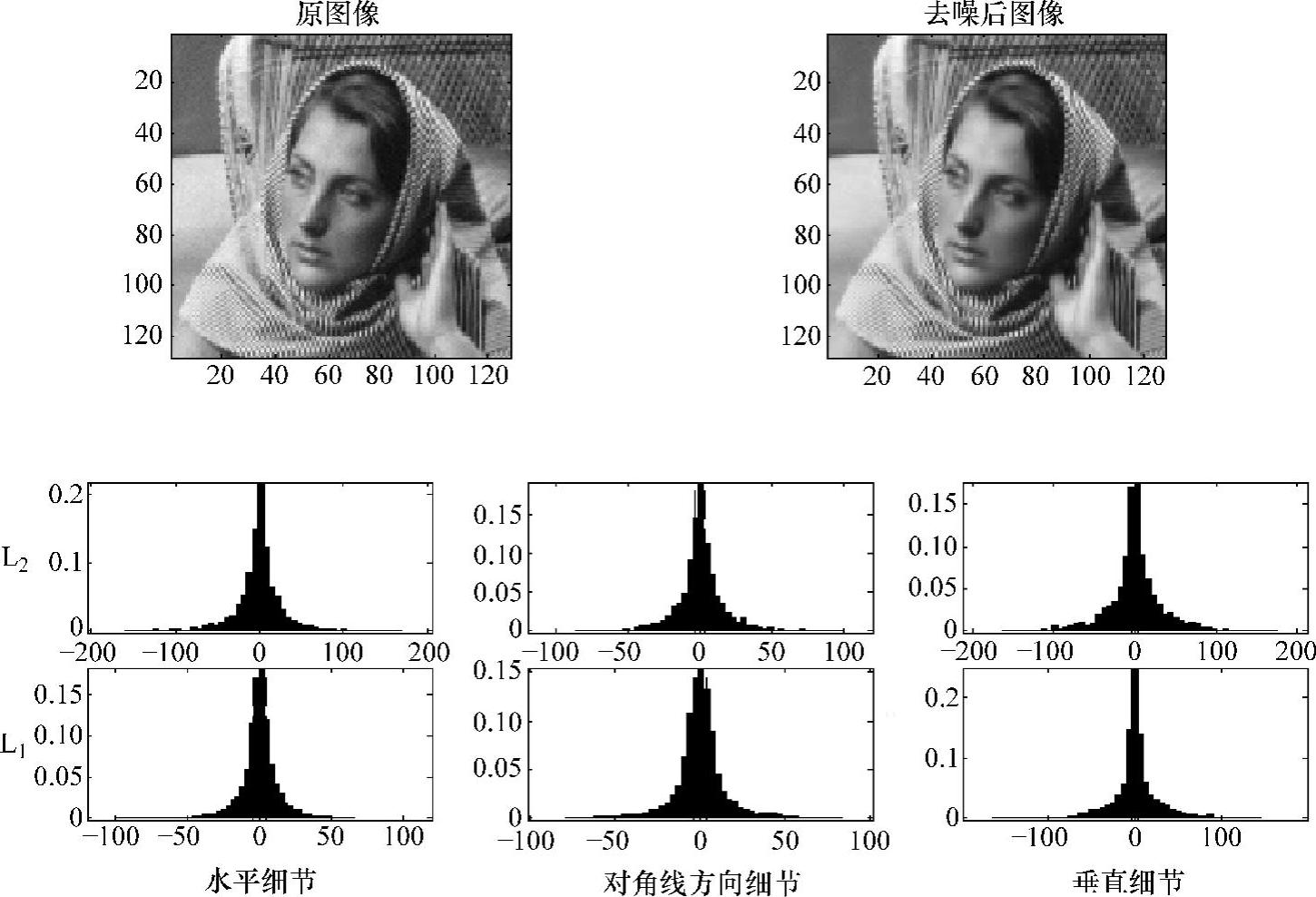
图10-11 二维图像信号小波除噪
有关全相位数字信号处理方法及MATLAB实现的文章
- 详细阅读
-
二维全相位信号处理技术实践详细阅读
参考图5-1的信号移动规律，二维全相位信号处理可以按照行或者列优先的方式来实现，下面以行优先为例给出实现原理图。式表明，二维全相位信号处理对应xi，j的输出等于在行列方向上以xi，j为中心的共2个数据以A为加权的总和。图5-8 二维全相位行信号处理框图图5-8中，输入是按照行方向移动的大小为N×N的数据块，假设待处理图像大小为M×L，且进行边界扩展成×以保证输出图像大小不变。......
2023-06-23
-
数字孪生技术助力城市服务详细阅读
城市服务以人为本，当前较为常见的用户画像局限于少量基础标签和部分行为属性，是数字孪生的初级形态。此外，当服务对象处于某个现实场景当中，将引发人和场景两个数字孪生体间的关联，启动相关的服务，给人提供情景交融、前所未有的惊喜体验。......
2023-10-30
-
DSP数字信号处理器的应用原理与特点详细阅读
DSP以其强大的指令系统及接口功能显示出功能强、速度快、编程和开发方便等特点，广泛应用于通用数字信号处理、通信、语音处理、图像处理和仪器仪表及军事与尖端科技等方面，近年来DSP在自动控制领域也获得广泛应用。DSP芯片已经成为数字电路设计的主要方法。DSP控制的弧焊电源借助DSP实现控制算法和PWM信号发生电路的全数字化，DSP主要完成电压、电流信号的反馈运算、PWM波形的输出、系统实时监控及保护、系统通信等功能。......
2023-06-26
-
全相位数字信号处理方法及MATLAB实现：参详细阅读
用参数模型法进行谱估计首先要选择一种适合被测信号的参数模型，其次用适当的方法估计出模型的参数，最后利用所得到的模型参数计算出信号的谱。因此能否正确选择信号的模型，确定模型的阶数，以及估计模型的参数是决定参数模型法谱估计质量的关键。实际中的许多随机离散时间信号x，都可以表示为有理参数模型。有理系数模型中最常用的是AR模型。，q，则称这种模型为AR模型。......
2023-06-23
-
数字孪生能力模型-数字孪生技术与应用详细阅读
当把数字孪生视为现实世界实体或系统的数字化表现时，更注重架构引领、模型驱动、数据驱动、虚实融合要求。数字孪生的展现能力要求对数字空间中定义的客体的静态和动态内容进行展示。......
2023-10-30
-
航天器数字孪生体：数字孪生技术与应用详细阅读
以航天器数字孪生体为例，其组成元素如图4-1所示。在航天器制造阶段，航天器数字孪生体的演化和完善是通过与产品实体的不断交互开展的。因此，如何实现航天器制造过程数据的实时准确采集、有效信息提取与可靠传输是实现数字孪生体的前提条件。......
2023-10-30
-
数字控制技术及其应用详细阅读
数字控制技术简称数控技术，顾名思义就是以数字的形式实现控制的一门技术。可以用图7-1来描述数控设备的一般形式。图7-1 数控设备的一般形式在图7-1中，A为被加工物的图样，图样上的数据大致分为两类:几何数据和工艺数据。这些数据是指示给数控设备的原始依据。是否采用数控设备，一定要充分考虑其技术经济效果。......
2023-06-28
相关推荐