首页 理论教育WO-LMS算法在自适应辨识中的应用探讨

WO-LMS算法在自适应辨识中的应用探讨

2023-06-23 理论教育 版权反馈
【摘要】：图9-11为一个自适应辨识原理图。图9-12a是8阶自适应滤波器的WO-LMS和LMS算法50次实验的输入自相关分散程度曲线。从图中可见WO-LMS算法比LMS算法有较高的收敛性能，且改善程度随滤波器阶数增加而增大。所以，LMS算法收敛时，自适应滤波器的滤波系数等于被辨识的权矢量。图9-12 WO-LMS和LMS算法输入自相关矩阵的分散比较下面将给出在不同步长时，WO-LMS算法响应收敛曲线和LMS算法收敛曲线的比较。

自适应滤波算法被广泛地应用于系统辨识、回波抵消、自适应谱线增强、自适应信道均衡、语音线性预测、图像自适应滤波等诸多领域。图9-11为一个自适应辨识原理图。图中x（m）表示系统在m时刻的输入信号矢量，M是自适应滤波器权数目，n（m）表示m时刻的干扰噪声，w*表示被辨识系统的权矢量，w（m）是自适应滤波器在m时刻的权矢量，d（m）是m时刻的期望输出值，e（m）=d（m）-wT（m）x（m）是误差信号，y（m）是m时刻的输出。由图9-11可知：

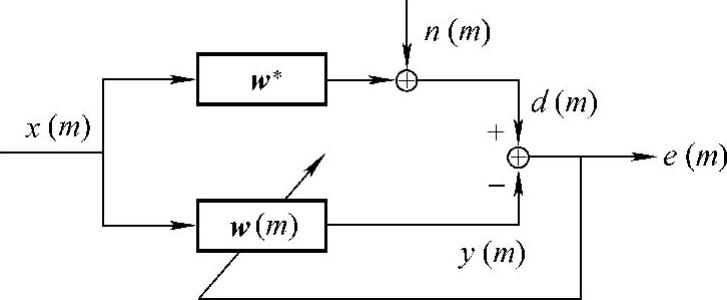
978-7-111-48233-8-Chapter09-60.jpg

图9-11 自适应辨识原理图

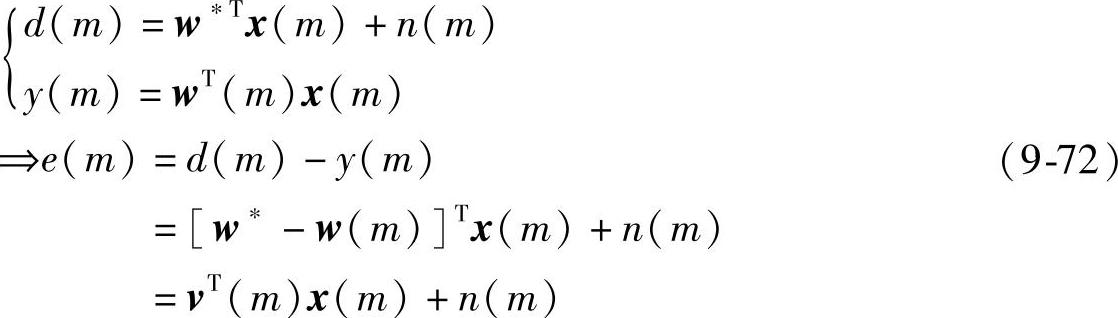
978-7-111-48233-8-Chapter09-61.jpg

因为x（m）与n（m）不相关，所以

ξ（m）=E[e2（m）]=vTRxx v+Rnn （9-73）可以看出，只有v=0即w（m）=w*时，均方误差才取得最小值。所以，LMS算法收敛时，自适应滤波器的滤波系数等于被辨识的权矢量。基于WO算法的自适应辨识系统收敛时的精度比LMS提高很多，模拟实验条件如下：

1）自适应滤波器阶数N=8。

2）未知系统的FIR系数为：h*=[0.9501 0.2311 0.6068 0.4860 0.8913 0.7621 0.4565 0.0185]T。

3）参考输入信号x（n）是高斯白噪声平稳序列，E{x（n）}=0，E{x2（n）}=1。

4）v（n）是与x（n）不相关的高斯白噪声，E{v（n）}=0，E{v2（n）}=0.01。

为了说明WO-LMS算法的收敛性能，实验中首先对WO-LMS和LMS算法输入信号的特征值分散度进行了比较，结果如图9-12所示。图9-12a是8阶自适应滤波器的WO-LMS和LMS算法50次实验的输入自相关分散程度曲线。从图中可见WO-LMS算法比LMS算法有较高的收敛性能，且改善程度随滤波器阶数增加而增大。图9-12b是3～18阶滤波器LMS算法与WO-LMS算法分别进行50次独立实验统计平均谱分散程度比曲线。

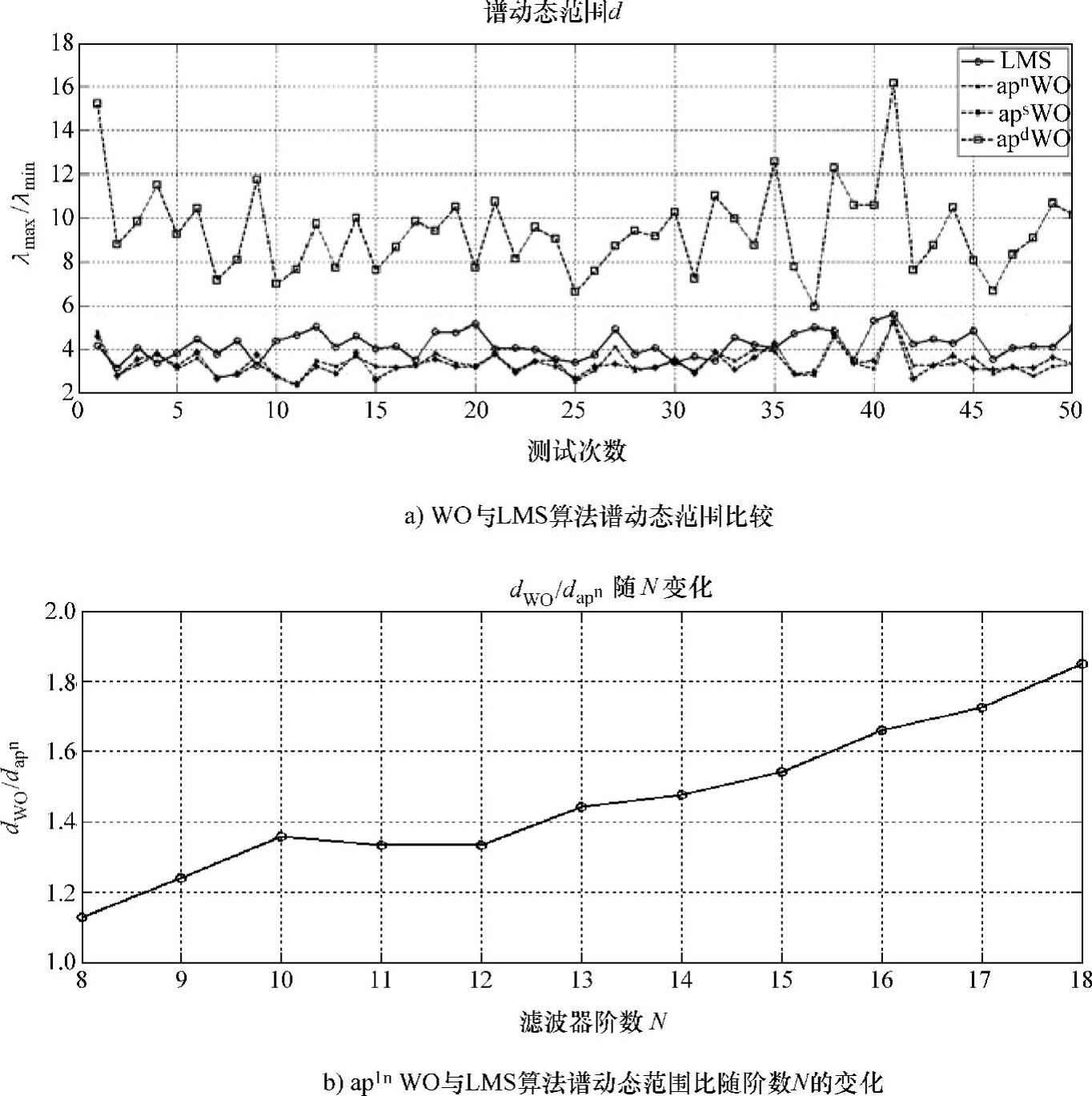
978-7-111-48233-8-Chapter09-62.jpg

图9-12 WO-LMS和LMS算法输入自相关矩阵的分散比较

下面将给出在不同步长时，WO-LMS算法响应收敛曲线和LMS算法收敛曲线的比较。曲线横坐标为迭代次数，纵坐标以系数误差分贝10log10[‖h-h*‖]作为算法收敛的性能指标（独立进行50次实验，每次实验1000个样本点），如图9-13所示。

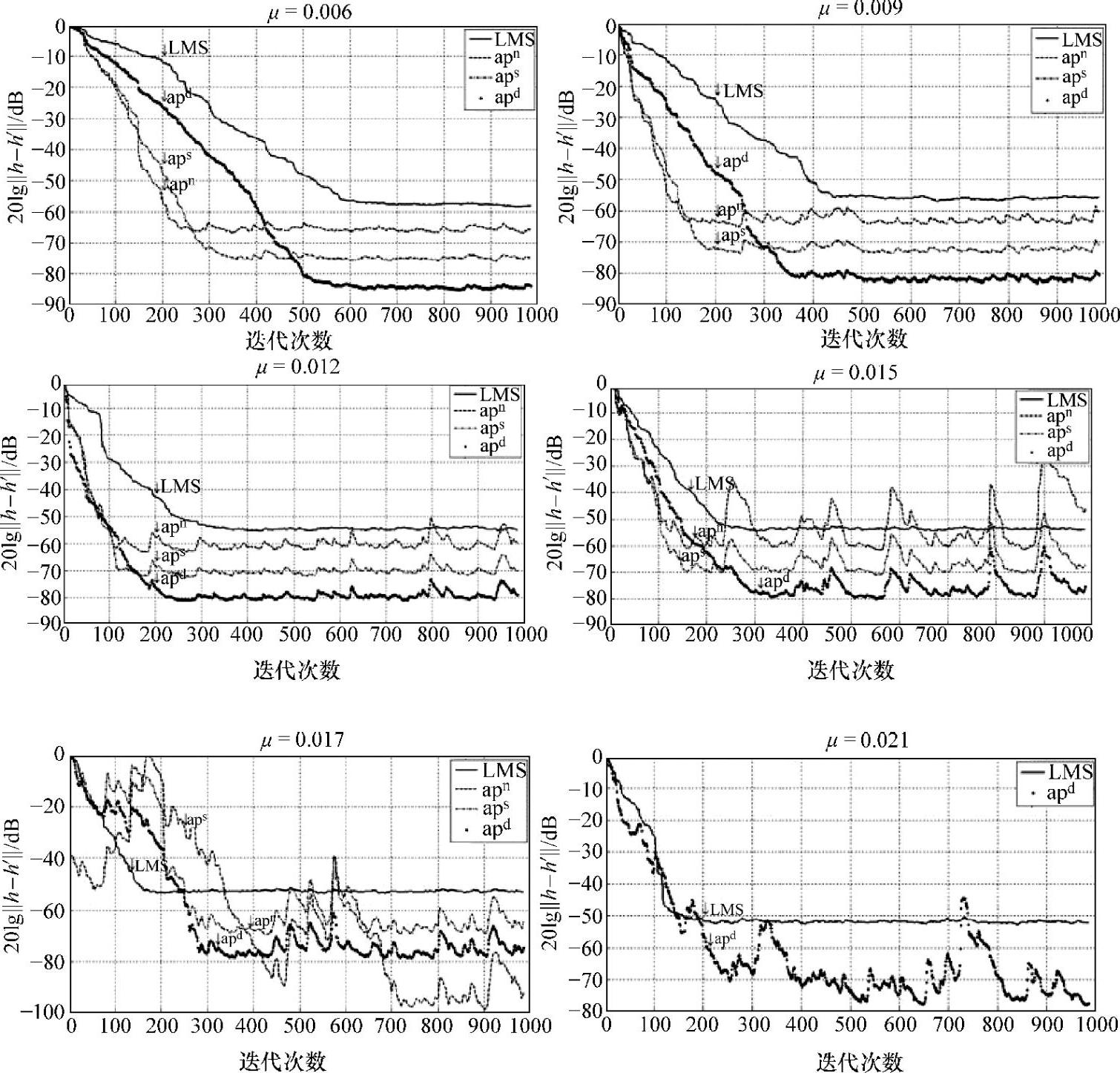
978-7-111-48233-8-Chapter09-63.jpg

从图9-13实验结果可以看出，在步长较小时WO-LMS比LMS算法有较高的收敛速度和较低的稳态失调，其中apn和aps收敛速度大于apd，但apd具有比apns低得多的稳态失调且步长越小这种优势越明显；随着步长增大，使得apnsd稳态时失调摆动增大但仍明显低于LMS算法；μ=0.021时apns算法已经发散而apd算法有相当的收敛速度而稳态失调低于LMS算法近20dB。实现上面实验MAT- LAB代码如下：

978-7-111-48233-8-Chapter09-64.jpg

图9-13 不同μ值WO-LMS算法和LMS算法系数收敛曲线对比

978-7-111-48233-8-Chapter09-65.jpg

978-7-111-48233-8-Chapter09-66.jpg

对于WO-TLMS的测试，选用的3种正交变换为DFT和DCT，实验条件如下：

1）自适应滤波器阶数N=8。

2）未知系统的FIR系数为：h*=[0.95010.23110.60680.48600.8913 0.76210.45650.0185]T。

3）参考输入信号x（n）是高斯白噪声平稳序列，E{x（n）}=0，E{x2（n）}=1。

4）v（n）是与x（n）不相关的高斯白噪声，E{v（n）}=0，E{v2（n）}=0.01。

首先对ap1nsd系统在分别采用FFT和DCT两种正交变换情况下对输入信号的谱动态范围进行比较。分别进行50次独立的实验，每次实验样本点为1000点。实验结果如图9-14所示（曲线纵坐标表示WO-TLMS算法对TLMS算法中输入信号的谱动态范围之比，横坐标是实验次数）。

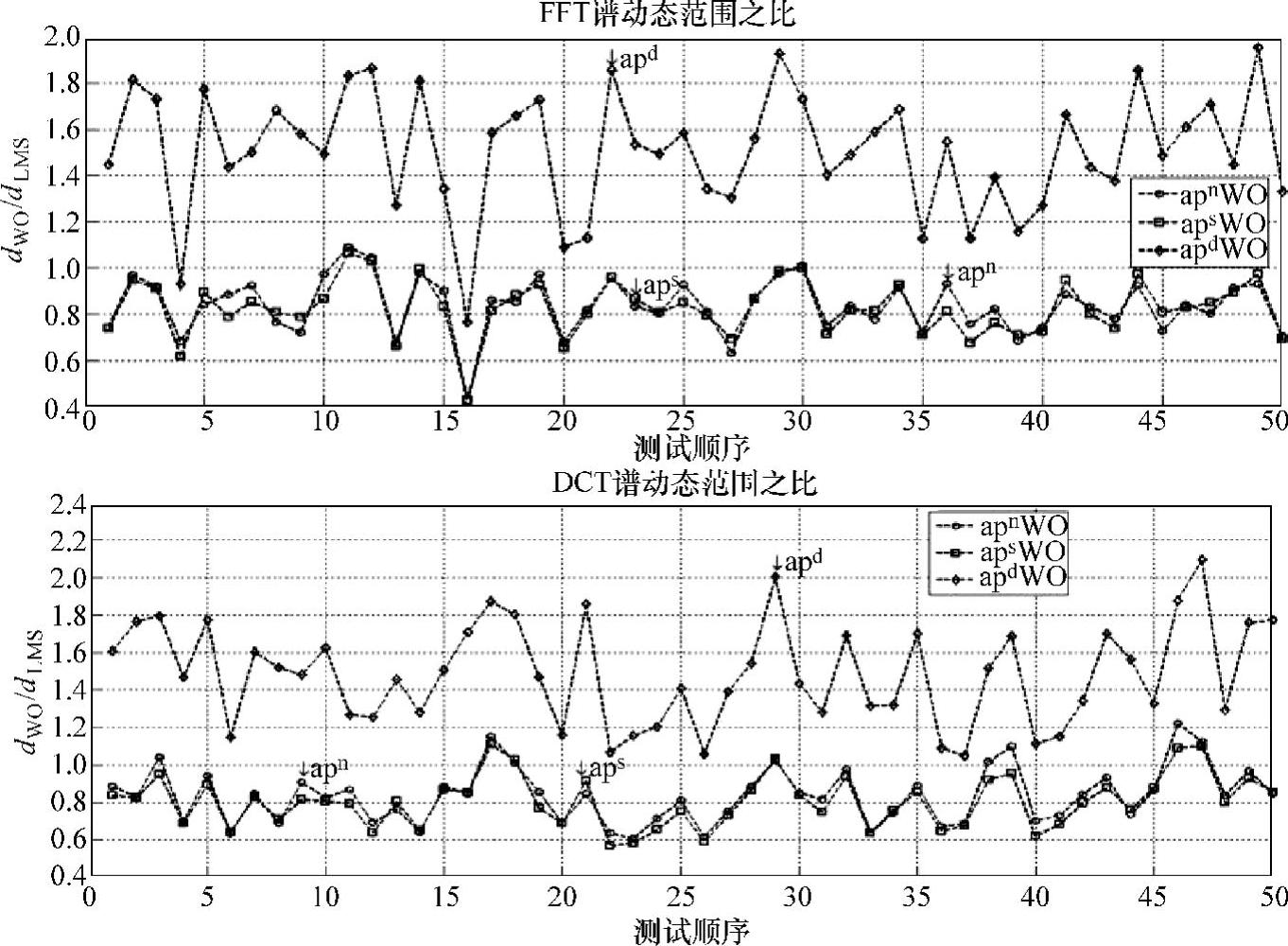
978-7-111-48233-8-Chapter09-67.jpg

图9-14 FFT/DCT ap1nsd WO-TLMS与TLMS谱动态范围比

由图9-14可以看出，两种正交变换下apns WO-TLMS算法中对输入信号的处理都使得谱动态范围小于传统TLMS算法。apd使得收敛速度变慢，分散度最大偏离TLMS算法的2倍左右；DCT对收敛性能的改善同DFT基本相当。

下面给出apnsd WO-TLMS算法收敛曲线和TLMS算法的收敛曲线对比。分别进行50次独立实验，每次实验样本点为1000，然后求其统计平均得出学习曲线，如图9-15所示。曲线的横坐标表示迭代次数，纵坐标以系数分贝误差。参数选取步长μ=0.025，功率归一化因子α=0.8。

由图9-14和图9-15可以看出，两种正交变换下apns WO-TLMS算法的收敛速度大于TLMS而且稳态误差也小于TLMS算法；apd WO-TLMS算法的收敛速度低于TLMS，但它可以获得比TLMS低得多的稳态失调，而且两种正交变换中双窗算法的稳态误差都低于无窗和单窗算法。FFT得到的曲线收敛精度较高但收敛速度慢，DCT具有较快的收敛速度但稳态误差明显低于DFT。表9-1是各算法达到稳态后的权系数估值（精确到小数点后4位）。

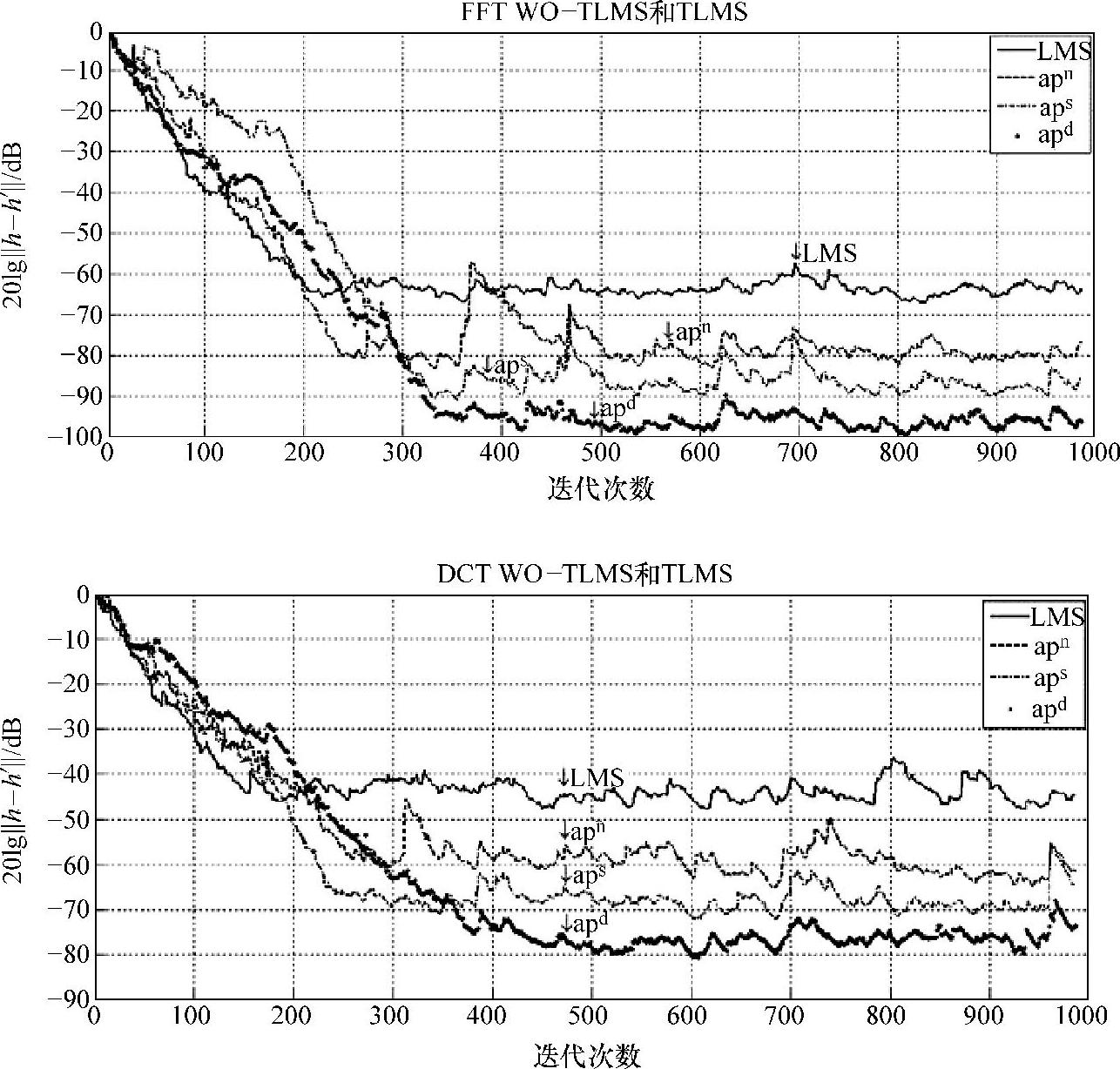
978-7-111-48233-8-Chapter09-68.jpg

图9-15 FFT/DCT apnsd WO-TLMS与TLMS学习曲线

表9-1FFT/DCTap1nsdWO-TLMS算法与TLMS算法稳态估值

978-7-111-48233-8-Chapter09-69.jpg

由上面时域和变换域WO-TLMS在自适应辨识中的应用可以看出，ap1nsd系统对应的WO算法都明显提高了收敛精度。其中ap1d具有最好的估值精度，但收敛速度低于ap1ns；ap1n的收敛速度最快，但精度低于ap1sd。由于在自适应辨识中，主要关注的是收敛后的稳态误差大小，因此，ap1d WO-TLMS算法是较为理想的改善方案。

实现上面实验的MATLAB代码（同时实现时域和频域）如下：

978-7-111-48233-8-Chapter09-70.jpg

978-7-111-48233-8-Chapter09-71.jpg

978-7-111-48233-8-Chapter09-72.jpg

978-7-111-48233-8-Chapter09-73.jpg

有关全相位数字信号处理方法及MATLAB实现的文章

  • 自适应滤波算法及其应用 自适应滤波算法及其应用

    衡量一种自适应算法的优劣一般有两个衡量标准，即参数收敛速度和收敛以后的稳态误差。这种情况下自适应滤波器大部分时间处在未收敛状态，收敛后的精度就显得不太重要。这种算法常采用最小二乘准则即把块内的误差平方求和后要求其和最小，自适应算法的速度和精度的矛盾可以在分块算法中得到体现。......

    2023-06-23

    详细阅读
  • 频率敏感参数辨识在工程应用中的需求 频率敏感参数辨识在工程应用中的需求

    已有的研究工作表明，系统发电机的惯性时间常数、调速器参数、负荷的相关参数等对频率特性曲线均具有一定的敏感性和调整作用，通过参数辨识和调整这些参数，可以使仿真轨迹更接近于实测轨迹[5～7]，进而得到更为符合电力系统运行实际情况的仿真结果。......

    2023-06-29

    详细阅读
  • 自适应滤波器在实际应用中的作用 自适应滤波器在实际应用中的作用

    自适应滤波器的应用主要有以下3种形式：1）如图9-1所示的联合过程估计。这种自适应滤波器常用于ADPCM语音编码。接收端利用同样的自适应滤波器得到y，然后加上接收到的e即得x。其中自适应滤波器的作用是估计输入信号的统计特性，这种自适应滤波器应用于声码器。自适应滤波得到声音信号的参量，通信中只传输参量。图9-2 自适应预测图9-2 自适应预测图9-3 自适应参数估计图9-3 自适应参数估计......

    2023-06-23

    详细阅读
  • 时空域算法在视频分割中的应用 时空域算法在视频分割中的应用

    监控摄像头通常固定安装，并且力图监控更为宽广的视觉区域，视频背景基本不会发生变化，运动片段由运动目标的移入、移出，以及在监视区域内的运动形成的。在微小物体长时间运动后，像素累积变化会对分割结果造成影响。因此，视频运动片段的分割主要取决于运动目标移入和移出监控区域，而与目标在监控区域内的运动状态无关。......

    2023-11-23

    详细阅读
  • PBL在旅游管理专业中的应用探讨 PBL在旅游管理专业中的应用探讨

    （二）PBL在旅游管理专业中应用的必要性分析大部分旅游高等院校将人才培养目标定位为“培养旅游业界中高级管理人才”。其次，PBL教学法与旅游管理专业应用性的学科特点相适应。再次，PBL教学法所具有的优点与旅游管理专业学生所要求具备的核心能力相吻合。鉴于年轻的旅游学科地位较低，大多数高等院校对旅游管理专业的资源倾向不够，所以，是否购置充足的教学设备和资源是决定PBL教学法在旅游管理专业中能否有效实施的重要因素。......

    2023-11-27

    详细阅读
  • 自适应阈值改进的SUSAN算法 自适应阈值改进的SUSAN算法

    Smith和Brady［171］提出的SUSAN算法是一种应用广泛的基于图像灰度变化的方法，随后出现的MIC算法［172］等都是它的思想的改进和发展。SUSAN算法就是根据各个待考察点的USAN区域面积来判断当前点是区域内部点、边界点还是角点。图4-7 USAN区域图解图4-8所示为SUSAN算法的三种近似圆形模板，在实际应用中，37邻域的7×7模板最为常用。灰度差阈值t决定了SUSAN算子所能检测到的最小的对比度以及去除噪声点的能力。......

    2023-06-28

    详细阅读
  • 自适应滑模控制器在信息安全中的应用 自适应滑模控制器在信息安全中的应用

    ，sn]T 是滑动曲面向量。当系统在滑模面上运动时，如下的等式必须成立[155，156]：由式（4-9）可知，当（A，I）可控时，利用极点配置技术，总存在增益矩阵K，使得矩阵（A-K）的所有特征值的实部均为负数。根据线性稳定性判定准则，式（4-5）成立，并且方程（4-9）的收敛速度由矩阵K来决定。为了保证滑模运动的发生，设计的控制器如下：下面证明自适应滑模控制器能够保证滑模运动的发生，控制系统（4-1）和系统（4-2）达到投影同步。......

    2023-11-22

    详细阅读
  • KMeans算法在医药领域的应用 KMeans算法在医药领域的应用

    KMeans可能由于初始值选择的不同，导致最终的结果不同。图4-4KMeans算法迭代过程假设对于相同的样本数据，若随机选择的两个初始点为序号4和7。对于同一个数据集，由于KMeans算法对初始选取的聚类中心敏感，因此可用该准则评价聚类结果的优劣。通常，对于任意一个数据集，KMeans算法无法达到全局最优，只能达到局部最优。......

    2023-11-08

    详细阅读