将这种对信号的加权重叠预处理思想运用于以LMS为准则的自适应滤波算法中，提出加权重叠LMS自适应滤波算法。与LMS相比，它提高了收敛速度同时使稳态失调大为降低。结合横向LMS滤波器结构，得到相应的WO-LMS系统如图9-9所示。图9-9 WO-LMS自适应滤波器信号流图图9-9中，x=[x…......
2023-06-23
改进的权重叠加LMS算法：9.5变换域WO-TLMS
【摘要】：针对这种情况，本节提出了使用加权重叠滤波的思想以克服上述缺点，以改进传统变换域自适应算法的收敛性能。令Et x=z，采用同普通LMS自适应滤波器相类似的方法可得WO-TLMS自适应滤波器权矢量的维纳解wopt和相应的最小均方误差εmin分别为式中，E t=QET=QOW。WO-TLMS中加权重叠矩阵对自适应算法的改善效果与WO-LMS一样，但采用不同的正交变换对系统性能的改善程度也会不同。
变换域自适应滤波的概念是由Dentino等人于1979年首先提出的，其基本思想是把时域信号通过正交变换转变为变换域信号后采用自适应算法。其基本步骤是：①选择正交变换，把时域信号变换成变换域信号；②变换后的信号能量归一化；③采用某一自适应算法进行滤波。常用的正交变换有离散傅里叶变换、离散余弦变换、离散正弦变换、离散小波变换以及沃尔什-哈达玛等。
经过正交变换后的输入信号的自相关矩阵基本上具有稀疏带状结构，从而提高了收敛速度。但由于变换是基于信号分段进行的，因此在输出分段拼接处会出现混叠而失真，并在随后的自适应估计中产生较大的误差而影响算法的收敛性能。针对这种情况，本节提出了使用加权重叠滤波的思想以克服上述缺点，以改进传统变换域自适应算法的收敛性能。加权重叠变换域自适应滤波器可以用图9-10所示。
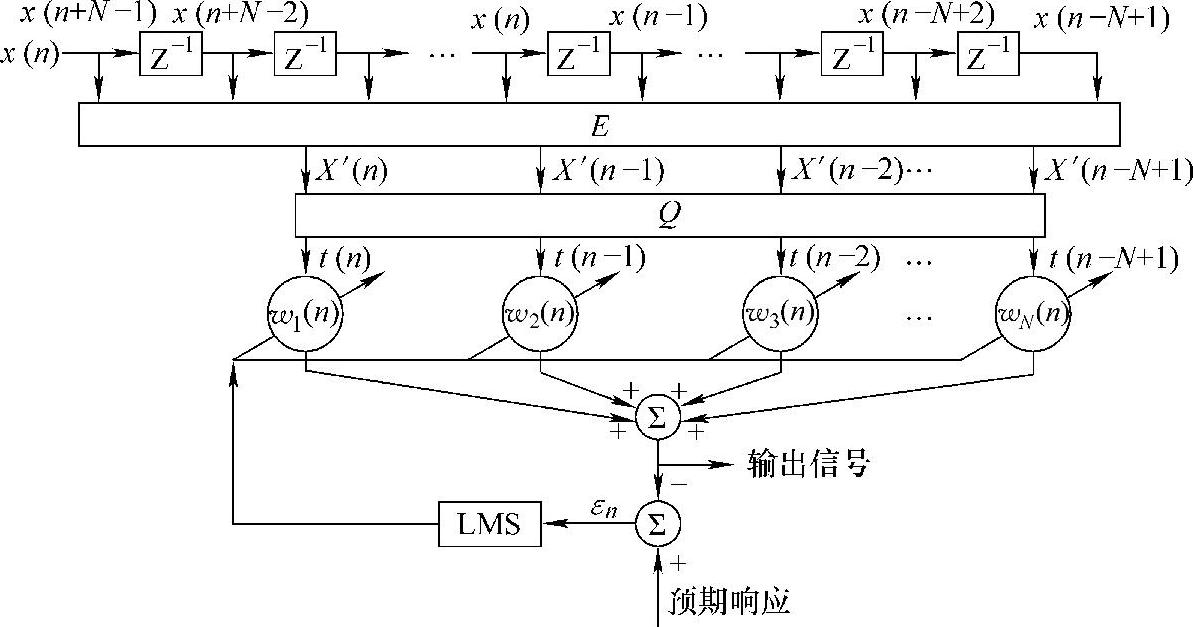
图9-10 WO-TLMS自适应滤波器信号流图
图9-10中E是全相位转移矩阵，Q是N×N阶的正交矩阵，t（n）是正交变换的输出。由图9-10可以看出，自适应过程可以分4步进行：第一，对输入加窗重叠；第二，正交变换；第三，求出输出和误差；第四，系数调整。以上过程可以表示如下：
式中，μ-=diag（μ0…μN-2 μN-1），其中任一元素由下式求出：
μi=μ/Pn（i）i=0，1，…，N-1（9-67）
式中，μ是调节步长；Pn（i）是n时刻第i个频点输入功率的估值，可由下述递推公式求出：
Pn+1（i）=（1-α）Pn（i）+α|Tn（i）|2 （9-68）
式中，Tn是tn的正交变换；α是常数。由式（9-66）～式（9-68）可以得到：
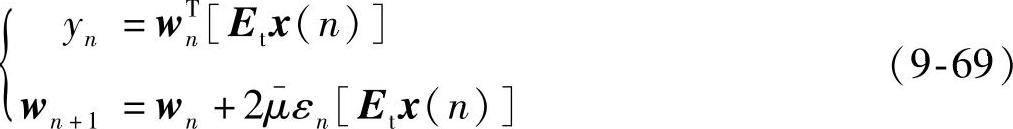
式中，E t=QET=QOW。由上面的结果可以看出，带窗重叠变换域自适应的滤波器的变换矩阵等于E t。令Et x（n）=z（n），采用同普通LMS自适应滤波器相类似的方法可得WO-TLMS自适应滤波器权矢量的维纳解wopt和相应的最小均方误差εmin分别为
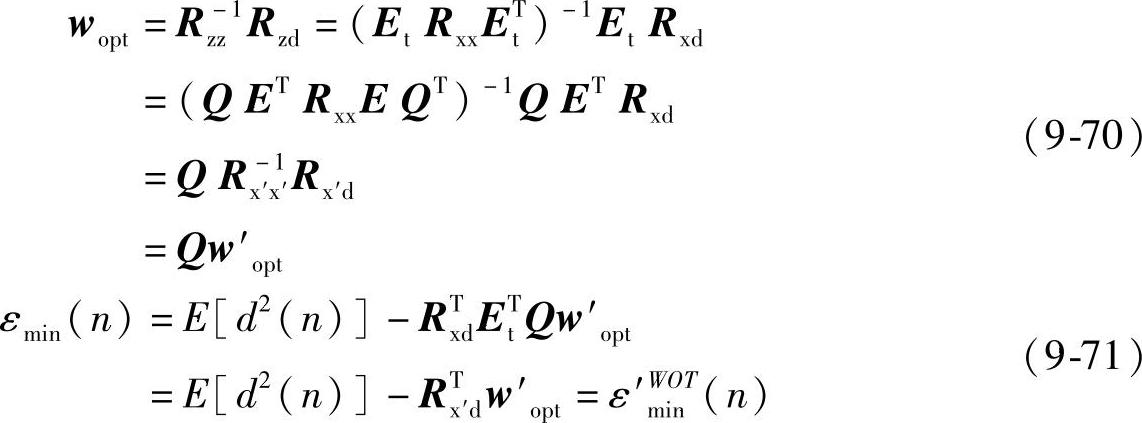
式中，w′opt和εmin（n）分别是输入为x′（n）时正交变换LMS自适应滤波器权矢量维纳解与相应最小均方误差。WO-TLMS中加权重叠矩阵对自适应算法的改善效果与WO-LMS一样，但采用不同的正交变换对系统性能的改善程度也会不同。
有关全相位数字信号处理方法及MATLAB实现的文章
- 详细阅读
-
形状特征的分析与应用：空间域与变换域的几何特详细阅读
形状特征可以分为空间域几何特征和变换域几何特征两个大类。形状的小波表示方式在粗尺度上给出形状的全局信息，在细尺度上给出局部信息。......
2023-06-28
-
自适应阈值改进的SUSAN算法详细阅读
Smith和Brady［171］提出的SUSAN算法是一种应用广泛的基于图像灰度变化的方法，随后出现的MIC算法［172］等都是它的思想的改进和发展。SUSAN算法就是根据各个待考察点的USAN区域面积来判断当前点是区域内部点、边界点还是角点。图4-7 USAN区域图解图4-8所示为SUSAN算法的三种近似圆形模板，在实际应用中，37邻域的7×7模板最为常用。灰度差阈值t决定了SUSAN算子所能检测到的最小的对比度以及去除噪声点的能力。......
2023-06-28
-
最小均方LMS算法优化方案详细阅读
按照自适应滤波系数矢量的变化与梯度矢量方向之间的关系，可写出LMS算法的公式如下：因为，所以这种瞬时估计法是无偏的。图9-6 自适应LMS算法信号流图由此可见，自适应LMS算法简单，它既不需要计算输入信号的相关函数，也不要求矩阵可逆。但是，由于LMS算法采用梯度矢量的瞬时估计值，它有较大的方差以致不能获得最优滤波性能。下面从收敛性、学习曲线和失调3个方面分析LMS算法的收敛性能。......
2023-06-23
-
基于LMS准则的基窗设计算法优化详细阅读
为寻找更为理想的基窗函数，借助LMS算法思想提出了“基于LMS准则以apSW为模型的基窗函数设计方法”。图3-21 余弦基神经自适应网络图3-21 余弦基神经自适应网络图3-22 apSW基窗LMS设计算法按照流程图，设计截止频率为π/4的32阶低通apSW的窗函数F。......
2023-06-23
-
改进NSGA-Ⅱ的优化算法设计方案详细阅读
MNSGA-Ⅱ具体流程如图9-12所示。MNSGA-Ⅱ以天线资源作为编码依据，在完成对任务的调度预处理之后，将任务所选择的天线资源序号作为种群内染色体基因。图9-13初始种群构造流程2）改进NSGA2算子设计快速非支配排序。......
2023-07-02
-
基于霍夫变换的目标检测算法详细阅读
基本的霍夫变换最初是用来进行直线检测的，而广义霍夫变换则可以在所需检测的曲线或目标轮廓没有或不易用解析表达式时，利用表格来建立曲线或轮廓点与参考点间的关系，进而检测出目标［67］。霍夫变换的突出优点就是可以将图像中较为困难的全局检测问题转换为参数空间中相对容易解决的局部峰值检测问题。......
2023-06-28
-
变换域全相位信号处理优化技巧详细阅读
图4-12 变换域信号处理图对于N阶系统，时刻n输入xn=[x，x（n-1），…其中X1是1维N阶全相位输入信号，即式就是全相位数字信号处理得到的输出与输入的数学关系表达。把式称为全相位变换，矩阵A称为全相位变换基，矩阵T则为全相位变换核。综合以上，变换域全相位数字信号处理一种可能实现如图4-16所示。......
2023-06-23
相关推荐