最小均方LMS算法优化方案

2023-06-23 理论教育版权反馈

【摘要】：按照自适应滤波系数矢量的变化与梯度矢量方向之间的关系，可写出LMS算法的公式如下：因为，所以这种瞬时估计法是无偏的。图9-6 自适应LMS算法信号流图由此可见，自适应LMS算法简单，它既不需要计算输入信号的相关函数，也不要求矩阵可逆。但是，由于LMS算法采用梯度矢量的瞬时估计值，它有较大的方差以致不能获得最优滤波性能。下面从收敛性、学习曲线和失调3个方面分析LMS算法的收敛性能。

最陡下降算法不需要知道误差特性曲面的先验知识，其算法就能收敛到最佳维纳解且与起始条件无关。但是最陡下降算法的主要限制是它需要准确测得每次迭代的梯度矢量，这妨碍了它的应用。为了减少计算复杂度和缩短自适应收敛时间，1960年，美国斯坦福大学的Widrow等人提出了LMS算法，这是一种用瞬时值估计梯度矢量的方法，即

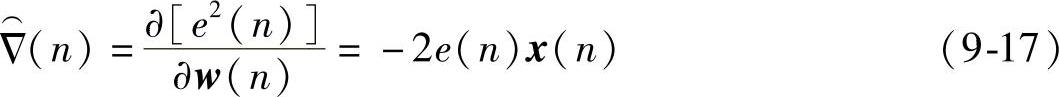
因为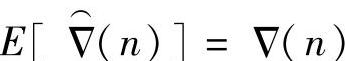，所以这种瞬时估计法是无偏的。按照自适应滤波系数矢量的变化与梯度矢量方向之间的关系，可写出LMS算法的公式如下：

把式（9-5）代入到式（9-18）中得：

由式（9-19）可以得到自适应LMS算法的信号流图，如图9-6所示。这是一个具有反馈形式的模型，如同最陡下降法，利用时间n=0的滤波系数矢量为任意的起始值w（0），然后开始LMS算法的计算，其步骤如下：

1）由现在时刻n的矢量估值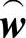（n）、x（n）以及期望信号d（n）按照式（9-5）计算误差信号e（n）。

2）利用递归算法计算滤波器系数矢量的更新估值。

3）将时间指数n增加1，重回到步骤1）执行直到达稳态为止。

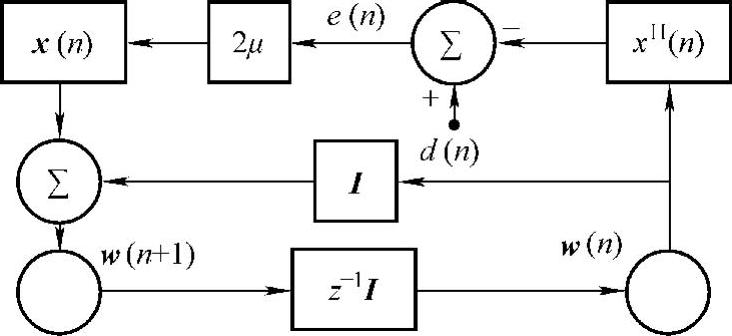
图9-6 自适应LMS算法信号流图

由此可见，自适应LMS算法简单，它既不需要计算输入信号的相关函数，也不要求矩阵可逆。但是，由于LMS算法采用梯度矢量的瞬时估计值，它有较大的方差以致不能获得最优滤波性能。下面从收敛性、学习曲线和失调3个方面分析LMS算法的收敛性能。

1.自适应收敛性

自适应滤波器系数矢量的起始值w（0）是任意常数，应用LMS算法调节滤波系数具有随机性而使矢量w（n）带来非平稳过程，通常为了简化LMS算法的统计分析，往往假设算法连续迭代之间存在以下的充分条件：

1）每个输入信号样本矢量x（n）与其过去全部样本矢量x（k），k=0，1，…，n-1统计独立且不相关，即E[x（n）x^H（k）]=0。

2）每个输入信号样本矢量x（n）与全部过去的期望信号d（k），k=0，1，…，n-1统计独立且不相关，即E[x（n）d^H（k）]=0。

3）期望信号样本d（n）依赖于输入过程样本矢量x（n），但全部过去的期望信号样本统计独立。

4）滤波器抽头输入信号矢量x（n）与期望信号d（n）包含着全部n个共同的高斯分布随机变量。

在上述假设的前提下，自适应滤波器在n+1时刻的滤波系数矢量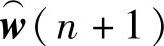依赖于3个输入：①输入过程的过去样本矢量x（k），k=0，1，…，n-1；②期望信号的以前样本值d（k），k=0，1，…，n-1；③滤波系数矢量的起始值。

对式（9-19）两端求数学期望，可得到：

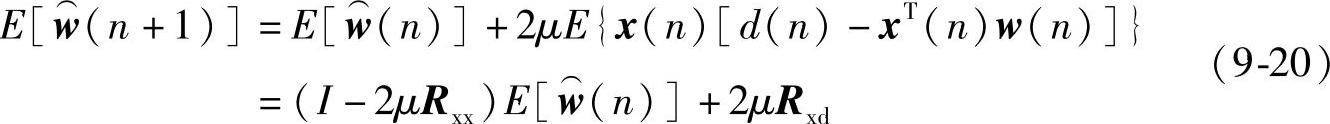
当k=0时，利用式（9-20）可求得：

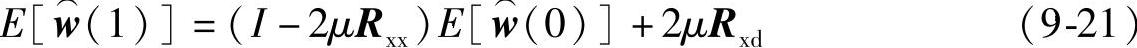
当k=1时，利用式（9-21）的结果可得：

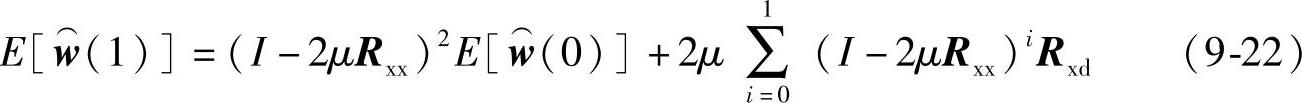
依次递推就得到通式如下：

式中，R_xx是Hermite矩阵，其特征值分解式可写成如下：

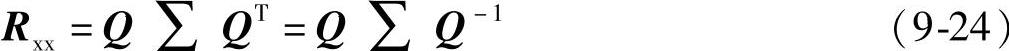
式中，Q是正定特征矩阵；∑==diag（λ₀，λ₁，…，λ_M）是特征值对角阵，λ_i是R_xx的特征值。把式（9-24）代入到式（9-23）并注意到E[w⌒（0）]=w⌒（0），所以得：

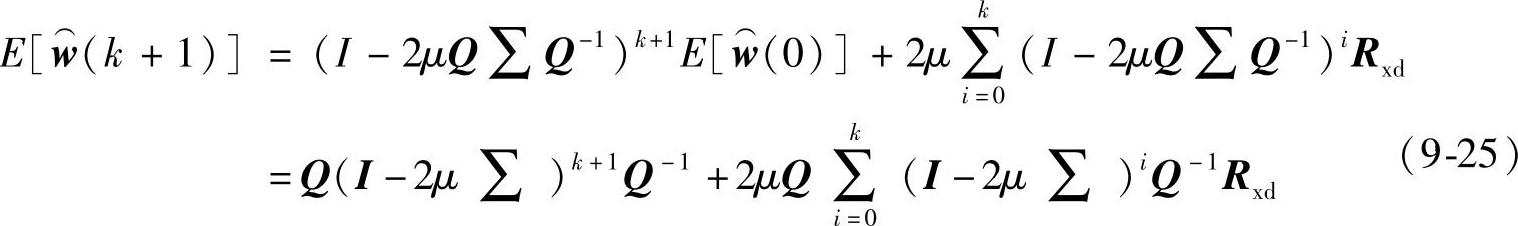
显然，当迭代次数k增加到很大时，式（9-25）收敛的条件是：I-2μ∑的对角线元素均大于0且小于1，即要求满足：

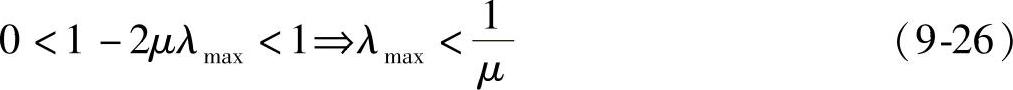
式中，λ_max是R_xx的最大特征值；μ是收敛因子或步长。把最大特征值与最小特征值的比值d=λ_max/λ_min称为谱动态范围，它决定着收敛速度，d越大收敛速度越小。降低d的方法之一是产生正交数据。在条件（9-26）满足的条件下，式（9-25）等于：

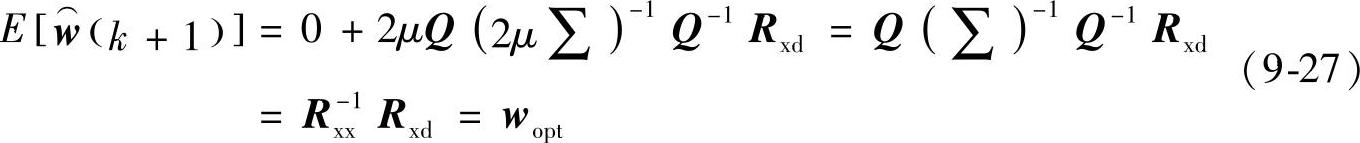
2.平均MSE———学习曲线

最陡下降法每次迭代都要精确计算梯度矢量，使自适应横向滤波器权矢量或滤波系数矢量w（n）能达到最佳维纳解w（0），这时滤波器MSE为最小，即：

ξ_min=σ²_d-w^TP （9-28）

式中，σ²_d是期望信号d（n）的方差。学习曲线定义为均方误差随迭代计算次数n的变化关系，即

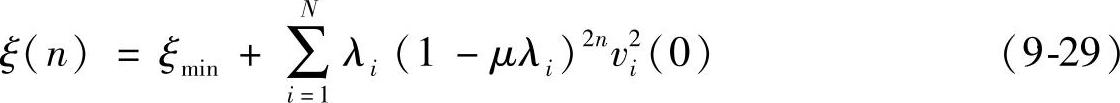
式中，v_i是w（n）正交旋转后对应矢量中的分量。式中每个指数项对应算法的固有模式，模式的数目等于滤波加权数。显而易见，由于上式中1_-μλ_i<1，故当n→∞时最陡下降算法的均方误差ξ（∞）=ξ_min。但LMS算法用瞬时值估计梯度存在误差的噪声估计，结果使滤波器权矢量估值w⌒（n）只能接近维纳解，这意味着滤波均方误差ξ（n）随着迭代次数n的增加而出现小波动地减小，最后ξ（∞）不是等于ξ_min而是稍大于其值，如图9-7所示。如果步长选得越小，则噪化指数衰减曲线上的波动幅度将越小，即学习曲线的平滑度越好。

但是，对于自适应横向滤波器总体来说，假设每个滤波器LMS算法用相同的步长和同样的起始系数矢量，并从同一统计群体随机地选取各个平稳的各态历经的输入信号，由此计算自适应滤波器总体平均学习曲线，如图9-8所示。这是一条平滑的总体平均学习曲线，通常它是由50～200个单独LMS算法的结果加以平均而得到。显然，可以用E[ξ（n）]表示的平均RMS来描述LMS算法的动态性质。

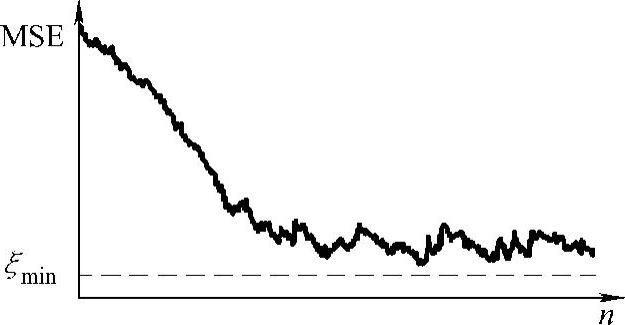
图9-7 单条学习曲线

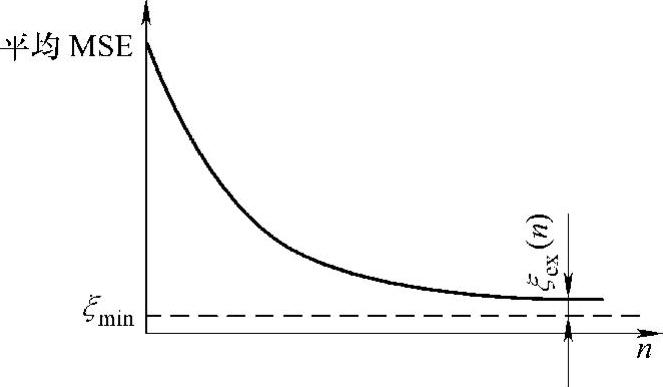
图9-8 总体平均学习曲线

3.失调

在自适应滤波器中，失调χ是衡量其滤波性能的一个技术指标，它被定义为总体平均超量均方误差值ξ_ex（∞）与最小均方误差值ξ_min之比，即

可推导得出：

将式（9-31）结果代入到式（9-30）中得到：

通常步长μ值很小，因此，失调又可近似表示为

由此可以看出，自适应滤波器LMS算法的稳态失调与步长成正比。当步长很小时，失调也降低，但收敛时间也会变长，因此，失调与自适应收敛之间存在着矛盾。

4.缩短收敛过程的方法

由LMS算法的迭代公式（9-18）可以看出，为了缩短收敛过程，可以从3个方面进行设计：

1）采用不同的梯度估值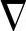（n），如LMS牛顿法，它估计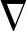（n）时采用了输入矢量相关函数的估值，使得收敛速度大大优于上述经典的LMS算法，因为它在迭代过程中采用了更多的有关输入信号矢量的信息。

2）对收敛因子步长μ选用不同方法。步长μ的大小决定着算法的收敛速度和达到稳态的失调量的大小。对于常数μ值来说，收敛速度和失调量是一对矛盾，要想得到较快的收敛速度可以选用大的μ值，这将导致大的失调量；如果要满足失调量的要求，则收敛速度将受到制约。因此，人们研究了采用变步长的方法来克服这一矛盾。自适应过程开始时，取用较大的步长以保证较快的收敛速度，然后让μ值逐渐减小，以保证收敛后得到较小的失调量。如归一化LMS算法、时域正交化LMS算法等都是采用变步长方法的高效自适应算法。

3）采用变换域分块处理技术。对由滤波器权系数矢量调整的修正项中的乘积用变换域快速算法与分块处理技术可以大大减少计算量，且能改善收敛特性，如频域LMS算法、分块LMS算法等。

最小均方LMS算法优化方案

相关推荐