衡量一种自适应算法的优劣一般有两个衡量标准，即参数收敛速度和收敛以后的稳态误差。这种情况下自适应滤波器大部分时间处在未收敛状态，收敛后的精度就显得不太重要。这种算法常采用最小二乘准则即把块内的误差平方求和后要求其和最小，自适应算法的速度和精度的矛盾可以在分块算法中得到体现。......
2023-06-23
实现最佳自适应滤波：最陡下降法
【摘要】：最陡下降法是实现自适应滤波器最佳搜索的一种优化技术，它利用梯度信息分析自适应滤波性能和追踪最佳滤波状态。式是最陡下降法的数学公式，由此可得到信号流图如图9-5所示。图9-5 最陡下降算法的信号流图图9-5 最陡下降算法的信号流图
最陡下降法是实现自适应滤波器最佳搜索的一种优化技术，它利用梯度信息分析自适应滤波性能和追踪最佳滤波状态。梯度矢量是由均方误差ξ（n）的梯度来定义的，在多维超抛物曲面上任一点的梯度矢量是对应于均方误差ξ（n）对滤波系数wi（n）的一阶导数，由起始点或现在点变化到下一个点的滤波系数变化量正好是梯度矢量的负数。换句话说，自适应过程是在梯度矢量的负方向接连地校正滤波系数的，即在误差性能曲面的最陡下降方向移动和逐步校正滤波系数，最终到达均方误差为最小的碗底最小点，获得最佳滤波或次优工作状态。
令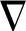
（n）代表n时刻的N×1维梯度矢量，这里N等于滤波器滤波系数个数；w（n）为自适应滤波器在n时刻的滤波系数或权矢量。按照最陡下降法调节滤波系数，则在n+1时刻的滤波系数或权矢量w（n+1）可以用下列简单的递归关系来计算：
w（n+1）=w（n）+μ[-Δ（n）] （9-12）
式中，μ是一个正实数，通常称它为自适应收敛系数或步长。由梯度的定义，Δ（n）可以写成：
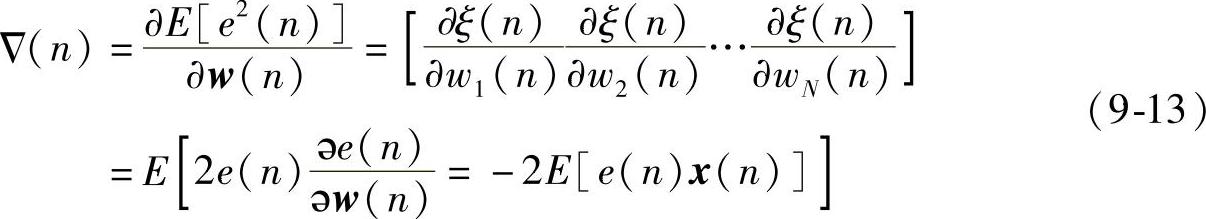
当滤波系数为最佳值即维纳解时，梯度矢量Δ（n）=E[e（n）x（n）]=0。这意味着误差信号与输入信号矢量的每一个分量都正交（即互不相关）。且由式（9-5）不难证明：
E[e（n）y（n）]=0 （9-14）
结合式（9-7）和式（9-13），可求得梯度如下：
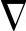（n）=-2P+2Rw（n） （9-15）
因此，在最陡下降法中，当相关矩阵R与互相关矢量P已知时，则由w（n）可以计算梯度矢量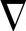
（n），然后将式（9-15）代入到式（9-12）中，可以计算滤波系数的更新值：
w（n+1）=w（n）+2μ[P-Rw（n）] （9-16）
式中，μ是收敛因子。式（9-16）是最陡下降法的数学公式，由此可得到信号流图如图9-5所示。图中，I是N阶单位阵。
图9-5 最陡下降算法的信号流图
有关全相位数字信号处理方法及MATLAB实现的文章
- 详细阅读
-
高斯滤波次数分析的最佳选择详细阅读
本章所提出的方法利用多次高斯滤波来构造原始纹理图像的多尺度图像空间，高斯滤波的次数对本章所提出方法的纹理识别精度和实时性具有重要的影响。从上述两个方面的分析可以看出，过多次数的高斯滤波会导致本章所提出方法的计算量增加和实时性降低。因此，根据表4-1的实验结果及分析，本章方法选择最佳的高斯滤波次数为n=2，此时既能获得最高的纹理识别精度，又能保持较少次数的高斯滤波，从而获得很好的实时性。......
2023-06-29
-
自适应滤波器在实际应用中的作用详细阅读
自适应滤波器的应用主要有以下3种形式：1）如图9-1所示的联合过程估计。这种自适应滤波器常用于ADPCM语音编码。接收端利用同样的自适应滤波器得到y，然后加上接收到的e即得x。其中自适应滤波器的作用是估计输入信号的统计特性，这种自适应滤波器应用于声码器。自适应滤波得到声音信号的参量，通信中只传输参量。图9-2 自适应预测图9-2 自适应预测图9-3 自适应参数估计图9-3 自适应参数估计......
2023-06-23
-
实施三提工程，实现三最目标！详细阅读
实施“三提”工程实现“三最”目标陈铁雄当前，经济发展要把稳增长放在更加重要的位置，越是这个时候，越要突出转作风、抓落实。（二）全面实施“审批提速工程”，努力实现工作节奏最快追求最快是“三提”工程的目标和指向。......
2023-11-28
-
综合评价和策略选择：实现最佳效果详细阅读
持续清洁生产是清洁生产实施的必要环节，保证实施效果得到延续，从而持续地推行清洁生产。综合评价是解决多个目标优化的决策问题，对方案的整体性、全局性进行评价。动态方法对于下一步的策略选择更有利，它可以为确定策略参数提供指导。以系统动力学的方法对清洁生产实施的环境—经济综合效益进行评价，其过程如图3．10所示。图3．10基于系统动力学的CP综合评价和策略选择......
2023-06-20
-
如何设计带通滤波器实现阻抗匹配？详细阅读
带通滤波器由电感L3、L4和电容C8、C9组成，L3、C8构成串联回路，L4、C9构成并联回路。在如图4-28所示的电路中，Rb是功率合成器的输出阻抗，Rc是馈线的特性阻抗，为了实现阻抗匹配，从并联谐振回路电感L2抽头端往负载方向看去的输入阻抗应等于Rb，而从C2上端往带通滤波器方向看去的输出阻抗应等于Rc，回路抽头时Rb、Rc之间的变比关系为：式中，P=L2-1/=L2-1/L2，称为接入系数。......
2023-06-26
-
三相晶闸管充电机的最简实现详细阅读
该线路是利用充电蓄电池的电势来关断晶闸管的，线路的工作条件是蓄电池电势必须大于或等于次级相电压峰值的一半。当蓄电池电势E大于或等于时，晶闸管在每相隔120°电度角内，使晶闸管承受一次正向电压和反向电压或电压为零。图4-12最简单的三相晶闸管充电机线路晶闸管V阴极和阳极之间承受的电压Uv，经电阻R1降压、稳压管VS稍波，在VS两端得到一个与三相同步的梯形同步电源。......
2023-06-20
-
傅里叶光学：逆滤波和图像消模糊的实现详细阅读
式表示的空间滤波器称为逆滤波器。除此之外，逆滤波器还可用计算全息图来制造。采用逆滤波器消模糊又称为无限制的消模糊，它无法解决系统噪声的影响。如果采用加性噪声模型，则式和式应表示为当应用式所示的逆滤波器进行空间滤波处理时，输出平面上的复振幅为上式表明，由于模糊系统的传递函数H存在着一系列零点和弱的高频分量，第二项将变得很大，以至淹没有用的第一项，致使原始物体像得不到恢复。......
2023-11-23
相关推荐