最小均方滤波算法：高效的信号处理方法

2023-06-23 理论教育版权反馈

【摘要】：自适应滤波器的两个重要组成部分中核心是算法，用来调整滤波子系统结构的参数或滤波系数。最小均方横向自适应滤波结构如图9-4所示。，N）进行调节，最终使自适应滤波的目标（代价）函数最小化，达到最佳滤波状态。经过自适应调节过程，使对应于滤波系数变化的点朝碗底最小点方向移动，最终到达碗底最小点得以实现最佳维纳滤波。

当在未知统计特性的环境下处理观测信号或数据以获得所期望的结果时，利用自适应滤波器可以得到令人满意的解，其性能远超过通用方法所设计的固定参数的滤波器。如果一个实用系统含有较多的自适应子系统，则它在自适应学习性能方面将有较高的自适应的先进性。自适应滤波器的两个重要组成部分中核心是算法，用来调整滤波子系统结构的参数或滤波系数。算法是指调节自适应滤波系数的步骤，以达到在所描述准则下的误差最小化。自适应滤波含有两个过程即自适应过程和滤波过程。前一过程的基本目标是调节滤波系数θ（n）使有意义的目标函数或代价函数F（·）最小化，输出信号y（n）逐步逼近所期望的参考信号d（n），由两者之间的估计误差e（n）驱动某种算法对滤波系数进行调整，使滤波器处于最佳工作状态以实现滤波过程。所以，自适应过程是一个闭合的反馈环，算法决定了这个闭合环路的自适应过程所需要的时间。由于目标函数F（·）是输入信号x（n）、参考信号d（n）及输出信号y（n）的函数，因此目标函数必须具有以下两个性质：

1）非负性：F[x（n），d（n），y（n）]≥0 ∀x（n），d（n），y（n）；

2）最佳性：F[x（n），d（n），y（n）]=0　d（n）=y（n）。

在自适应过程中，自适应算法逐步逼近使目标函数F（·）最小化，最终使y（n）逼近于d（n），滤波参数或权系数θ（n）收敛于θ₀即自适应滤波系数的最优解。因此，自适应过程也是自适应滤波器的最佳线性估计过程，既要估计滤波器能实现期望信号d（n）输出的整个过程，又要估计滤波权系数以进行有利于主要目标方向的调整。这些估计过程是时变的，这就是自适应滤波器需要有的自适应收敛过程。

最小均方横向自适应滤波结构如图9-4所示。图中x（n）是输入信号，y（n）是输出信号，d（n）为y（n）想要趋近的理想信号且为已知，e（n）为误差信号。假设两个条件：1）输入信号x（n）和d（n）是广义平稳的；2）x（n）和d（n）的统计特性已知。

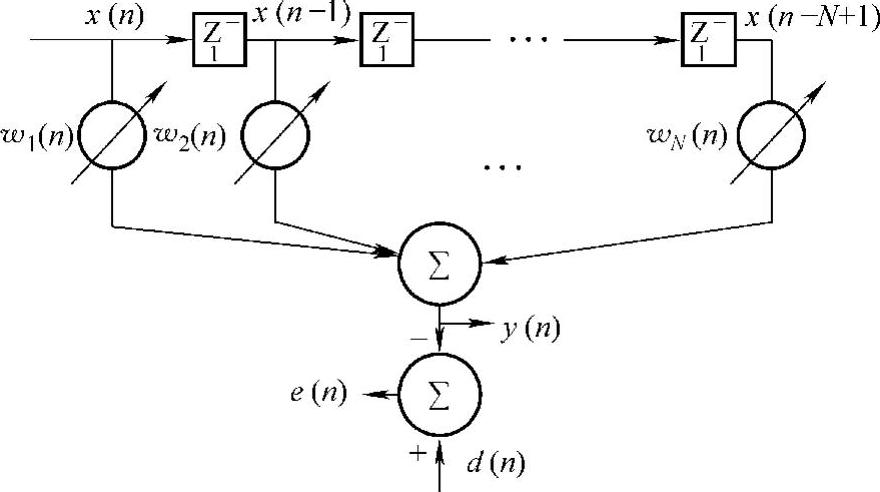
图9-4 用于联合参数估计的横式滤波结构

x（n）的自相关函数及与d（n）的互相关函数为

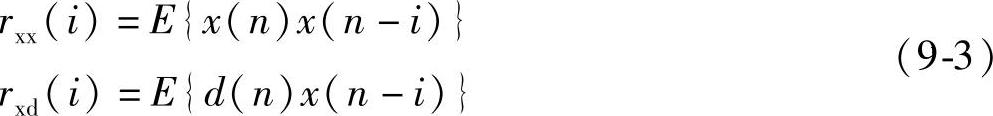
设加权矢量即滤波器系数矢量w=[w₁w₂…w_N]^T，滤波器在n时刻的输出为

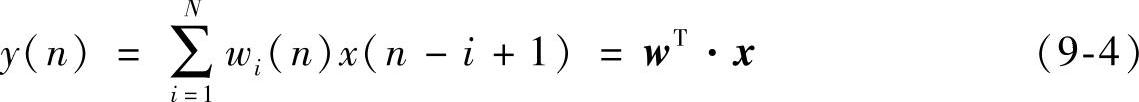
相应的误差为

e（n）=d（n）-y（n）=d（n）-w·x （9-5）

自适应滤波器控制机理是用误差序列e（n）按照某种准则和算法对其系数{w_i（n）}，（i=1，2，…，N）进行调节，最终使自适应滤波的目标（代价）函数最小化，达到最佳滤波状态。按照均方误差（MSE）准则所定义的目标函数是

F[e（n）]=ξ（n）=E[e²（n）]=E[d²（n）-2d（n）y（n）+y²（n）]（9-6）

将式（9-4）代入到式（9-6）中并整理得：

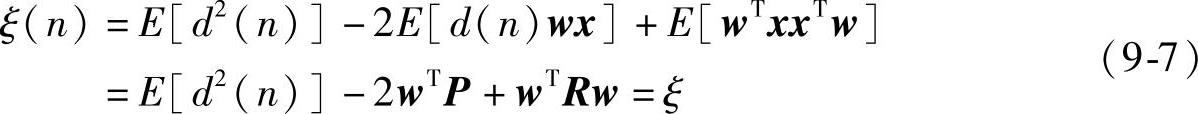
式（9-7）是均方误差性能函数，其中R是输入信号自相关矩阵。

P是输入信号x与期望d的互相关矢量，定义如下：

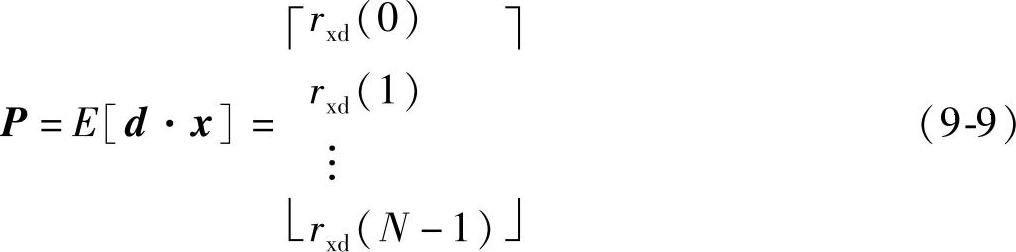
由式（9-7）可以看出，自适应滤波器的性能函数ξ（n）是w的二次函数，且矩阵R对称且非负定，因此ξ（n）有最小值。ξ（n）对w求梯度并使梯度等于零即可得到性能函数最小的最佳滤波系数为

w₀=R^-1P （9-10）

将上式结果代入到式（9-7）中并整理得到最小误差为

ξ_min=E{d²（n）}-w₀P （9-11）

当矩阵R和P已知时，可由式（9-10）直接求解，把此解称为维纳解即最佳滤波系数值。因为MSE函数是滤波系数w的二次方程，由此形成一个多维的超抛物曲面，这好像一个碗状曲面又具有唯一的碗底最小点，通常称之为自适应滤波器的误差性能曲面。当滤波器工作在平稳随机过程的环境下，这个误差性能曲面就具有固定边缘的恒定形状。自适应滤波系数的起始值{w_i（0）}（i=1，2，…，N）是任意值，位于误差性能曲面上的某一点。经过自适应调节过程，使对应于滤波系数变化的点朝碗底最小点方向移动，最终到达碗底最小点得以实现最佳维纳滤波。

最小均方滤波算法：高效的信号处理方法

相关推荐