同时,克里金插值能给出插值的误差,使插值的可靠程度一目了然。例如,对纽约市的交通事故数据进行克里金插值分析。最终得到的普通克里金插值结果如图3.20所示。从普通克里金插值结果中还能清晰地看出交通事故是沿城市的主要道路分布的。......
2025-09-29
对于一维有限长的N个点进行正交变换可得到N个变换域系数,若对此N个系数进行反正交变换即可完全恢复原N点信号。如果将反变换的时域序号用连续的时间代替,则即可在抽样点上恢复抽样信号,还可以获得其他时间点信号。由于不同的分段起点,可能存在N个不同的数据段都包含待插值的样点I(n),即将产生N个不同的插值结果,全相位插值就是取这N个插值的均值作为最终结果。
设有限长序列x(n),取其中任一长度为N的子序列X(n),正交变换α和反正正交变换β过程如下:
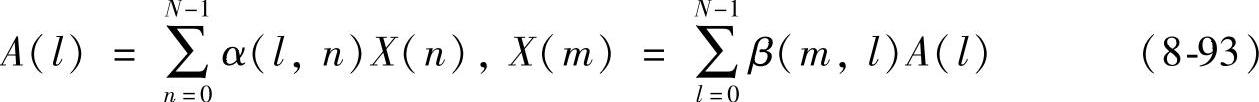
则连续的插值信号可由下式产生:
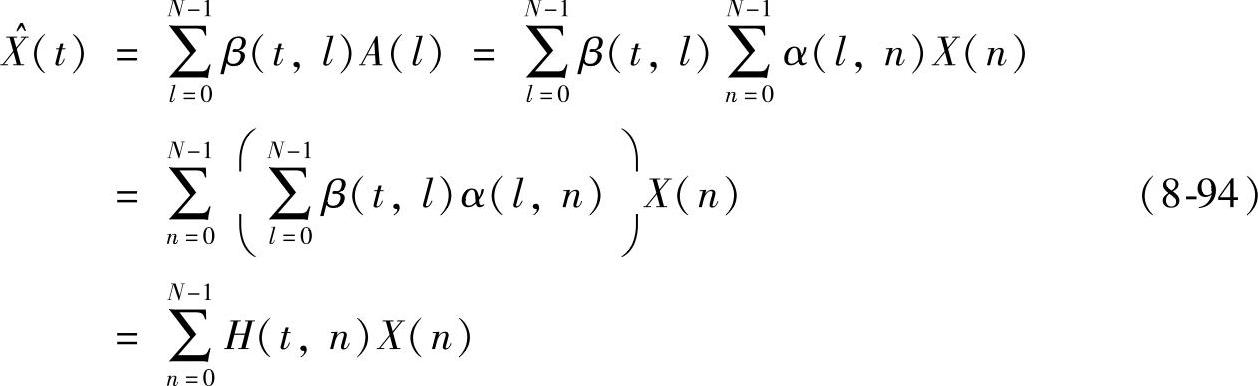
式中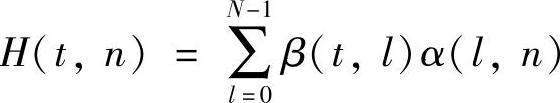
Walsh变换基只有±1离散值,傅里叶变换基有复数,因此选择DCT基作为插值的正交变换。正反变换定义如下:
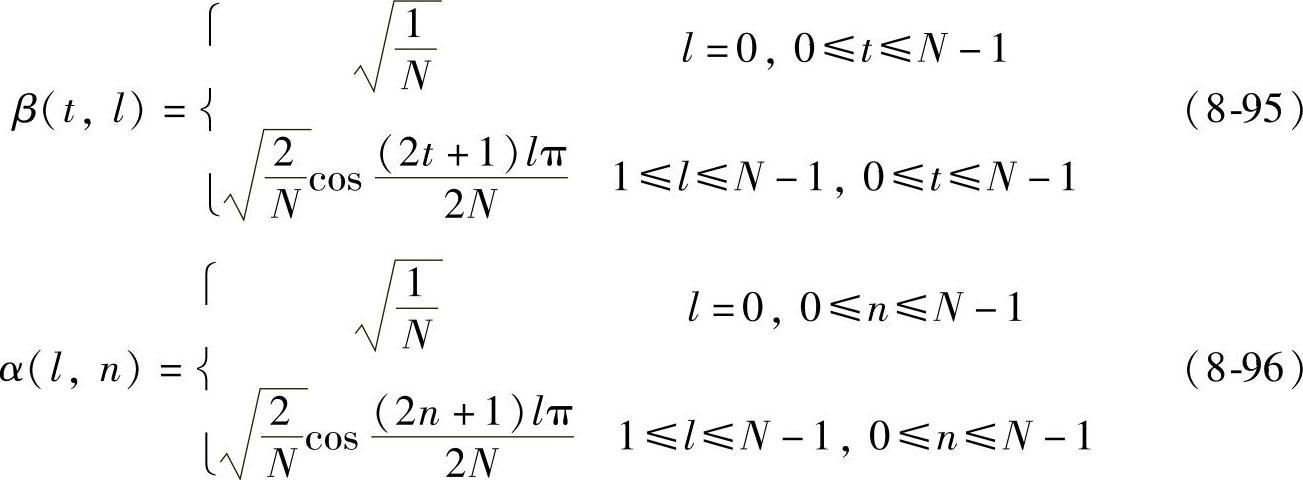
对于序列x中包含x(n)和x(n+1)的任意内插点x(n+τ)的分段共有N-1个,其中0≤τ<1,如图8-22所示。
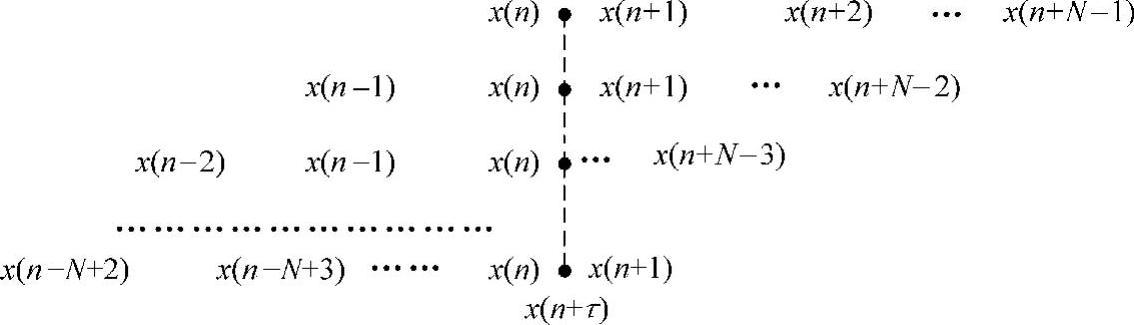
图8-22 包含内插点的N-1个数据段
每段生成的插值点结果为
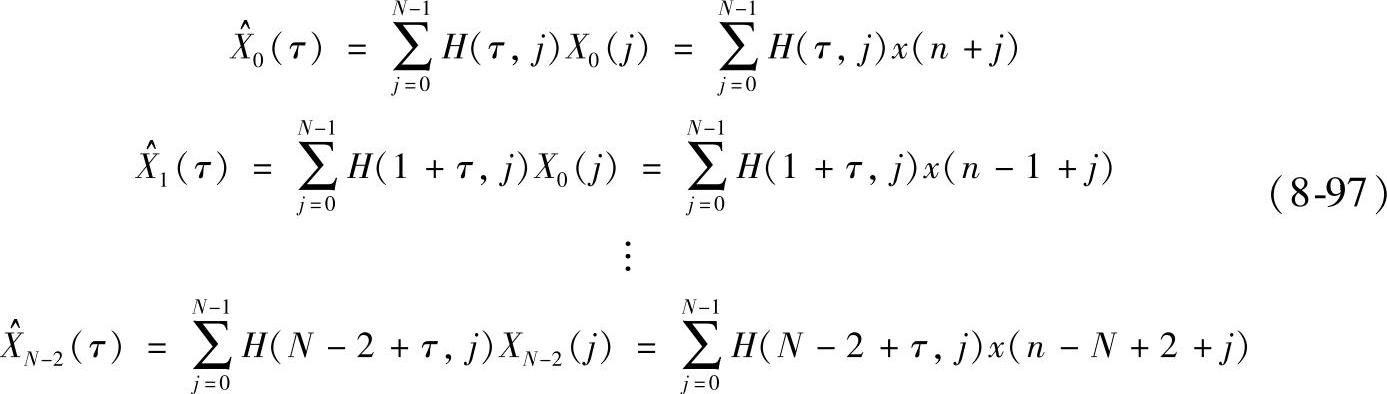
全相位内插是所有分段产生的内插结果和的平均值,即全相位内插值等于
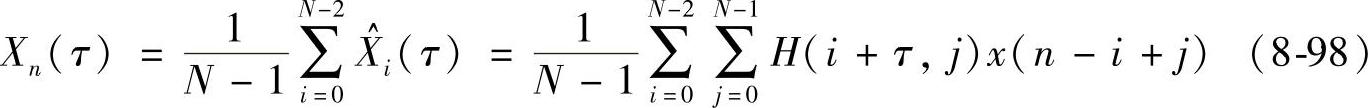
令k=i-j并交换求和顺序可得到:
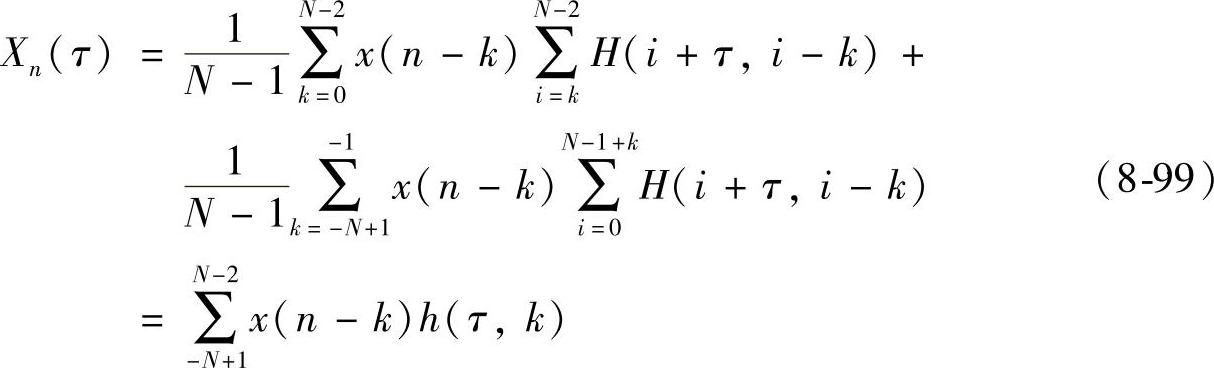
式中
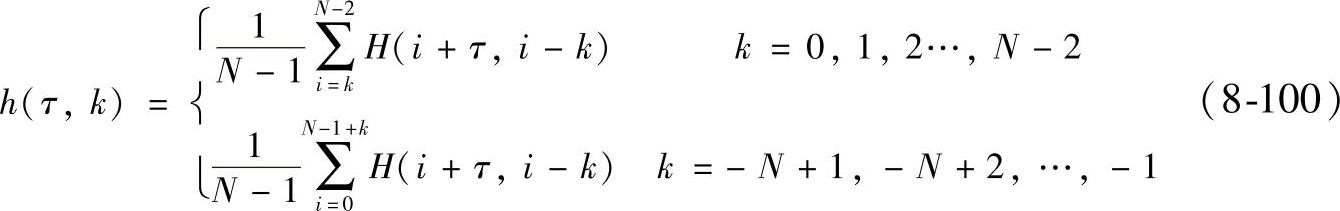 (https://www.chuimin.cn)
(https://www.chuimin.cn)
按照式(8-99)写出N=4时的六点内插公式如下:
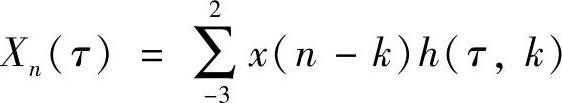
由式(8-100)可写出内插核分段函数如下:
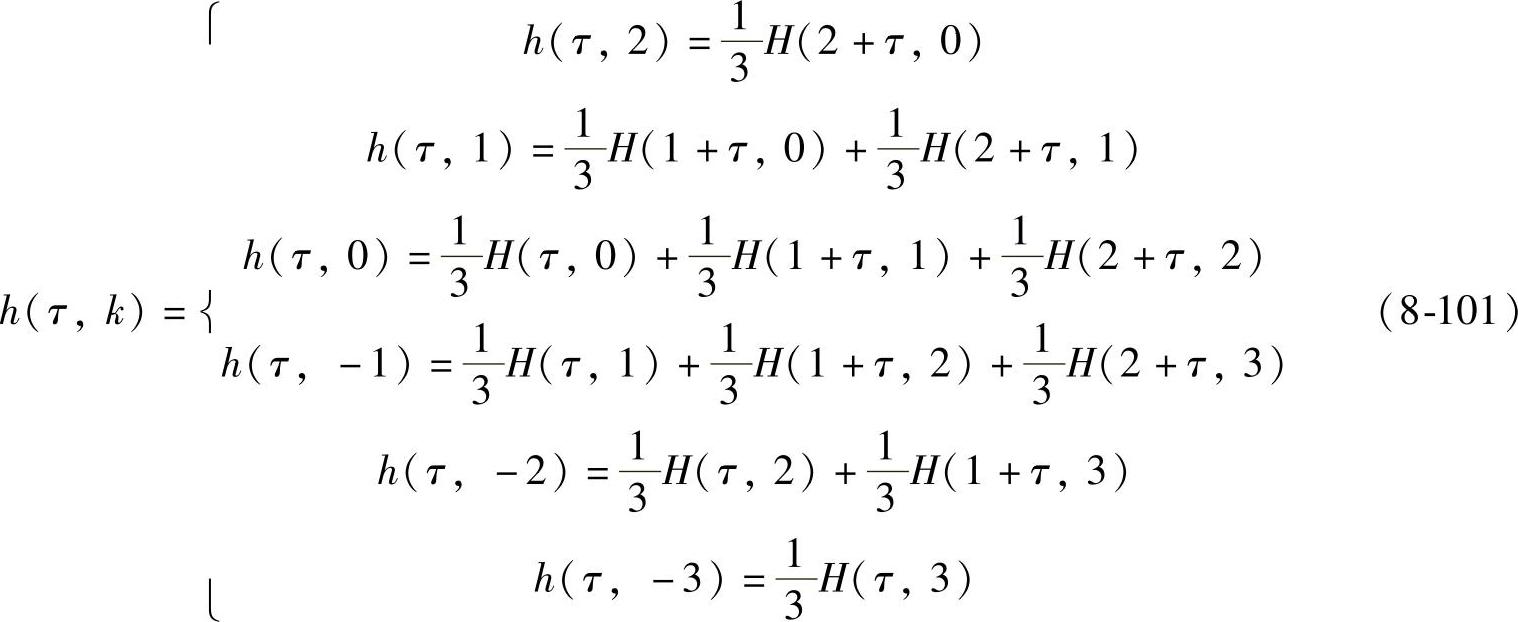
以x表示各数据段相对于插值点的距离,即x=k-τ,重写式(8-101)如下:
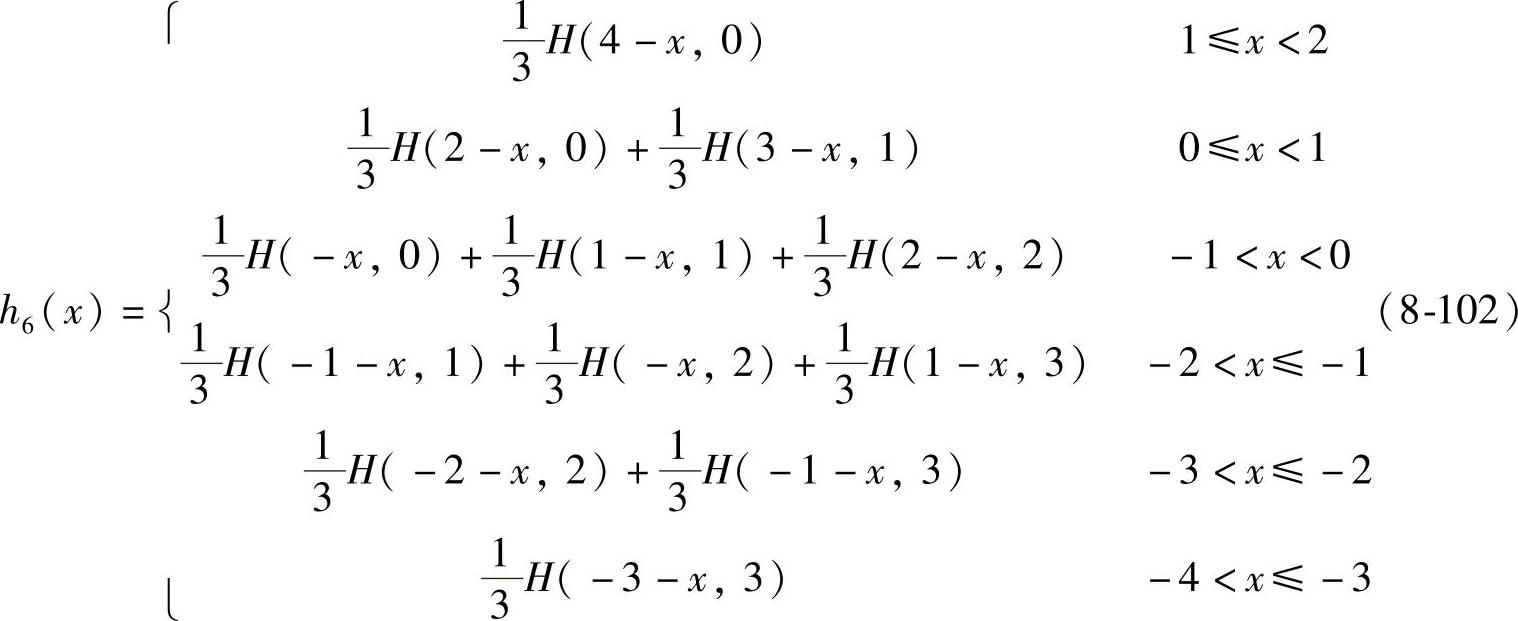
同理可写出N=5时的八点内插核分段函数为
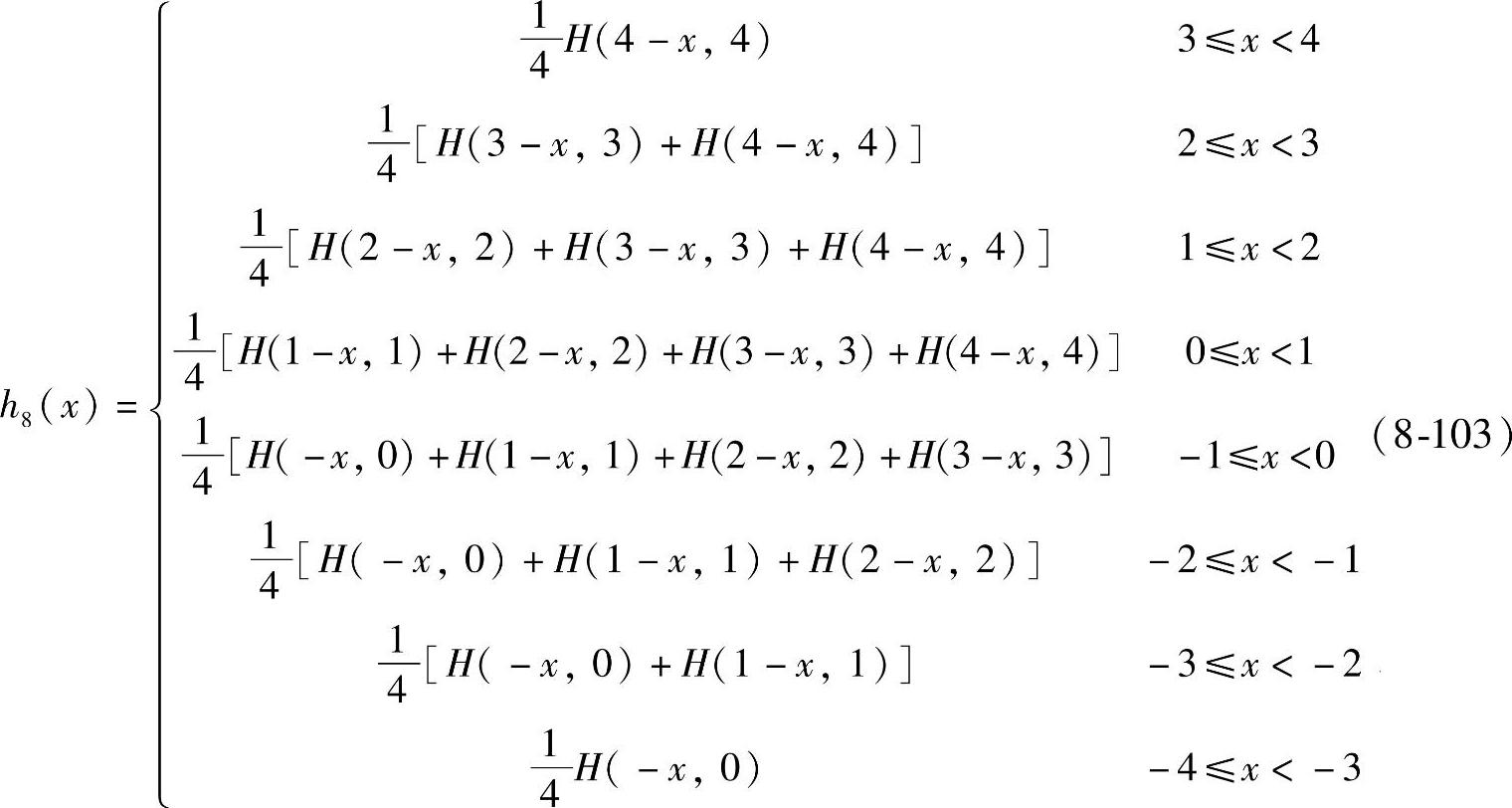
八点全相位内插核时频图如图8-23所示。
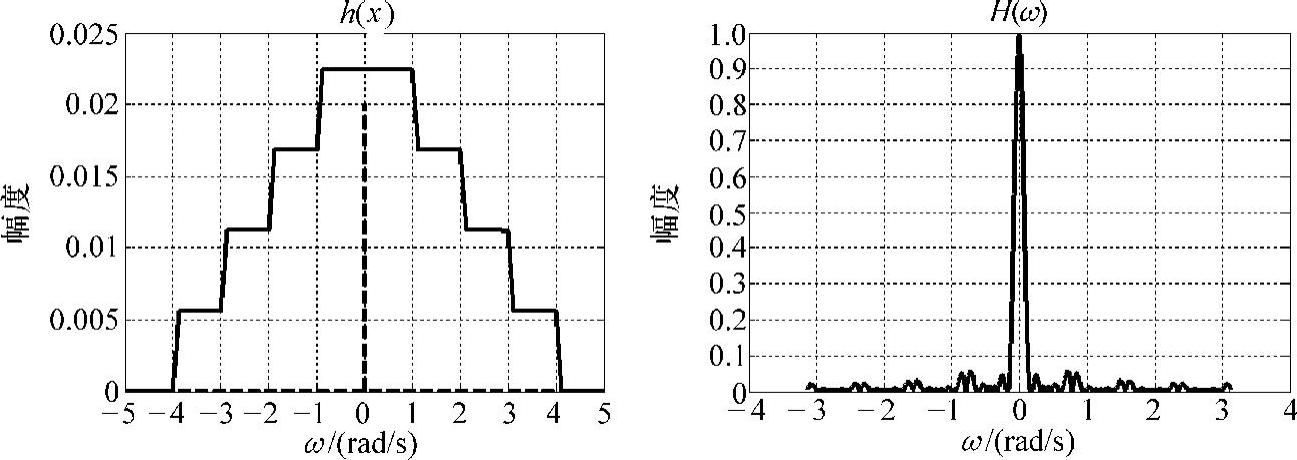
图8-23 八点全相位DCT内插核时频图(N=5)
对与上面实验中相同的Chirp信号进行插值重建,实验结果如图8-24所示。

图8-24 全相位Ⅰ型内插实验结果
实现上述结果的MATLAB代码[只列出h(x)生成函数]如下:


相关文章

同时,克里金插值能给出插值的误差,使插值的可靠程度一目了然。例如,对纽约市的交通事故数据进行克里金插值分析。最终得到的普通克里金插值结果如图3.20所示。从普通克里金插值结果中还能清晰地看出交通事故是沿城市的主要道路分布的。......
2025-09-29

系统原理同图2-26所示,对应的输出为式中式中Tk的表达式与apDCT时相同。此外,apDWT具有与apDCT相同的传输特性函数形式,因此也具有严格零相位的特性。图4-11 基于apDWT子带分解信号图实际上,不论是何种正交变换,按照全相位信号处理方法得到的ap都可以对信号进行去除分段效应的滤波和处理,它是建立在新概念上的一种滤波系统。......
2025-09-29

即N阶频域全相位滤波器与2N-1阶加三角窗的FIR滤波器等效,此FIR滤波器的单位冲击响应是全相位滤波器特性H的反离散傅里叶变换的两个周期延拓,第一等效图如图2-17所示。图2-17 N阶无窗全相位滤波器第一等效图以下MATLAB代码验证了图2-17与图2-15的DFT域全相位等效。......
2025-09-29

图4-12 变换域信号处理图对于N阶系统,时刻n输入xn=[x,x(n-1),…其中X1是1维N阶全相位输入信号,即式就是全相位数字信号处理得到的输出与输入的数学关系表达。把式称为全相位变换,矩阵A称为全相位变换基,矩阵T则为全相位变换核。综合以上,变换域全相位数字信号处理一种可能实现如图4-16所示。......
2025-09-29

在一维信号处理中,用来抑制噪声干扰并保留原有有用信号的滤波方法以及获得各种信号变换的数字滤波器,有着极其重要和广泛的应用。所以,统计结果表明二维图像信号谱能量90%以上集中在二维低频区域,如果进行2∶1或更高亚取样,谱也未发生重叠。为了克服边缘效应,一种有效的方法是对图像进行重叠滤波,在重叠滤波中的子图像在行列方向上逐点进行重叠。......
2025-09-29

分析建筑全生命周期的物质循环过程,可以研究影响整个循环系统物质流的主要因素。建筑生命周期循环系统,是建筑生命周期内各个阶段与自然界构成的一个大系统。建筑生命周期物质循环系统的平衡程度反映了清洁生产的实施绩效。因此,建筑全生命周期的生态平衡系数,是清洁生产的关键评价指标。......
2025-09-29

国际标准建议CCITT H.261、JPEG、MPEG中都采用8×8的块做DCT,但基于DCT的数字滤波尚不普遍。为使DCT所具有的优良特性能在数字滤波中得到充分发挥,结合全相滤波的概念提出了DCT域ap系统设计。TN-2TN-1],其传输特性为显然,apDCT具有严格零相位。实现无窗、单窗和双窗apDCT与传统滤波器特性的MATLAB代码如下:显然,apDCT具有严格零相位。利用apDCT的各子带滤波器对图像的一行进行子带滤波的结果如图4-8所示。......
2025-09-29

20世纪70年代初,滤波器组首先在语音编码和多路复用中得到了应用。所谓滤波器组就是将信号按不同的频带分解成一组信号,并将分解得到的子带信号重新合成原信号的处理系统。80年代后期,M.J.Smith等人提出了运用谱分解法设计无失真地重建原始信号的滤波器方法,但存在相位失真。......
2025-09-29
相关推荐