首页理论教育沃尔什内插模板简介

沃尔什内插模板简介

2025-09-29 理论教育版权反馈

【摘要】：显然，采用这种重叠滤波器内插就可以消除高列率谱的混叠。模板与图像做尺寸为3×3的卷积即得重叠滤波的全部输出，其结果与全部2×2子图像逐行逐点移动作低通滤波器后的叠加输出平均相同。显然，这就是我们在第5章中设计的二维全相位滤波器或称全相位内插模板。全相位沃尔什内插模板的设计就是给定低通滤波器H求出模板T的过程。

按照4×4分割的子图像窗口在行列方向上移动产生相互重叠的其他位置子图像，与其中某像素P有关的共有16个，遍及在原始图像中7×7像素的范围内。

如图8-3所示，图中没有把与像素P相关的16个子图全部画出，只列出了4个子图像。对与像素P相关即包含其在内的16个子图像经过二维低通滤波器处理后的输出值平均值（这种平均可以是加权平均）即为重叠滤波器的输出。显然，采用这种重叠滤波器内插就可以消除高列率谱的混叠。如图8-3所示，对于1/2取样图像，相邻的子图像反复出现h₁和h₂结构，这两种结构的高列率分量幅度近似相等而相位相反，所以在重叠相加时基本上对消，从而有效地克服了按子图分块滤波恢复拼接时的边缘效应。

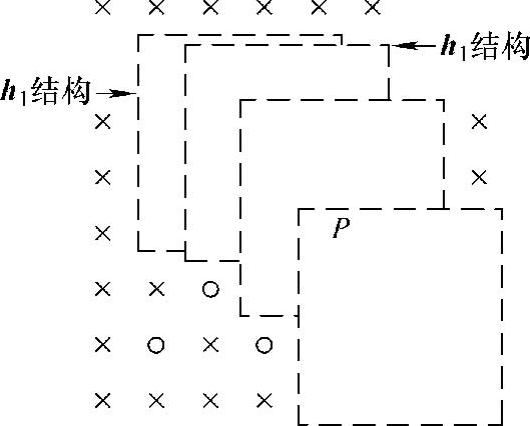
图8-3 4×4子图像重叠滤波的构成

下面讨论最简单的子图像为2×2的二维低通重叠滤波器。如图8-4所示，与像素a₅相关的图像共有4个子块X_i，其包含的像素分别为[a_i，a_i+1；a_i+3，a_i+4]（i=1，2，4，5）。

图8-4 对应2阶低通列率滤波器的3阶重叠模板构造

某个2×2的子图像a经过二维沃尔什变换后为

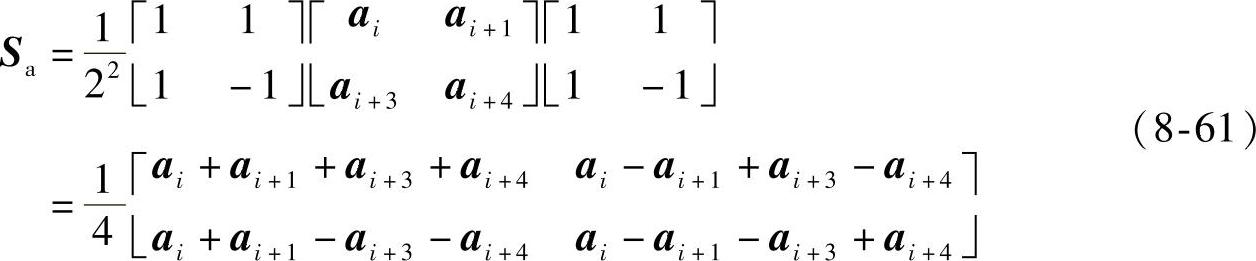
经过滤波器H₂后变为

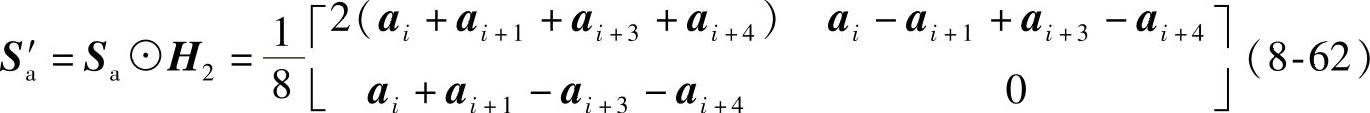
再经过二维沃尔什反变换得到内插恢复的子图像a′如下：

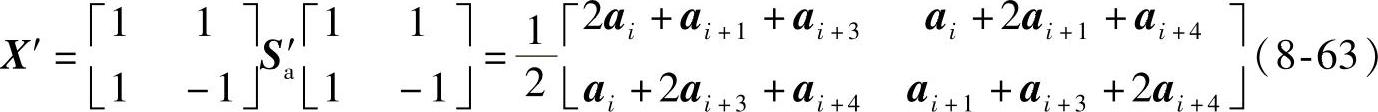
当i=1～4，对应点a₅的输出分别如下：

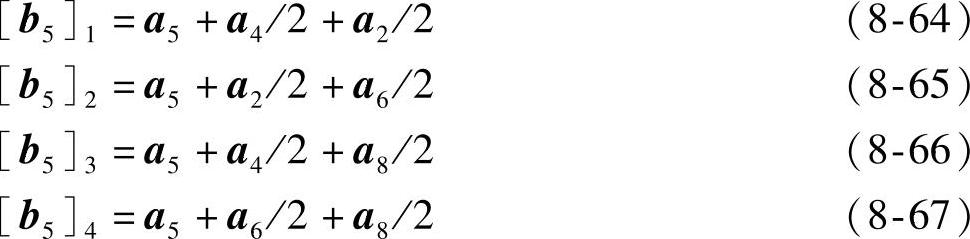
上面4个表达式（8-64）～式（8-67）的输出和的平均就是重叠滤波器输出b₅，即

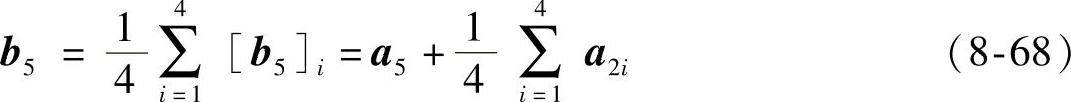
式（8-68）可用一个模板来表示为(https://www.chuimin.cn)

模板与图像做尺寸为3×3的卷积即得重叠滤波的全部输出，其结果与全部2×2子图像逐行逐点移动作低通滤波器后的叠加输出平均相同。这种基于模板的内插方法计算简单，对于1/2抽取后保留的像素内插后处理不变，对于内插产生的新像素值等于周围4个像素的平均值。

以上分析的子图像尺寸是2×2，当图像尺寸为N×N时，与某样点相关的子图像有N²个，它们分别滤波后并进行叠加的平均输出，可以表示成一个尺寸大小为（2N-1）×（2N-1）的模板，这个模板与图像的逐点卷积即得重叠滤波的全部输出。显然，这就是我们在第5章中设计的二维全相位滤波器或称全相位内插模板。

全相位沃尔什内插模板的设计就是给定低通滤波器H求出模板T的过程。以一维N阶沃尔什变换域列率滤波器为例，若输入数据为x（n），列率滤波器的变换域特性为H（k），滤波后输出应为x与h的并元卷积。每一子段经过H滤波的输出重叠过程如图8-5所示。

图8-54 阶并元移位及重叠

由图8-5重叠输出结果可以看出，一维全相位内插模板可以表示成矩阵Q与h相乘的形式：

式（8-70）中，W是沃尔什基矩阵；Q是并元移位叠加矩阵，定义如下：

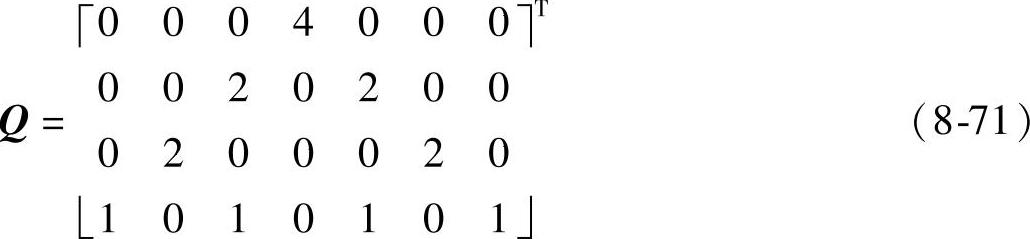
总结以上，对于N阶二维沃尔什全相位滤波，从传输矩阵H求出模板T的过程如下：

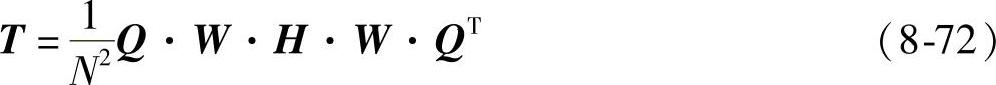
式中，W是N阶沃尔什基矩阵；Q是N×（2N-1）并元移位叠加矩阵，定义如下：

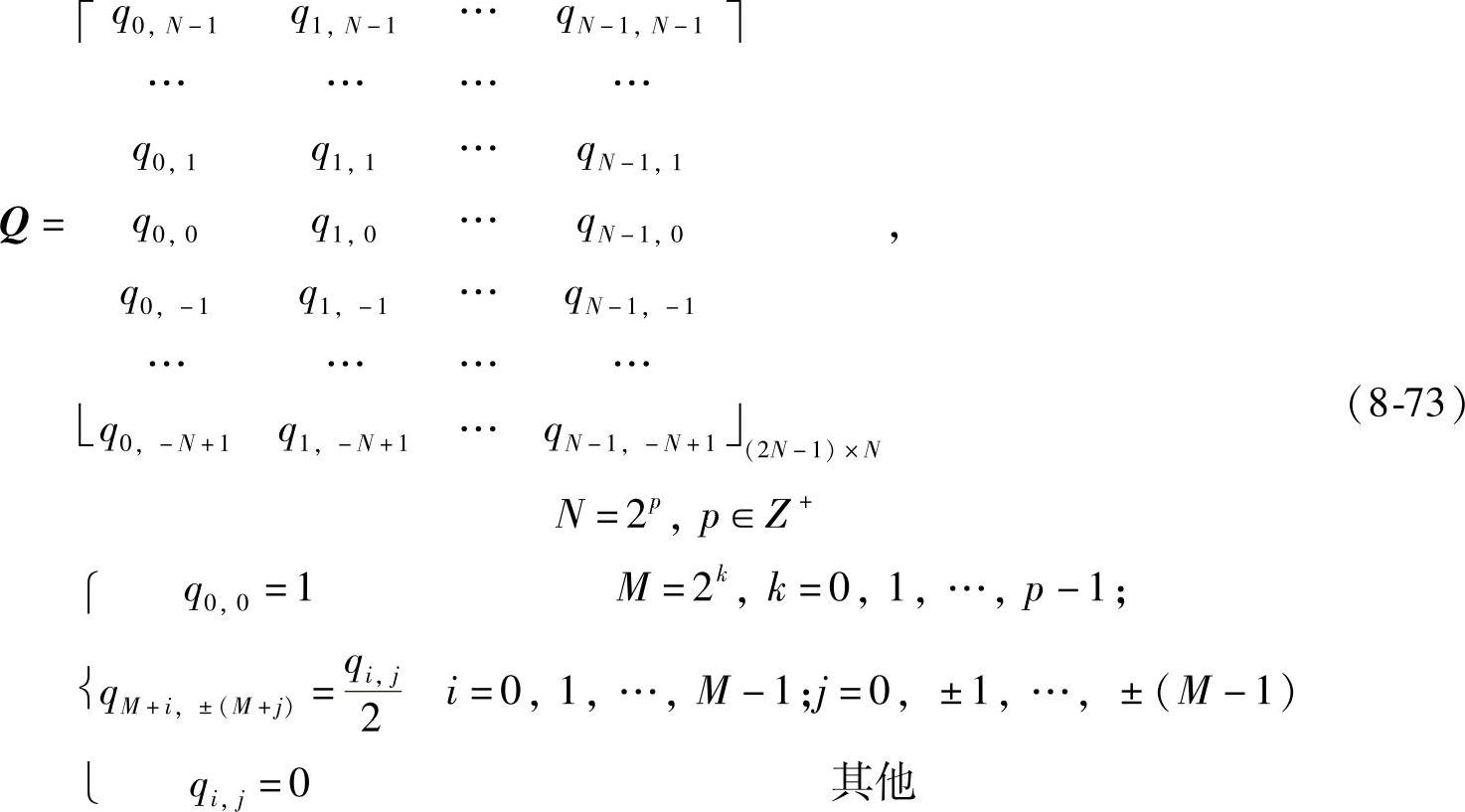
根据式（8-72），如果已知模板T，可通过下式求其对应的传输矩阵H：

H=W·Q·T·（Q）T·W （8-74）

式中，Q是并元移位叠加矩阵Q的伪逆。