首页 理论教育基于二维傅里叶变换的内插模板优化技术

基于二维傅里叶变换的内插模板优化技术

2023-06-23 理论教育 版权反馈
【摘要】：正交基为傅里叶算子时，模板设计过程与上面沃尔什算子基本相同，不同之处在于卷积类型变为循环卷积。傅里叶基设计的特点是可以构造任何大小的内插模板，而不限于2的整数次幂。

正交基为傅里叶算子时，模板设计过程与上面沃尔什算子基本相同，不同之处在于卷积类型变为循环卷积。傅里叶基设计的特点是可以构造任何大小的内插模板，而不限于2的整数次幂。下面抽取算子除了1/3外，均同沃尔什变换相同。

1.1/2内插模板

1）维度等于2时的1/2抽取方式，调制点D1/2等于d1/2的二维傅里叶变换，求出H1/2的通解如下：

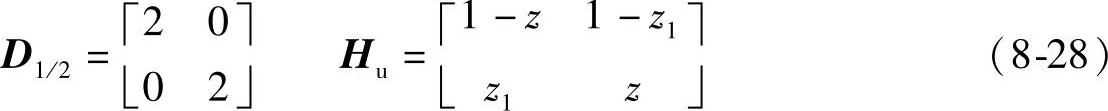
978-7-111-48233-8-Chapter08-28.jpg

与Walsh正交基变换相同，定制如下滤波器，其反变换即为非重叠模板T1/2。

978-7-111-48233-8-Chapter08-29.jpg

2）维度等于4时的1/2抽取方式，调制点矩阵D1/4和滤波器H1/4通解如下：

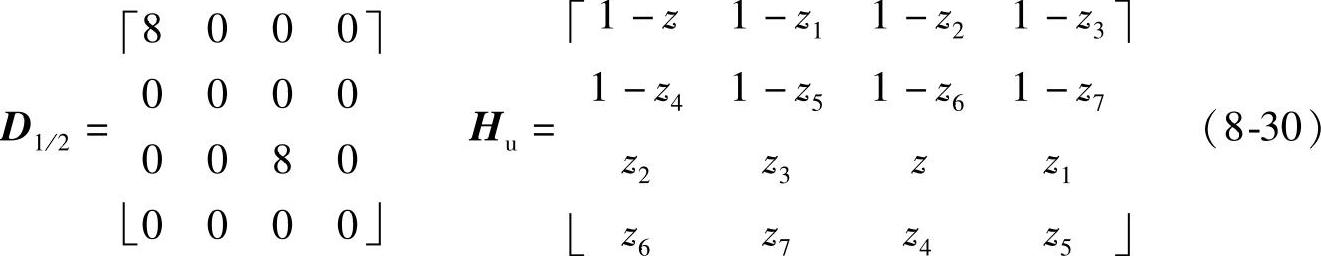
978-7-111-48233-8-Chapter08-30.jpg

定制如下滤波器，其反变换即为非重叠模板T1/2。

978-7-111-48233-8-Chapter08-31.jpg

2.1/3内插模板

如图8-1f中1/3抽取方式的抽取算子d1/3及对应的调制点矩阵D1/3如下：

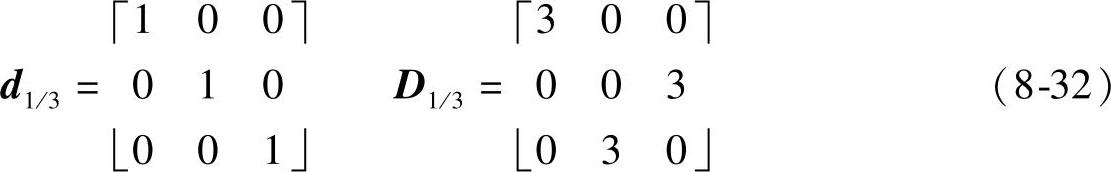
978-7-111-48233-8-Chapter08-32.jpg

求出H1/3的通解如下：

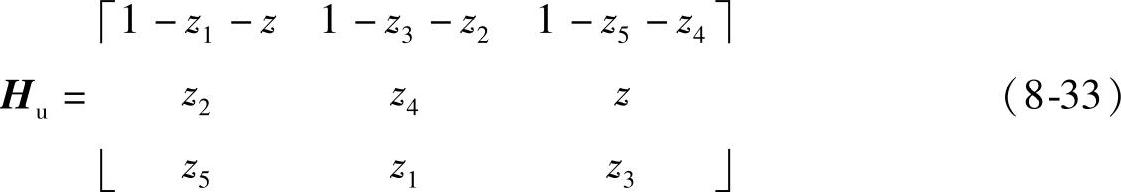
978-7-111-48233-8-Chapter08-33.jpg

定制如下滤波器，其反变换即为非重叠模板T1/3。

978-7-111-48233-8-Chapter08-34.jpg

3.1/4内插模板

1）图8-1b对应的调制点D1/4及H1/4的通解如下：

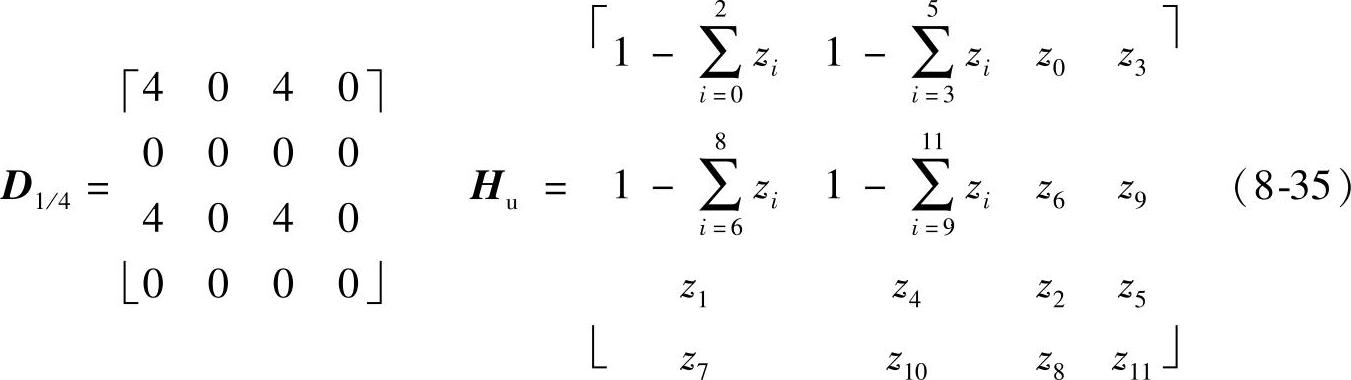
978-7-111-48233-8-Chapter08-35.jpg

定制如下滤波器，其反变换即为非重叠模板T1/4。

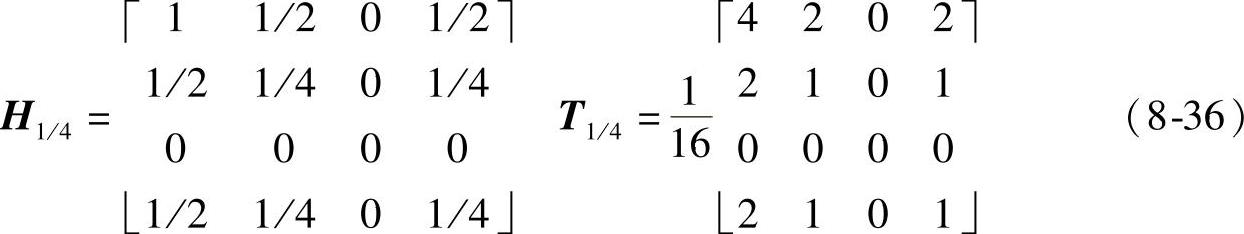
978-7-111-48233-8-Chapter08-36.jpg

2）图8-1c对应的调制点D1/4及H1/4的通解如下：

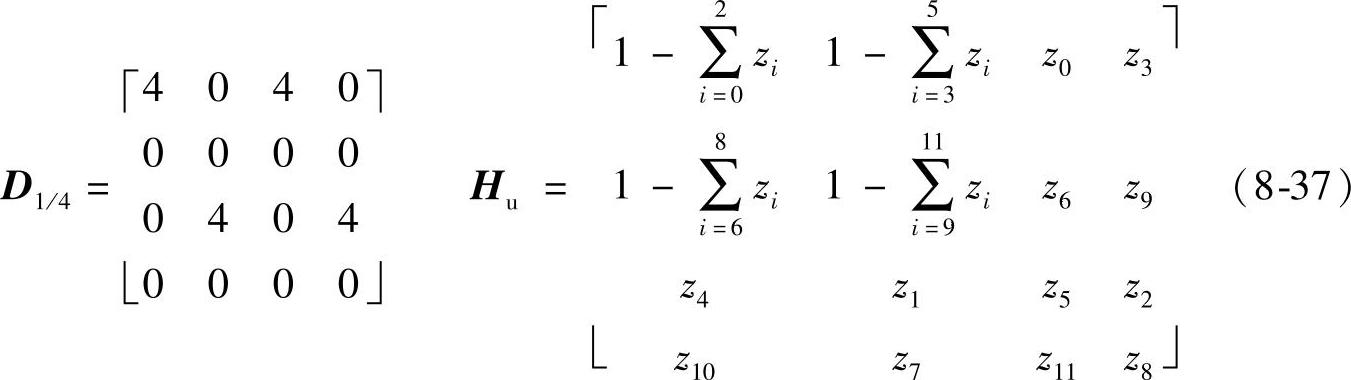
978-7-111-48233-8-Chapter08-37.jpg

定制如下滤波器，其反变换即为非重叠模板T1/4。

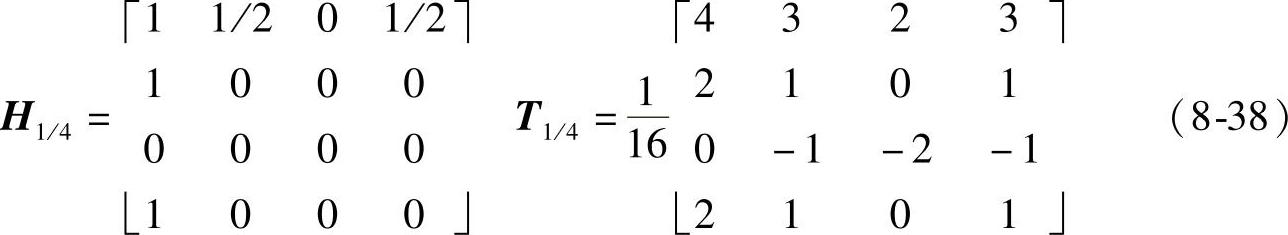
978-7-111-48233-8-Chapter08-38.jpg

4.1/8内插模板

1）图8-1d对应的调制点D1/8及H1/8的通解如下：

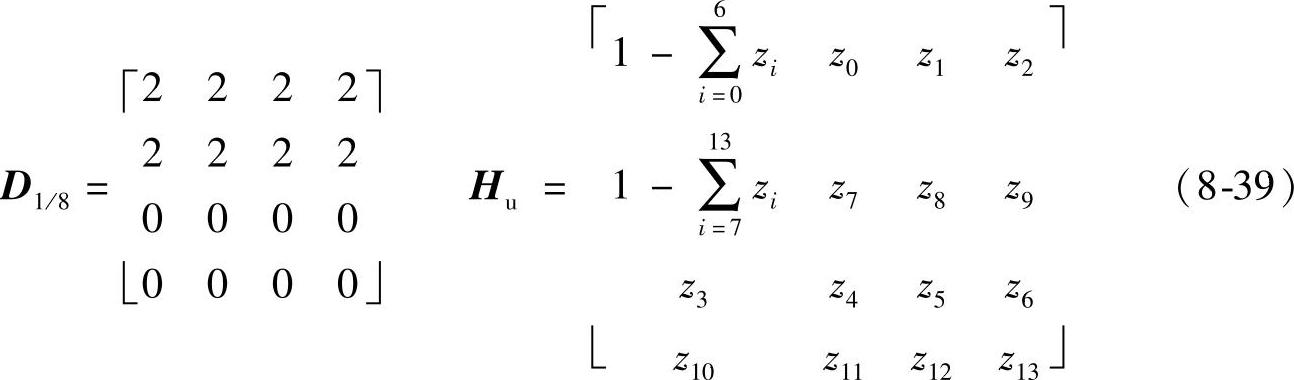
978-7-111-48233-8-Chapter08-39.jpg

定制如下滤波器，其反变换即为非重叠模板T1/8。

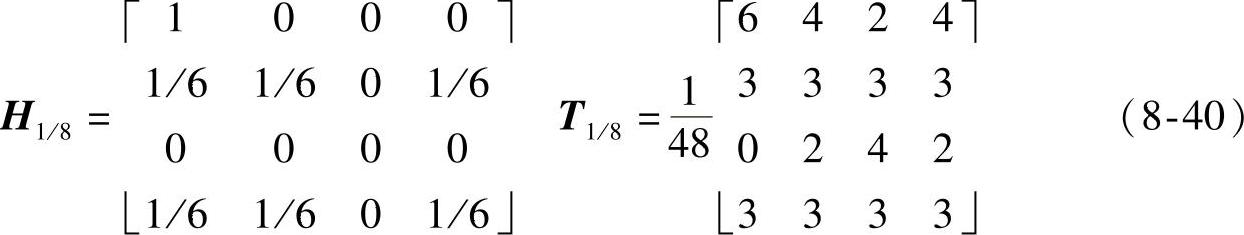
978-7-111-48233-8-Chapter08-40.jpg

2）图8-1e对应的调制点D1/8及H1/8的通解如下：

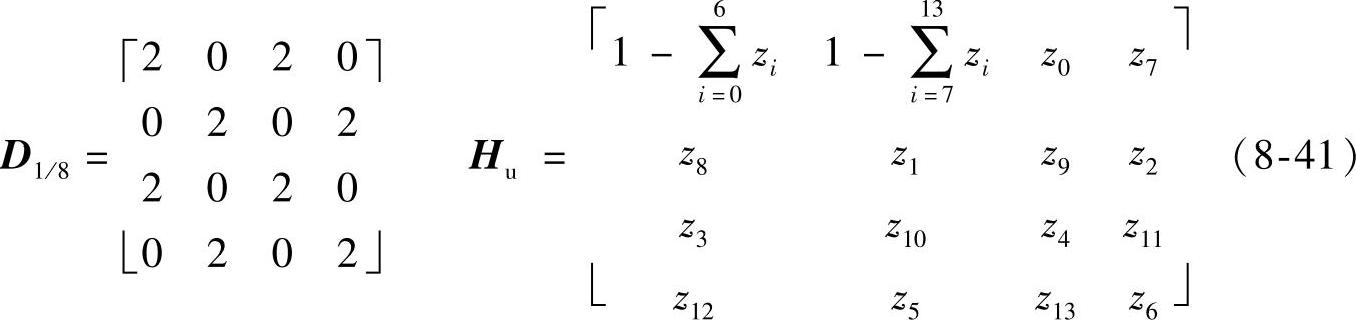
978-7-111-48233-8-Chapter08-41.jpg

定制如下滤波器，其反变换即为非重叠模板T1/8。

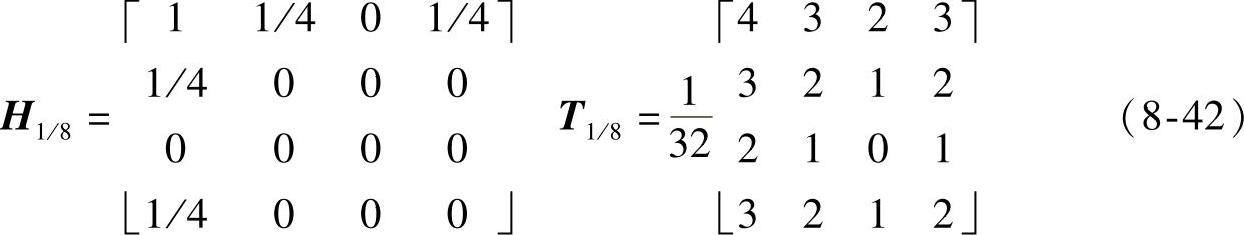
978-7-111-48233-8-Chapter08-42.jpg

有关全相位数字信号处理方法及MATLAB实现的文章

  • 基于二维DCT变换的内插模板技术 基于二维DCT变换的内插模板技术

    由第5章内容可知，二维DCT运算可以转化成DFT运算，然后取结果的实部作为DCT变换的结果。DCT基可以设计任何大小的内插模板，而不限于2的整数次幂。以上面傅里叶基构造的结果直接得到DCT基滤波器H和对应的非重叠模板。图8-1c对应的定制H1/3如下，其反变换即为非重叠模板T1/3。......

    2023-06-23

    详细阅读
  • 基于二维沃尔什变换的内插模板优化 基于二维沃尔什变换的内插模板优化

    这种类型的算子可以定义为4阶，相应的抽取算子d1/8和调制点矩阵D1/8如下：3.1/8内插模板1）第一种类型。......

    2023-06-23

    详细阅读
  • 基于形状模板的匹配算法提升视觉测量技术 基于形状模板的匹配算法提升视觉测量技术

    1988年kass等人提出的基于能量函数的活动轮廓模型，即Snake模型，便是一种典型的自由式变形模板模型。Snake模型是一种有效地寻找目标轮廓的搜索算法，具有良好的提取、跟踪特定区域内目标边缘的能力，工作过程主要是利用能量最小化原理。实现Snake模型原型的算法通常十分复杂，曲线收敛速度慢且搜索范围有一定限制，因此许多学者提出了不同的算法，对经典Snake模型进行了改进。......

    2023-11-24

    详细阅读
  • 沃尔什内插模板简介 沃尔什内插模板简介

    显然，采用这种重叠滤波器内插就可以消除高列率谱的混叠。模板与图像做尺寸为3×3的卷积即得重叠滤波的全部输出，其结果与全部2×2子图像逐行逐点移动作低通滤波器后的叠加输出平均相同。显然，这就是我们在第5章中设计的二维全相位滤波器或称全相位内插模板。全相位沃尔什内插模板的设计就是给定低通滤波器H求出模板T的过程。......

    2023-06-23

    详细阅读
  • 二维傅里叶变换原理及应用 二维傅里叶变换原理及应用

    由式容易推导出傅里叶变换基矩阵如下：这里假设图像由N×N个元素组成。表5-14 阶傅里叶基本图像指数由式可得到傅里叶基本图像见表5-1。需要指出的是，傅里叶基本图像都是复图像。图5-34 阶傅里叶基本图像由图5-3可以看出，实部和虚部相位差是π/2，对于4阶傅里叶变换的空间单位频率是2π/4，即实部和虚部按隔行或隔列对准。......

    2023-06-23

    详细阅读
  • 二维离散傅里叶变换的性质及应用 二维离散傅里叶变换的性质及应用

    二维离散傅里叶变换有多种性质，这里仅介绍三种：可分离性、可计算性及移位性。图3.9 由2步一维离散傅里叶变换计算二维离散傅里叶变换移位性通常在二维离散傅里叶变换之前，将输入图像乘以（-1）x+y。它是二维离散傅里叶变换设置的M×N区域的中心。当在计算机中使用二维离散傅里叶变换时，总和的范围为（u=0，…......

    2023-11-24

    详细阅读
  • 基于内容的新闻推荐技术优化 基于内容的新闻推荐技术优化

    目前比较主流的推荐算法有基于协同过滤的推荐和基于内容的推荐等。由于协同过滤是根据用户对新闻的访问记录来进行推荐的，只有被阅读过的新闻才能被推荐，然而新闻的生命周期十分短暂，用户的访问矩阵会相当稀疏，这对于时效性要求比较高的新闻推荐系统是相当严重的缺陷，所以更多采用基于内容的推荐。大多数的基于内容的推荐系统在处理文字类item特征时，都会尝试将一篇文章映射到量空间模型。......

    2023-06-28

    详细阅读
  • 基于模板匹配的检索方法的介绍 基于模板匹配的检索方法的介绍

    这一模型意味着在我们的知识基础中，已经存储了数以百万计的不同模板——每一个可以辨识的不同物体或模式，都有一个与之匹配的模板存在。本书结合局部特征的特点和模板匹配的原理，提出了一种图像检索方法。如果局部特征和模板匹配的数量越多，则该幅图像和查询图相似的程度就越高。显然，模板匹配并不完全适合知觉原理的实际应用。......

    2023-06-28

    详细阅读