显然，采用这种重叠滤波器内插就可以消除高列率谱的混叠。模板与图像做尺寸为3×3的卷积即得重叠滤波的全部输出，其结果与全部2×2子图像逐行逐点移动作低通滤波器后的叠加输出平均相同。显然，这就是我们在第5章中设计的二维全相位滤波器或称全相位内插模板。全相位沃尔什内插模板的设计就是给定低通滤波器H求出模板T的过程。......
2023-06-23
基于二维沃尔什变换的内插模板优化
【摘要】：这种类型的算子可以定义为4阶，相应的抽取算子d1/8和调制点矩阵D1/8如下：3.1/8内插模板1）第一种类型。
模板的设计与抽取算子维度大小有关，1/2抽取算子维度定义为2×2和4×4两种以作对比，更高维度的推导过程与此基本相同。
1.1/2内插模板
1）维度等于2时的1/2抽取方式，其对应的抽取算子d1/2和调制点矩阵D1/2（其中D1/2等于d1/2的二维沃尔什变换）如下：
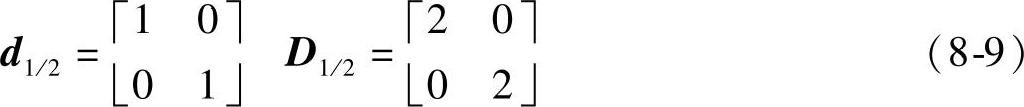
为满足式（8-7）和式（8-8）的要求，求出H1/2的通解如下：
按照通式来设计模板时需要考虑的几点有：首先，如果没有行和列上的高低频分布的先验信息，H在行列上应对称设置；其次，从上面模板设计过程可知H应为低通滤波器，所以选择H（0，0）=1且副对角线以下应全部为0。因此，可以实现的较合适的滤波器（其反变换即为非重叠模板T1/2）如下：
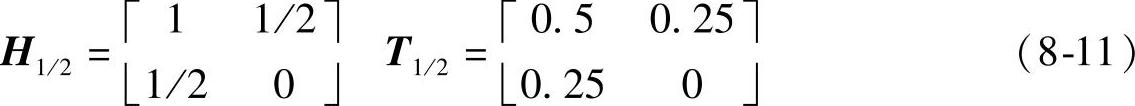
2）维度等于4时的1/2抽取方式，其对应的抽取算子d1/2和调制点矩阵D1/2（其中D1/2等于d1/2的二维沃尔什变换）如下：
求出H1/2的通解如下：
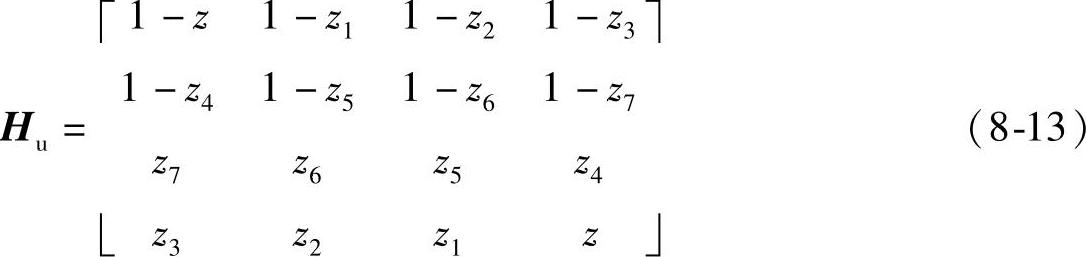
按上面选定基准定制滤波器H1/2（其反变换即为非重叠模板T1/2）如下：
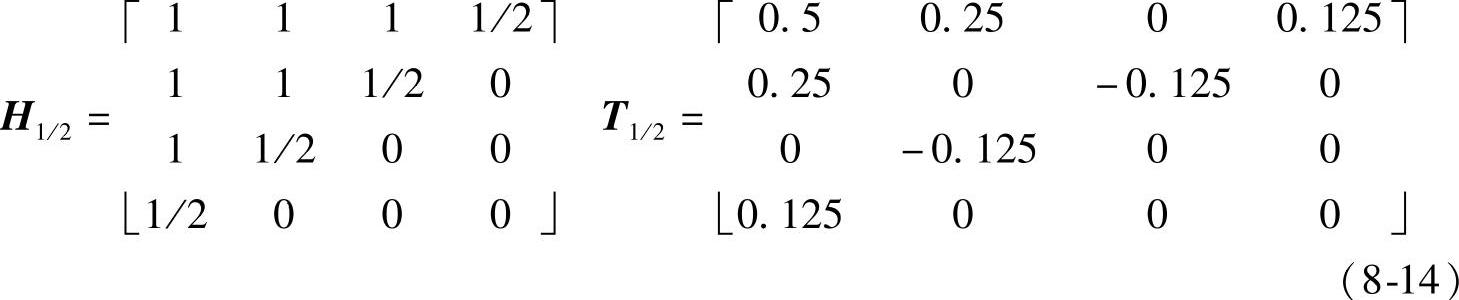
比较式（8-11）和式（8-14）可以看出，相同抽取系数K定义的不同维数抽取算子d具有膨胀特性，即4维的抽取算子d1/24可通过膨胀d1/22生成，如下所示：
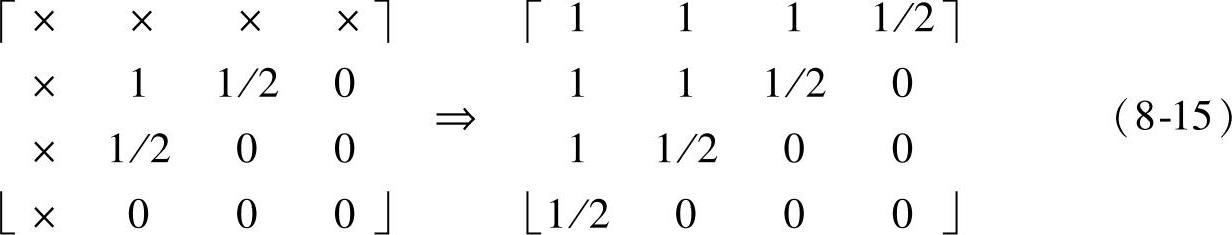
2.1/4内插模板
1）第一种类型（对应图8-1b），抽取算子d1/4和调制点矩阵D1/4（其中D1/4等于d1/4的二维沃尔什变换）如下：
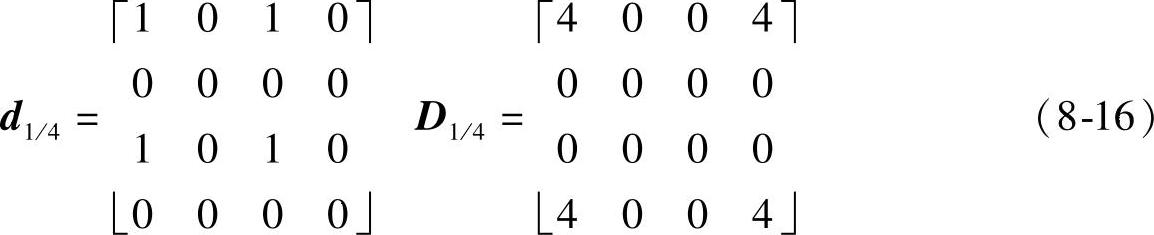
求出H1/4的通解如下：
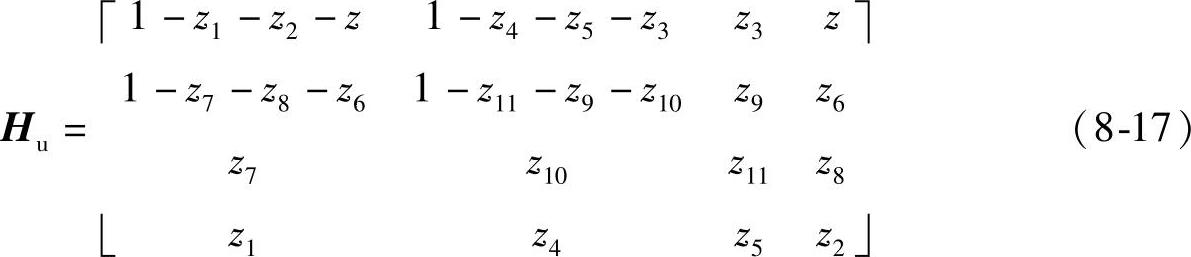
按上面选定基准定制滤波器H1/4（其反变换即为非重叠模板T1/4）如下：
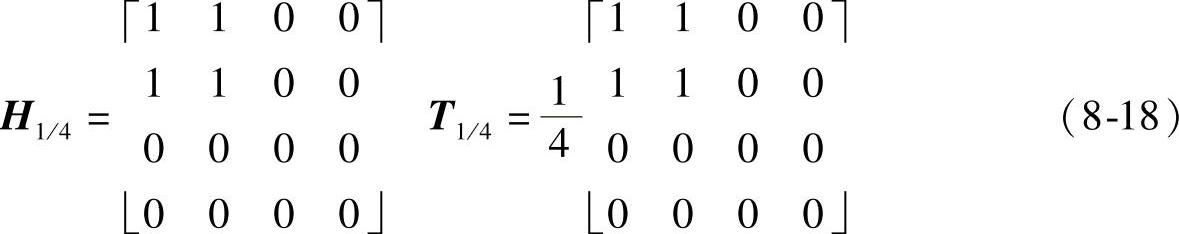
2）第二种类型（对应图8-1c），抽取算子d1/4和调制点矩阵D1/4（其中D1/4等于d1/4的二维沃尔什变换）如下：
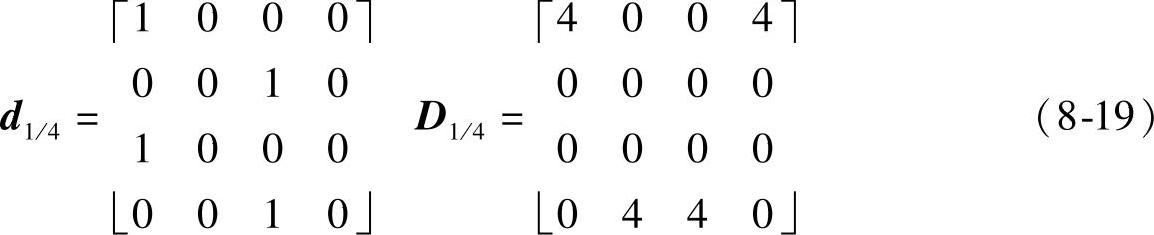
求出H1/4的通解如下：
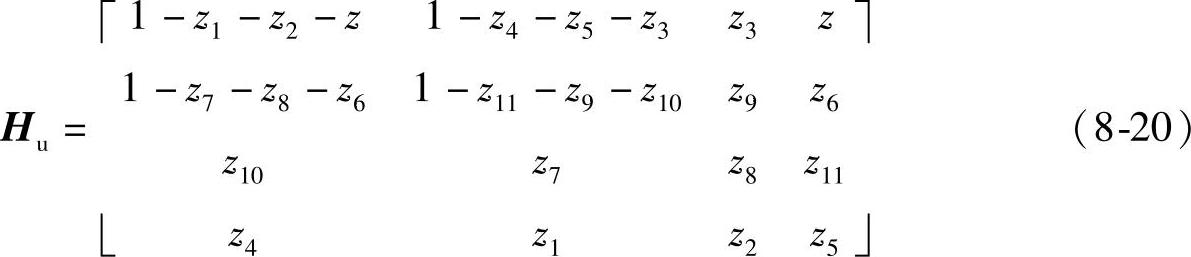
定制滤波器H1/4（其反变换即为非重叠模板T1/4）如下：
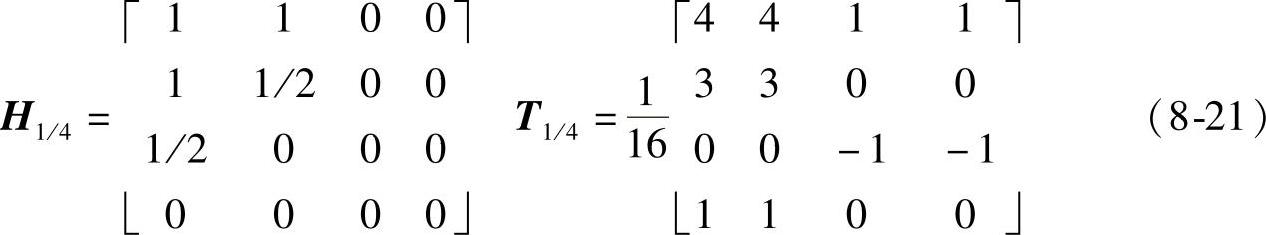
3.1/8内插模板
1）第一种类型（对应图8-1b）。这种类型的算子可以定义为4阶，相应的抽取算子d1/8和调制点矩阵D1/8（其中D1/8等于d1/8的二维沃尔什变换）如下：
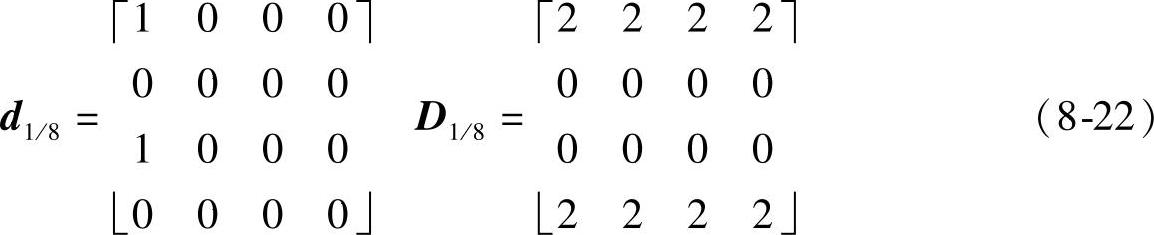
求出H1/8的通解如下：
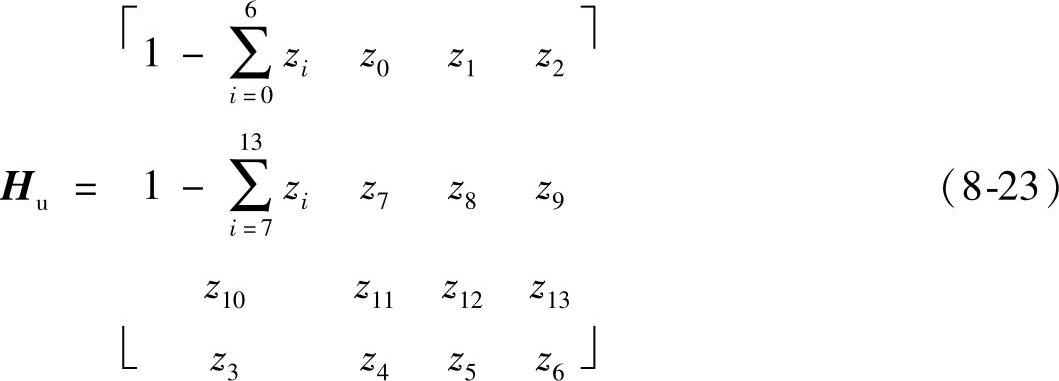
定制滤波器H1/8（其反变换即为非重叠模板T1/8）如下：
2）第二种类型（对应图8-1e）。这种类型的算子可以定义为4阶，相应的抽取算子d1/8和调制点矩阵D1/8（其中D1/8等于d1/8的二维沃尔什变换）如下：
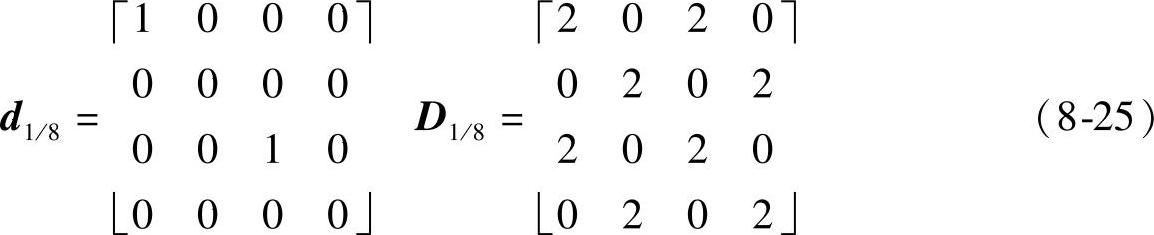
求出H1/8的通解如下：
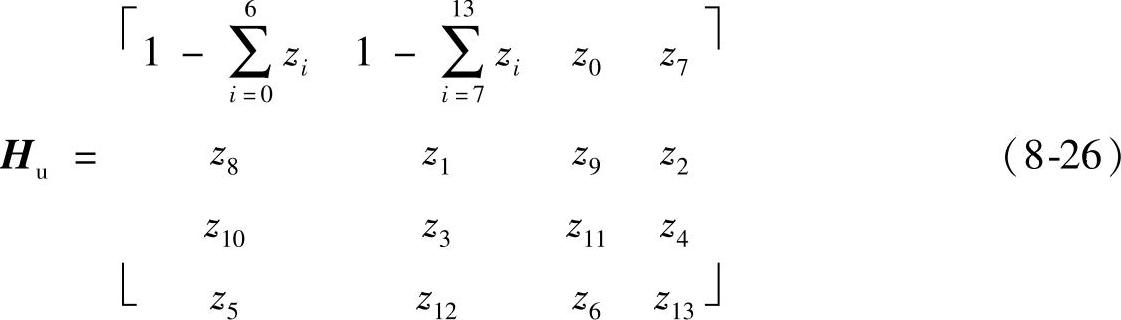
定制滤波器H1/8（其反变换即为非重叠模板T1/8）如下：
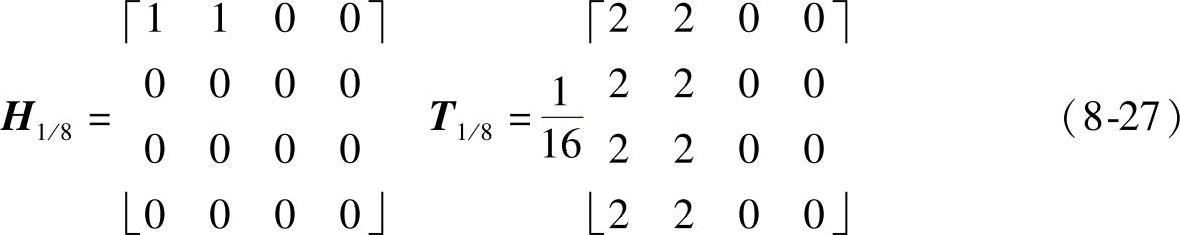
有关全相位数字信号处理方法及MATLAB实现的文章
- 详细阅读
-
基于二维傅里叶变换的内插模板优化技术详细阅读
正交基为傅里叶算子时，模板设计过程与上面沃尔什算子基本相同，不同之处在于卷积类型变为循环卷积。傅里叶基设计的特点是可以构造任何大小的内插模板，而不限于2的整数次幂。......
2023-06-23
-
基于二维DCT变换的内插模板技术详细阅读
由第5章内容可知，二维DCT运算可以转化成DFT运算，然后取结果的实部作为DCT变换的结果。DCT基可以设计任何大小的内插模板，而不限于2的整数次幂。以上面傅里叶基构造的结果直接得到DCT基滤波器H和对应的非重叠模板。图8-1c对应的定制H1/3如下，其反变换即为非重叠模板T1/3。......
2023-06-23
-
二维沃尔什和哈达玛变换详解详细阅读
沃尔什基矩阵与一维变换时相同，由沃尔什函数产生。由沃尔什矩阵可以构成二维沃尔什函数的基本图像。表5-24 阶沃尔什基本图像矩阵与傅里叶基本图像不同的是，沃尔什变换等其他正交变换基图像均是实矩阵。二维哈达玛变换基矩阵与沃尔什基矩阵只是行向量排列顺序不同，正反变换形式相同。......
2023-06-23
-
了解沃尔什正交基详细阅读
图4-14 阶沃尔什基函数对于N阶沃尔什变换基，定义在N点间隔内过零次数的一半定义为列率。由表4-1可看出，按列率排列的沃尔什基序号k是过零次数，故对应列率k/2；反之，沃尔什基的沃尔什变换是仅在列率为k/2时非零的N向量。性质1：两个不同列率的沃尔什基形成完备正交系，即基相乘产生列率搬移。表4-2 N=8列率搬移性质2：信号并元移位s的沃尔什变换等于信号沃尔什变换与列率s和沃尔什基乘积。......
2023-06-23
-
理论与实践：1/K内插模板设计在正交变换下的详细阅读
假设输入图像大小为N×N，则在某正交变换对α和β下1/K内插模板设计过程如下：1）写出1/K单位抽取算子d，d中只有N2/K个元素为1而其余为0。离散沃尔什变换简单、直观，其正交基只有两种状态，用它来表示图像的物理性质较为清楚，因此用沃尔什变换设计的各种图像处理模板系数都是有理数，且规则性强、易于归纳总结。用离散傅里叶变换设计的模板系数是无理数，但它却有明确的物理意义。......
2023-06-23
-
基于Boost变换器的MPPT仿真优化详细阅读
V1为电压传感器，用于检测光伏电池板输出电压。图7-9 定/变步长电导增量法MPPT功率跟踪效果对比图通过对不同MPPT算法的仿真，可以看到几种算法在进行最大功率追踪时的效果差异。这里的MPPT_mohu系统函数主要用于计算E=dP/dU和图7-10 基于模糊算法的MPPTSimulink仿真模型dE。......
2023-06-23
-
小皮卡尔和沃尔什的马里亚纳海沟深潜挑战：人类详细阅读
小皮卡尔和沃尔什没有任何畏惧，他俩下了最大的决心，鼓着最大的勇气，抱着必胜的信念，一定要深潜到马里亚纳海沟的深渊去探个究竟！上午7时许开始缓缓下潜。经过6个多小时的下潜，这艘重150吨的“的里雅斯特”号深潜器终于第一次把人类带到了世界大洋的最深点——马里亚纳海沟挑战者深渊。深潜器离大洋洋底只有5米，深度指示为11530米，该深度指示经订正后为10916米。......
2023-07-23
相关推荐