活动理论强调以学习者为中心，将学习者的学习看作是学习主体指向客体的活动，学习活动是影响网络课程质量及学习者在线学习效果的关键。不论学习者的地理位置或教育背景，MOOC都能为其提供高品质、大批量的在线学习课程，为学习者开展具体的学习活动提供支持。这就需要对MOOC中的学习活动进行精心的设计和有效的组织，以更好地促进学习者的在线学习。......
2023-11-07
理论与实践：1/K内插模板设计在正交变换下的应用
【摘要】：假设输入图像大小为N×N，则在某正交变换对α和β下1/K内插模板设计过程如下：1）写出1/K单位抽取算子d，d中只有N2/K个元素为1而其余为0。离散沃尔什变换简单、直观，其正交基只有两种状态，用它来表示图像的物理性质较为清楚，因此用沃尔什变换设计的各种图像处理模板系数都是有理数，且规则性强、易于归纳总结。用离散傅里叶变换设计的模板系数是无理数，但它却有明确的物理意义。
在第7章中分析并实现了二维信号的抽取和内插，信号处理过程可用图8-2表示。
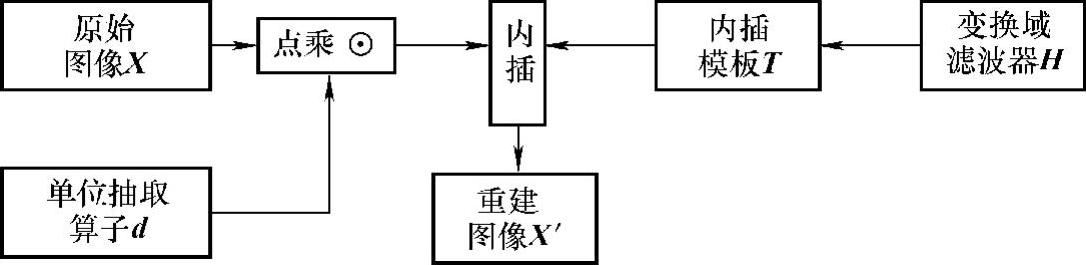
图8-2 图像的亚奈取样和基于模板的重建
图8-2表示原始图像X经过单位抽取算子d点乘后得到抽取图像A，通过选定某变换域并定义滤波器H来建立内插模板T，由T和D做卷积就可重建信号X。假设输入图像大小为N×N，则在某正交变换对α和β下1/K内插模板设计过程如下：
1）写出1/K单位抽取算子d，d中只有N2/K个元素为1而其余为0。求出d的调制点矩阵D，该矩阵只有K个元素为1而其余为0。D与d互为变换对，即
2）写出1/K抽取图像A。A中只有N2/K个图像元素保留而其余均为0。
A=X☉d （8-3）
A的变换域谱PA中由K个X谱组成，这K个A谱应没有重叠部分，否则会产生混叠误差。由正交变换域规律，在时域中相乘对应变换域卷积有
PA=X
D （8-4）
3）设计出从PA谱中滤出X谱的滤波器H，应符合以下条件：
PX=H☉PA （8-5）
4）H的逆变换即是非重叠内插模板T。内插重构图像X′可由T和A卷积得到，即
X′=T
A （8-6）
上面步骤中最关键的是设计滤波器H，显然H是低通滤波器，且为了保证A中的保留数据经过式（8-6）处理后不发生改变，模板T应满足一定的条件。假设X是全1的矩阵，结合式（8-3）和式（8-6）得到：
X=T
d=>PX=H☉D （8-7）
直流矩阵X的变换域谱PX在（0，0）处有唯一非零值1。此外，模板T与抽取算子d的取样处的点乘应等于1而其余位置为0（O是全1矩阵，Z是O的反变换），即
Z=T☉d=>O=H
D （8-8）
基于不同的正交变换对应不同的滤波器，变换域中的数值含义也不相同，但它们都从不同的基函数说明了信号的频率分布。在众多正交变换中，最主要的是傅里叶、沃尔什和DCT变换。离散沃尔什变换简单、直观，其正交基只有两种状态，用它来表示图像的物理性质较为清楚，因此用沃尔什变换设计的各种图像处理模板系数都是有理数，且规则性强、易于归纳总结。DCT变换避免了复数运算且能直观反映出能量分布规律，在MPEG-X等压缩算法中常用。用离散傅里叶变换设计的模板系数是无理数，但它却有明确的物理意义。下面分别选定二维Walsh、傅里叶和DCT正交变换域，构造1/2、1/3、1/4和1/8内插模板。
有关全相位数字信号处理方法及MATLAB实现的文章
- 详细阅读
-
辗转相截法：1，K，1，K循环截果详细阅读
E=C0+C1，C0=KC1+C2，C1=C2+C3，C2=KC3+C4，……只要我们给出（m0，m1，m2，……这节，我们也试图找出（1，K）循环截的逼近的亏、盈有理序列的递推生成规律。从一个循环节得p1，q1，r1，S1，从两个循环节得p2，q2，r2，S2。），可称这为（K，1）循环截。可知，从C0=C1+C2起的无穷截为（1，K）循环截，故这便为（K，1）循环截的的根式表达。）决定的m0增大，趋向0+（1，m1……推（1，K）循环截递推公式时，为啥我们只应公度C1，C3，C5，……......
2023-10-21
-
沃尔什内插模板简介详细阅读
显然，采用这种重叠滤波器内插就可以消除高列率谱的混叠。模板与图像做尺寸为3×3的卷积即得重叠滤波的全部输出，其结果与全部2×2子图像逐行逐点移动作低通滤波器后的叠加输出平均相同。显然，这就是我们在第5章中设计的二维全相位滤波器或称全相位内插模板。全相位沃尔什内插模板的设计就是给定低通滤波器H求出模板T的过程。......
2023-06-23
-
维生素K1、K2、K3的检测方法优化详细阅读
维生素K1、K2、K3由于分子式不同，所以很容易被分开。但是维生素K1和K2有反式和顺式之分，而顺式维生素K1、K2被认为是没有活性的，所以在测试过程中必须把顺式维生素K1和K2从反式维生素K1、K2中分离出去。测试步骤测试维生素K的样品准备可按第1章“1.3样品及标准溶液的配制”操作。为了有效地从样品中萃取油溶性维生素，建议整个萃取过程在70℃的水浴条件下进行。水的比例不要超过10%。......
2023-07-02
-
东亚法治：全球化下的理论与实践详细阅读
这种对西方法治的引进和吸收，构成了东亚共通法治的近代基础。近年来，东亚地区内的相互贸易额逐年增长，区域内贸易比例早已突破50％，这个比例高于北美自由贸易区而略低于欧盟。......
2023-11-28
- 详细阅读
-
全球化下东亚法治的理论与实践详细阅读
实际上，有种种方式可以解决或避免发生国际法与国内法之间的冲突。对此，我国学者李龙等认为，法律规范的和谐一致是准确把握国际法与国内法关系的理论始点，法的内在特质的普遍性与形式特征的共同性以及法治社会对法律体系融......
2023-11-28
-
VR理论与应用开发实践详细阅读
像之前主角的动画一样，给怪物添加Animator Controller。图8-192怪物移动时播放动画怪物攻击新建两个脚本EnemyAttack处理怪物攻击，PlayerHealth处理角色的生命值。图8-193PlayerHealth脚本EnemyAttack如图8-194所示。图8-195怪物预制体加入碰撞体确定isTrigger的选项勾上，并将脚本挂在怪物身上。图8-196选择isTrigger图8-197单击Apply图8-198触发碰撞体......
2023-10-17
相关推荐