设计模板的全相位方法详解

2023-06-23 理论教育版权反馈

【摘要】：在一维信号处理中，用来抑制噪声干扰并保留原有有用信号的滤波方法以及获得各种信号变换的数字滤波器，有着极其重要和广泛的应用。所以，统计结果表明二维图像信号谱能量90%以上集中在二维低频区域，如果进行2∶1或更高亚取样，谱也未发生重叠。为了克服边缘效应，一种有效的方法是对图像进行重叠滤波，在重叠滤波中的子图像在行列方向上逐点进行重叠。

在一维信号处理中，用来抑制噪声干扰并保留原有有用信号的滤波方法以及获得各种信号变换的数字滤波器，有着极其重要和广泛的应用。同样，对于二维和多维信号的处理，各种二维数字滤波方法和信号变换的二维数字滤波器在实际中也有着许多重要的作用。如果将具有理想频率响应H_d（u，v）的二维滤波器的冲击响应函数h_d（α，β）在抽样间隔分别为Δα和Δβ的离散点上进行抽样，则可用所得的理想样本值h_d（m，n）的函数：

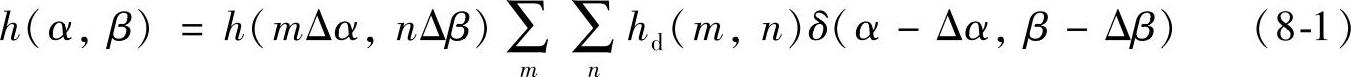
来近似地代表原来的h_d（α，β）。其中的α和β应为离散变量，离散冲激响应与输入离散信号进行滤波的数字运算，相应的滤波器是二维数字滤波器，在二维数字信号处理如图像中应用十分广泛。

按照奈奎斯特取样定律取样并编码得到的数字信号具有较大的数据量，在数字存储及通信中常常考虑如何压缩图像以提高存储效率及节省带宽。最直接的方式是在原图像矩阵的基础上进行再抽取，这种抽取可以在行和/或列向上隔M点抽取来实现，这种在经过奈奎斯特取样得到的数字信号基础上再取样的过程称为亚奈奎斯特取样（简称亚奈取样）。图8-1显示了几种1/K二维亚奈取样结构。

图8-1 二维亚奈取样结构示例

在节省数据量的同时需要考虑的问题是如何重建亚奈信号，主要基于以下几点：一是利用各种摄像设备获取的自然界图像有水平和垂直两个清晰度，但由于地球重力的影响，实际图像或是要求高的水平清晰度（即垂直细条组成的高频线），或是要求高的垂直清晰度（即水平细条组成的高频线），很少有图像要求水平和垂直清晰度都是高的（相当于噪声）。所以，统计结果表明二维图像信号谱能量90%以上集中在二维低频区域，如果进行2∶1或更高亚取样，谱也未发生重叠。二是图像主观质量不完全取决于信噪比，与人眼观察具有低通特性、对色度敏感度低于亮度等因素都有关系，故在确保信噪比高于主观察觉门限值之上就可进行高亚奈取样。

图像的内插处理中，常将图像分解成许多子图像，这种有限的正交变换处理方法由于只能反映图像在局部的频谱分布，因此在块与块的交界处或图像边缘处会引起图像质量的损伤。为了克服边缘效应，一种有效的方法是对图像进行重叠滤波，在重叠滤波中的子图像在行列方向上逐点进行重叠。如果子图像的尺寸为N×N，则对任一取样点，与该点有关的互相重叠的子图像为N²个，这N²个子图像的输出之和的平均即为重叠滤波的输出。重叠滤波最终可表示为一个（2N-1）×（2N-1）的模板，模板和原始图像做一般卷积即可得处理后的结果。它基本消除了边缘效应，图像的其他性质也有明显的改善。

设计模板的全相位方法详解

相关推荐