一维信号分解与重构方法优化

2023-06-23 理论教育版权反馈

【摘要】：对高斯白噪声分别采用图7-23中3种条件下ap1 nsd滤波器进行分解和重构，取样点数为100，分解得到的低频、高频及重构信号和误差结果如图7-27所示。若信号频谱分布在π/2处分量较少，则可采用H0和H1进行分解和重构。图7-29 条件1下ap1 d半带高低通滤波器由图中可见，重构误差小于2%，通过增加滤波器阶数可进一步降低重构误差。由图7-29可知剩下的信号分量可无失真重构，而对于π/2分量则按照带宽的占比进行高比下取样。

对高斯白噪声分别采用图7-23中3种条件下ap^{1 nsd}滤波器进行分解和重构，取样点数为100，分解得到的低频、高频及重构信号和误差结果如图7-27所示。

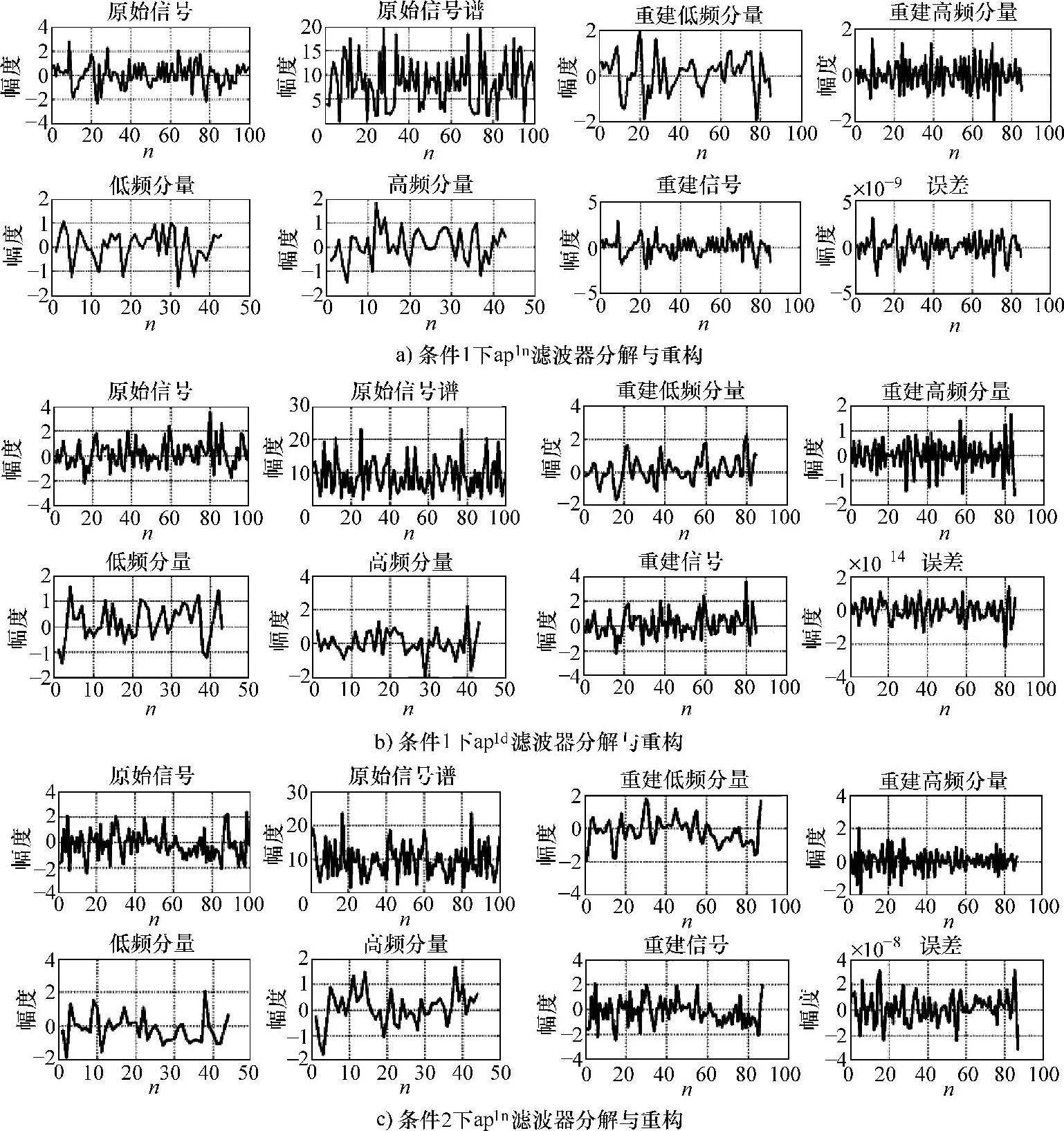
图7-27 ap^1nd设计的2QMFB分析和重构试验

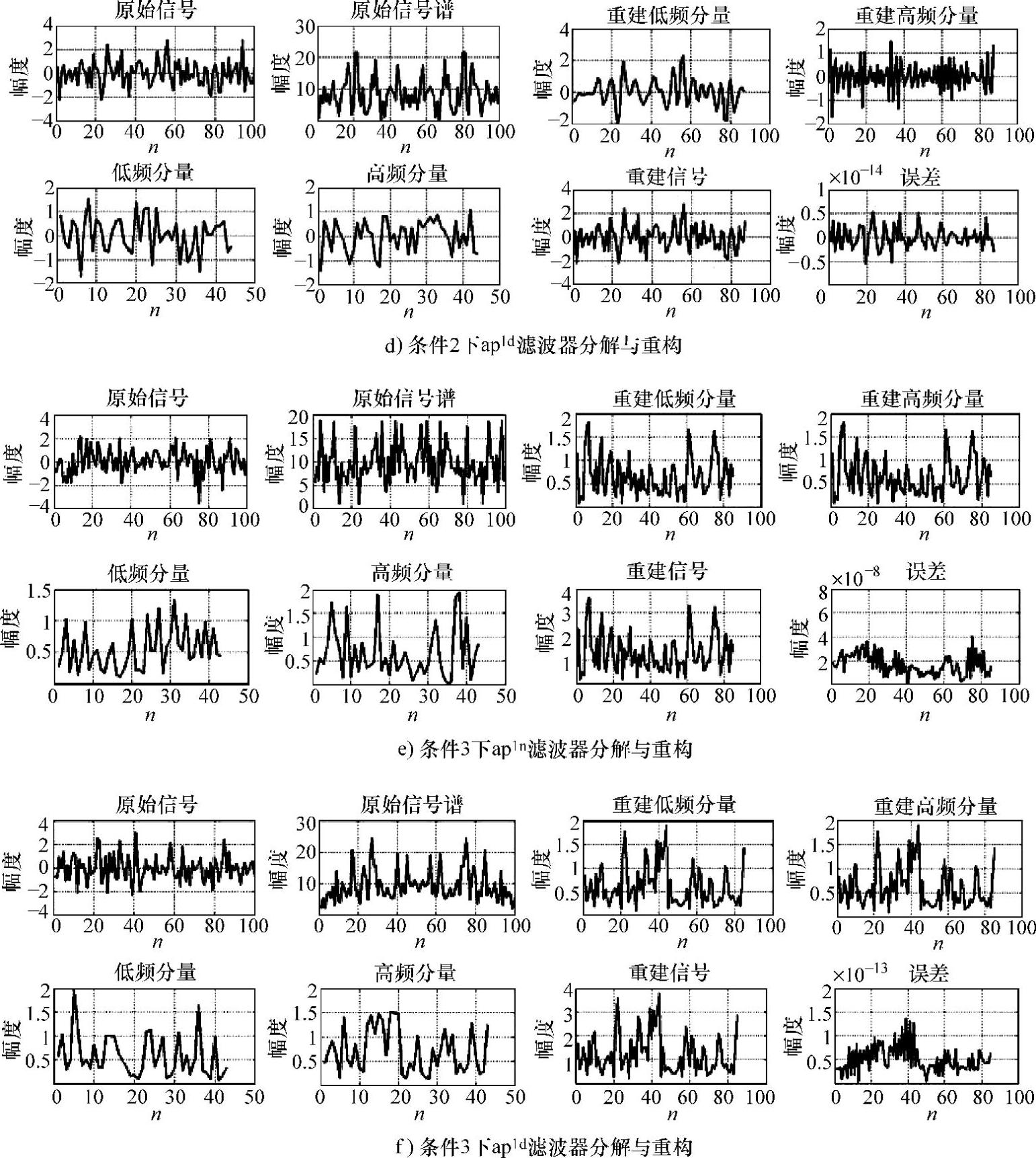
图7-27 ap^1nd设计的2QMFB分析和重构试验（续）

上面的实验结果验证了ap^1nd设计2QMFB的正确性。需要说明的是，第三类条件设计的滤波器组不具有线性相位，因此只对幅度误差进行了分析。结果显示，ap¹ⁿ重构的误差为10^-8，而ap^1d则达到了10^-14左右，基本达到完全重构的目标。3种条件下的ap^{1 s}，重构误差则较大，ap^{1 s}条件1下的实验结果如图7-28所示。

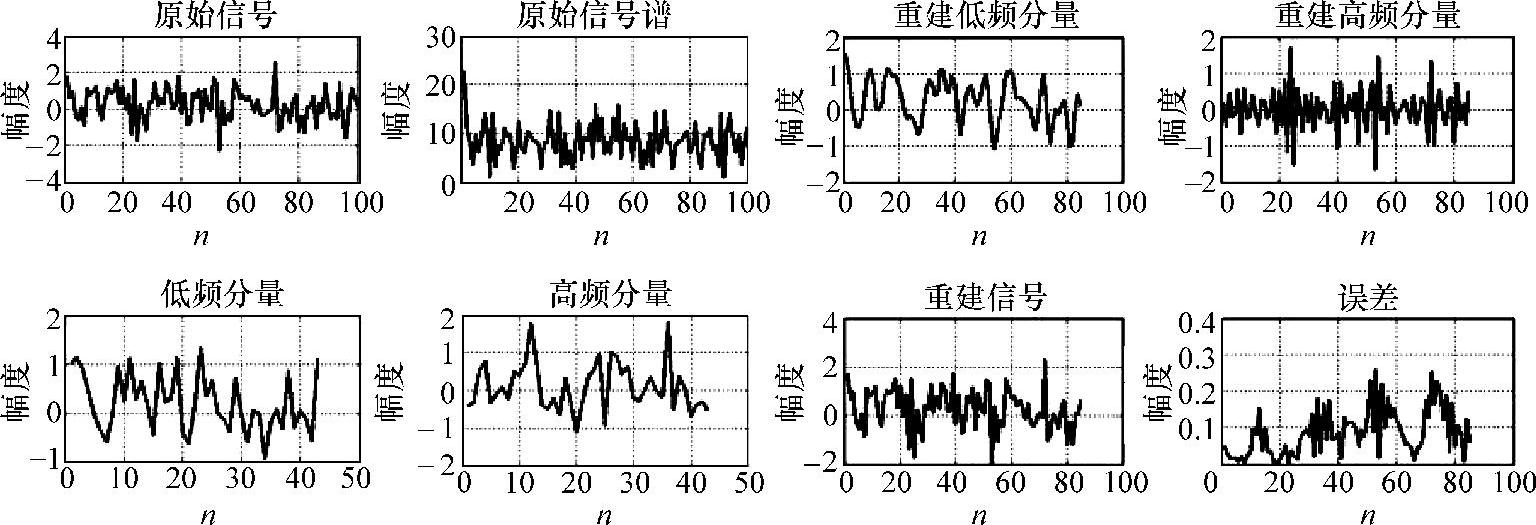
图7-28 ap^{1 s}设计的2QMFB分析和重构试验

实现以上实验结果的MATLAB代码如下（省去绘图部分）：

ap¹设计得到的2QMFB最大的优点是重建误差精度高，但也存在3个问题：一是恢复得到的信号有N-1个延迟，从上面的程序可以看出；其二是运算过程涉及零点统计与谱分解，比较复杂；其三是形成的高低通滤波器H₀和H₁并不满足子带互补，这由图7-23实验结果得到证实。实际上，子带互补和功率互补不可能同时实现，矛盾之处在于过渡带。实际上，按照ap^{1 nsd}很容易形成严格互补的半带滤波器组H₀，H₁。若信号频谱分布在π/2处分量较少，则可采用H₀和H₁进行分解和重构。如采用N=64设计得到的ap^{1 d}高低通半带滤波器及特性如图7-29所示。

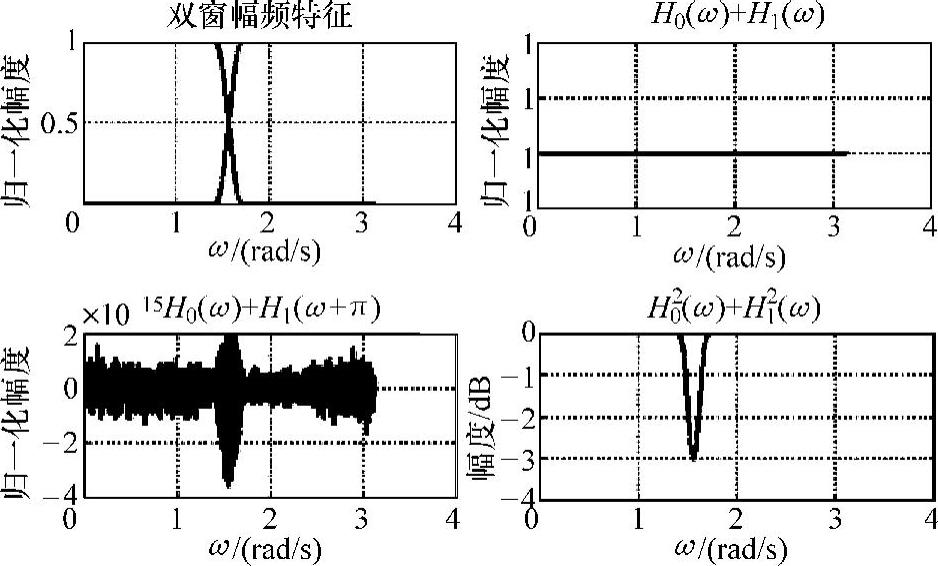
图7-29 条件1下ap^{1 d}半带高低通滤波器

由图7-29可以看到，ap^{1 d}高低通半带滤波器是严格子带互补的，且成镜像对称关系，而功率谱则在过渡带出现3dB误差。利用此滤波器组针对长度为200、占空比为50%的方波进行分析和重构的结果如图7-30所示。

由图中可见，重构误差小于2%，通过增加滤波器阶数可进一步降低重构误差。此外，还可以根据信号谱分布的规律，预先过滤出π/2分量。由图7-29可知剩下的信号分量可无失真重构，而对于π/2分量则按照带宽的占比进行高比下取样。对比谱分解，此方法的优点有二：一是构造简单，按照条件1/2/3的抽样序列H进行设计即可得到分析和综合滤波器，无需谱分解；二是高低通滤波器严格子带互补，因此两通道完全包含了信号全部谱信息，这点很重要。尤其对于不是以重构为目标的应用如信号分析，子带提取等方面相对ap QMFB和小波来说具有一定优势。实现图7-29和图7-30实验结果的MATLAB代码（绘图部分省略）如下：

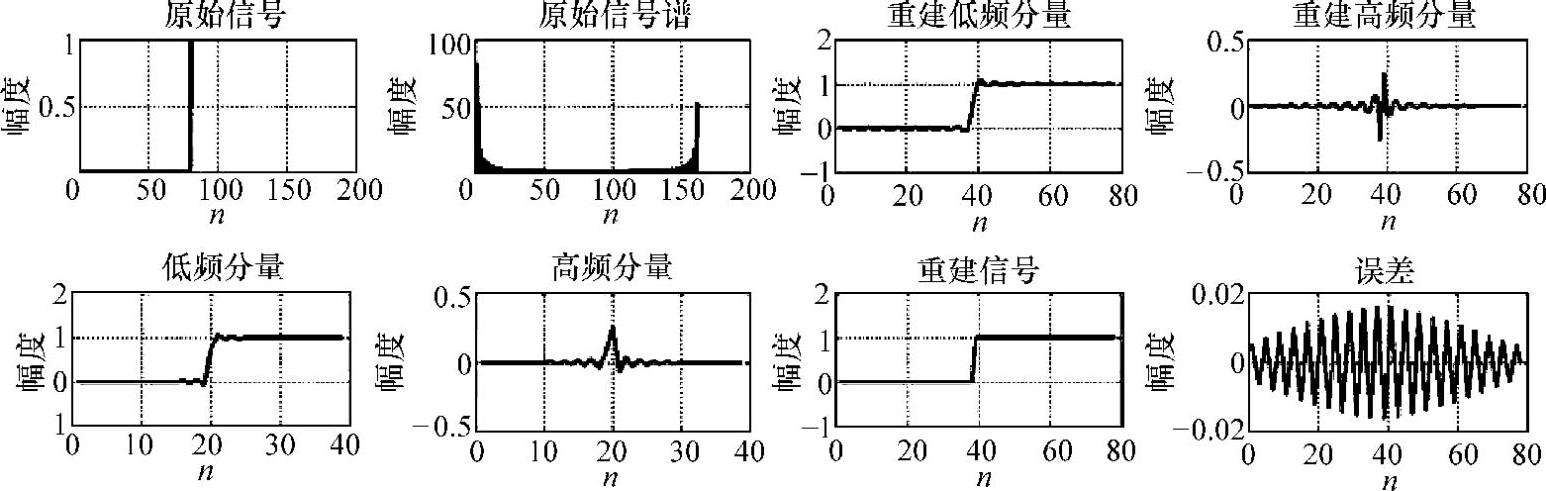
图7-30 ap^{1 d}半带高低通滤波器分析与重构

一维信号分解与重构方法优化

相关推荐