基于边缘的分割方法边缘检测是在灰度图像分割中广泛应用的一种技术,它基于在区域边缘处梯度变化剧烈的假设,试图通过检测区域间的边缘来达到图像分割的目的。则分割时,选取的阈值应位于直方图波谷处。......
2023-06-28
基于分解子带的图像编码称为频带分割编码,其基本思想是把信号分解成低分辨率的平滑近似和高频细节两部分,分别称为低频子带和高频子带。对每个生成的子带又可以用同样的方式进一步分解。对于图像的分解通过在水平和垂直方向上分解来实现。然后,对于不同分辨率的子带图像采用不同的量化精度和编码方法来达到图像压缩的目的。Mallat在多分辨率分析理论的基础上,用子带结构实现离散小波变换的算法,统一了子带滤波与小波变换的计算,使小波变换成为图像处理的重要手段,为图像压缩和编码提供了有效的方法。
一幅图像可看成二维信号,经小波变换后产生了4个子带图像,即水平和垂直方向低频子带LL,垂直方向低频和水平方向高频子带HL,水平方向低频和垂直方向高频LH以及水平和垂直方向都是高频子带HH。分解方式如图7-24所示。图7-24中子带Cj-1集中了图像的大部分能量,大部分幅值较大的系数集中在该子带中,以后的小波变换都是对前次变换产生的低频子带进行变换。图7-25说明了一幅图像经过二级小波变换的过程以及形成的各个子带分布。从图中可以看出,二维数字信号的离散小波变换最终转化为数字滤波。对于紧支小波,相应的滤波器类型是FIR,滤波器系数由尺度函数与小波函数决定。某些情况下,滤波器的线性相位特性可避免不必要的失真。为了得到线性相位滤波器须要求FIR系数对称,为此需设计对称的小波函数。另一方面,小波基的正交性限制了所能得到的小波基类型,特别是除了Harr小波外,没有任何紧支正交小波具有对称性。为此,考虑设计基于ap2的图像分解和重构。
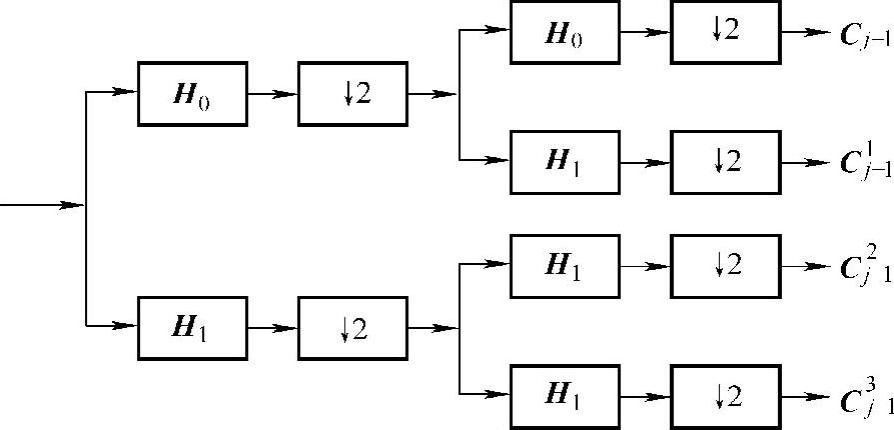
图7-24 二维信号分解
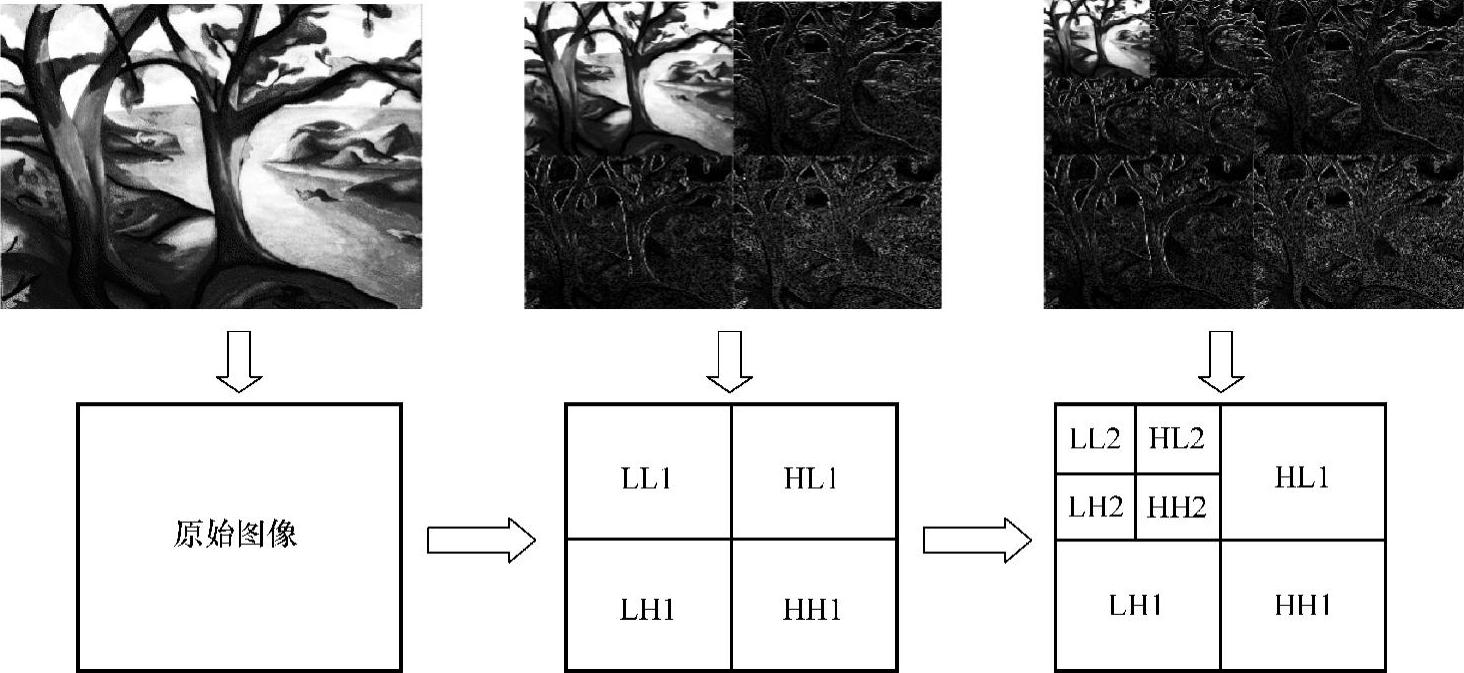
图7-25 图像的子带分解(db小波)
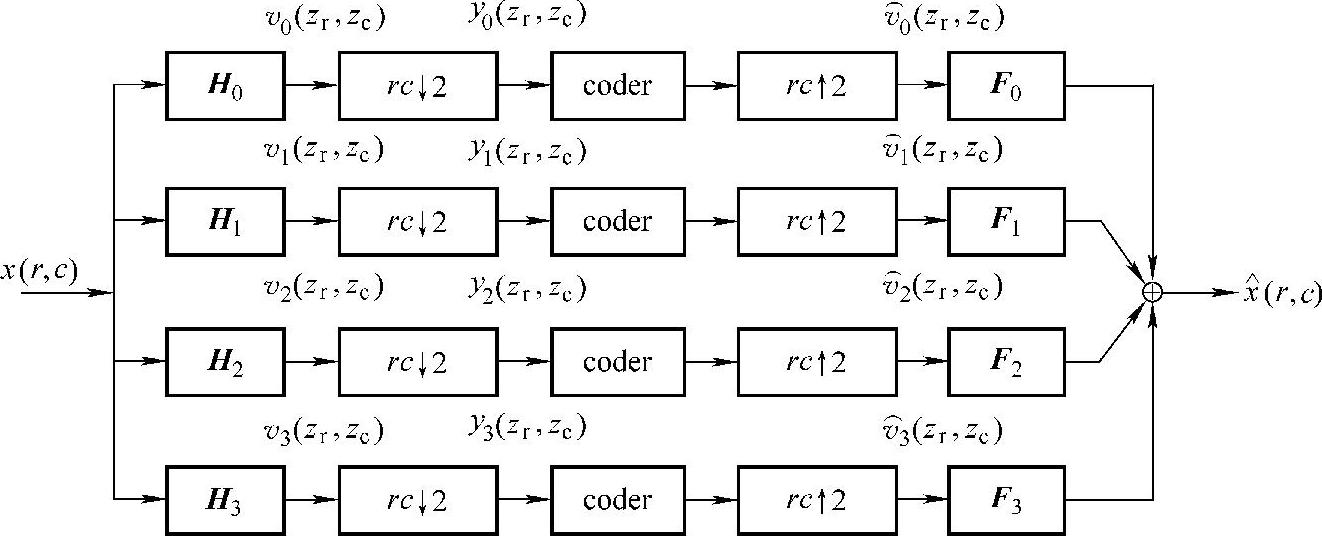
图像的子带分解及重构对应二维四子带QMFB,结合图7-9和图7-18,系统原理图如图7-26所示。
由图7-26可知:
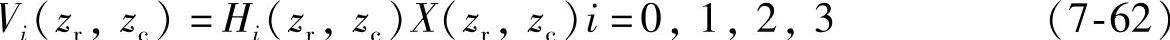
经二维2∶1下取样得:
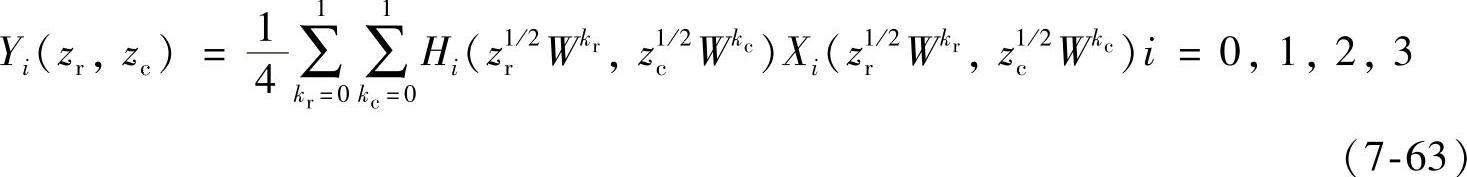
图7-26 二维四子带QMFB
经综合滤波器得:
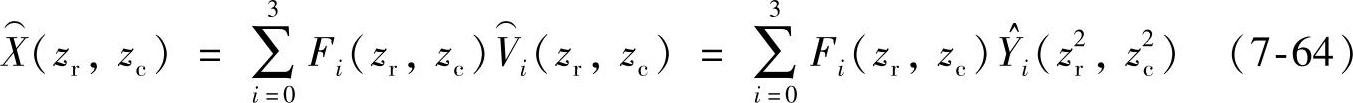
若忽略编码误差,将式(7-63)代入到式(7-64)中并整理得:
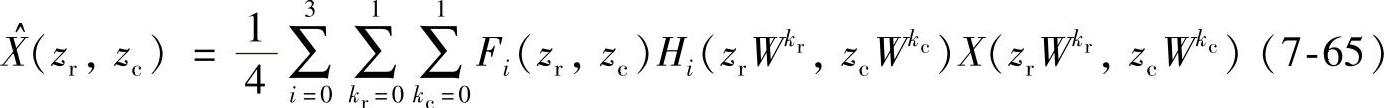
定义如下矩阵和向量:
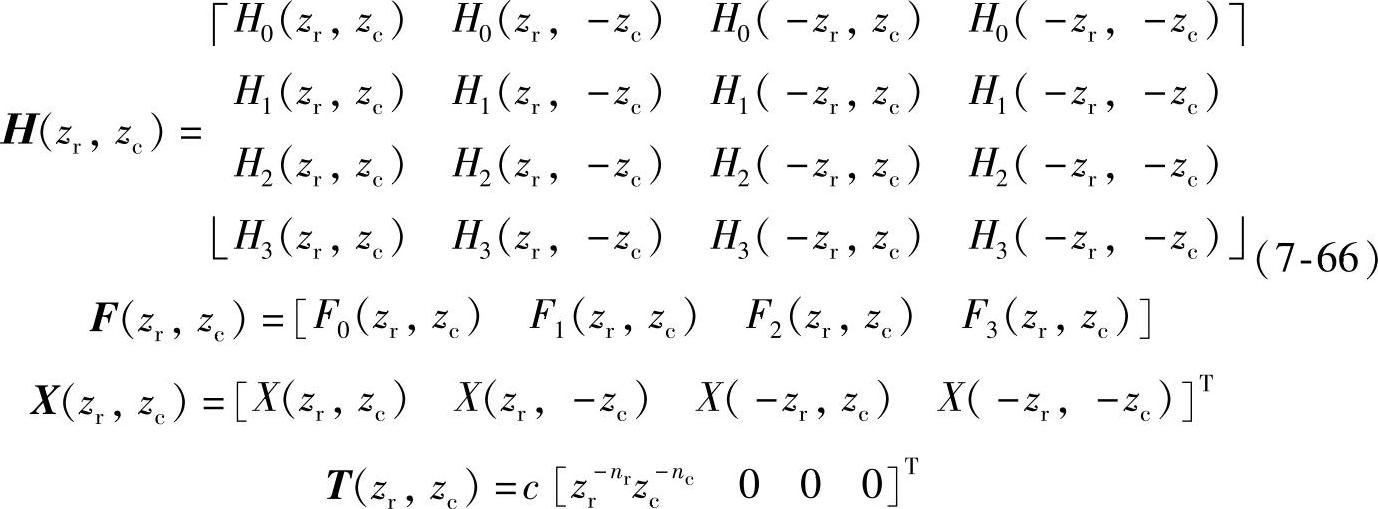
其中H称为重叠矩阵,式(7-65)可重写成如下:

若完全消除混叠失真,要求:
F(zr,zc)H(zr,zc)=T(zr,zc) (7-68)
这样,就可以由分析滤波器求出综合滤波器F,但结果难以保证是FIR滤波器组,利用多相分解可以解决,但过程复杂。实际上,对于二维图像的分解可通过一维滤波器分别在行列方向上进行。
有关全相位数字信号处理方法及MATLAB实现的文章

基于边缘的分割方法边缘检测是在灰度图像分割中广泛应用的一种技术,它基于在区域边缘处梯度变化剧烈的假设,试图通过检测区域间的边缘来达到图像分割的目的。则分割时,选取的阈值应位于直方图波谷处。......
2023-06-28

但是大多数区域分割都是非规则的形状,这时可以采用基于区域特性的图像分割方法,例如区域生长法、区域合并分裂法等。区域生长法也称为区域扩张法,其基本步骤可以如下描述。3)将获得的新区域当做新的种子区域继续进行2)的过程,直到没有满足条件的像素点时停止生长。4)区域生长停止的条件 即合适种子点停止生长。一般情况下,区域生长停止条件是结合生长准则来进行合理的设定。......
2023-11-24

早期的图像分割研究主要集中于对狭义图像分割的研究,且并未区分狭义图像分割与目标分割的概念,界定比较模糊。3)图像仅是现实世界的表象。只有随着各学科的综合发展,目标分割才会不断有新的突破。总之,尽管长期以来人们为研究目标分割问题做出了很大努力,但上述原因导致很难实现一种普适的方法,而只能针对特定问题和具体的需求给出合理的解决方法,在处理速度、精度等关键性指标上做出均衡或侧重。......
2023-06-28

如果,预先知道每个目标占整个图像的比例p,则可以采用p参数法进行分割。下面以图像中包括两个区域的情况来分析p参数法的基本步骤。由于这种方法需要预先知道各个区域的p值,因此被称为p参数法。 p参数法图像分割实例本例仍以图4.39a为例进行p参数法图像分割,假设p=0.4。图4.39 p参数法图像分割实例从图4.39c中可以看出,当Pa1=0.4,其对应的灰度值为200,因此分割阈值T=200。......
2023-11-24

对整体特征进行有效的理解和研究,必须要明确目标分割的定义以及它与图像分割之间的关系。通常它包含较广的含义,进一步可以细分为面向图像特征的图像分割和面向物理、语义特征的目标分割。令I表示一幅n×m的待分割图像,则图像分割的定义可形式化的表示为将I划分为满足下述条件的N个子区域Ii,(i=1,2,…,N且i≠j,S 是对Ii中所有元素属性相似性描述的逻辑谓词。图2-3所示为图像分割与目标分割的例子。......
2023-06-28

为了节省存储空间和提高传输速度,图像压缩编码是非常重要的多媒体技术之一。表5.1图像数据量数据压缩可分成两种类型:无损压缩和有损压缩。无损压缩是指使用压缩后的数据进行重构,重构后的数据与原来的数据完全相同。无损压缩用于要求重构信号与原始信号完全一致的场合,例如行程长度编码、哈夫曼编码等。表5.2列出了常见的图像文件格式所采用的压缩编码方法。......
2023-10-22

5.7基于声呐图像划分海底底质类型通过海底声反射和声散射等手段可以进行海底底质的声学特征研究,海底底质声学特性一直是海洋地质、水下工程地质、海底矿产资源、海洋渔业和水下通讯等领域重要的研究内容。......
2023-11-29

长度为N的单边带H0按上面3种方法设计生成的ap半带滤波器H的长度为2N-1。在满足条件1、2、3下,ap1 nsd半带滤波器H、单边带H0和卷积窗C的零点分布如图7-22所示。ap1ns半带滤波器的H零点由单位圆上和内及对应的倒数组成,而ap1 d半带滤波器的H零点只由单位圆内及对应的倒数组成。即把半带滤波器H进行分解后找到所有圆内的零点就可以确定分析低通滤波器h0,再按照PR条件即式关系依次求出分析高通滤波器h1,综合滤波器f1和f2。......
2023-06-23
相关推荐