全相位半带滤波器设计方法

2025-09-29 理论教育版权反馈

【摘要】：目前，半带滤波器常用的设计方法有窗函数法、拉格朗日插值法和单带滤波器法，下面分别给以简单介绍。G和g求出后，再对g做2倍插值，并令插值后的序列中心等于0.5，即3.单带滤波器法首先用Chebyshew最佳一致逼近法设计出一个单带滤波器G。观察式，令：图7-19 全相位法与其他3种设计半带滤波器对比运行结果如图7-19所示。

由上面结论可知，如果h（n）是实序列，则半带滤波器G（e ^jω）满足：

G（e ^jω）=H（e ^jω）H（e ^jω）=|H（e ^jω）|²≥0 （7-35）

即实系数单位冲激响应设计的半带滤波器幅频特性横为非负。这样，只要设计出半带滤波器G（z），然后再谱分解即可得到功率对称滤波器H₀（z），继而得到H₁（z），而H₀（z）和H₁（z）满足功率互补特性，即按照（7-35）设计就可以得到PR的内插滤波器F₀（z）和F₁（z）。

目前，半带滤波器常用的设计方法有窗函数法、拉格朗日插值法和单带滤波器法，下面分别给以简单介绍。

1.窗函数法

假设要设计的半带滤波器截至频率ω_c=π/2，令理想滤波器的|H_d（e ^jω）|=1，对于|ω|≤π/2，其余为零，则

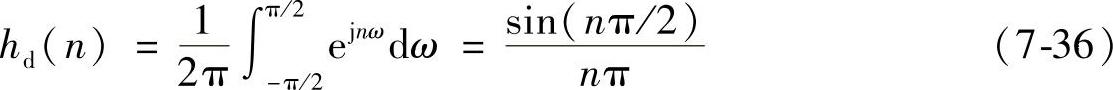
显然，单位冲激响应h_d（n）偶数项为0且中心点等于0.5，偶对称。所以，它是零相位的半带滤波器，选择长度为N=4J-1的窗函数w（n），并与移位2j-1后的h_d（n）相乘即得到最终半带滤波器的单位冲激响应h（n）为

h（n）=h_d[n-（2 j-1）]w（n）（7-37）

2.拉格朗日插值法

首先按照下式求出半带滤波器的单位冲激响应为

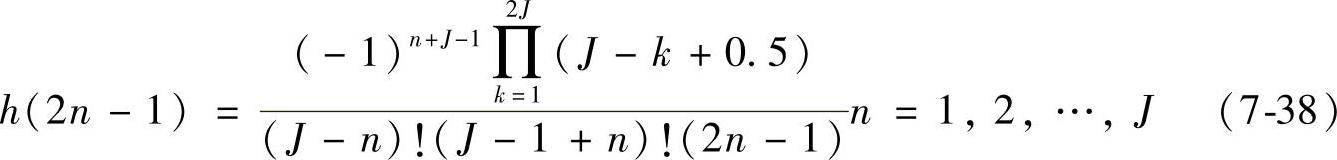
h（n）的总长度为N=4J-1。则对应的转移函数如下：

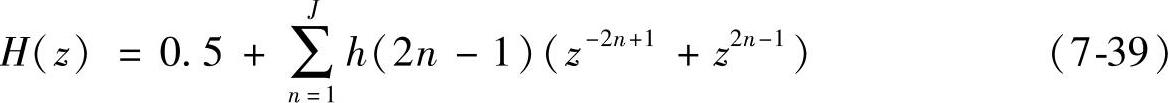
3.单带滤波器法

首先用Chebyshew最佳一致逼近法设计出一个单带滤波器G（z）。所谓“单带”是令G（z）的通带频率为2ω_p，阻带频率为π，即从2ω_p到π是过渡带，因此，G（z）没有阻带。令g（n）的长度为（N+1）/2，因为半带滤波器长度为N=4J-1，所以g（n）的长度为2J。G（z）和g（n）求出后，再对g（n）做2倍插值，并令插值后的序列中心等于0.5，即

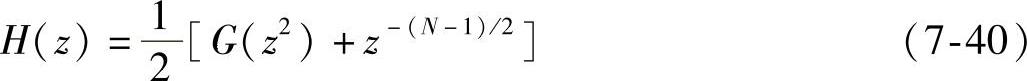
这样，H（z）是半带滤波器，其截至频率变为ω_p，通带和阻带内的波纹数分别是G（z）的一半。

由第2章中的结论可知，ap¹的频率取样序列H反映了系统传输特性，利用ap¹对H的线性性，可方便地实现严格子带互补的半带滤波器组。为满足在ω_m=π/2时的幅度等于0.5，只需设置H中下标为（ω_m/（2π/N））=N/4处的值为0.5，同时考虑到线性相位，对ap¹的频率取样序列H可作如下设定：

1）H中下标为0到N/4-1及3N/4到N-1的元素等于1。

2）H中下标N/4及3N/4-1的元素等于0.5。

3）H中其余元素等于0。

考虑如下低高通序列：

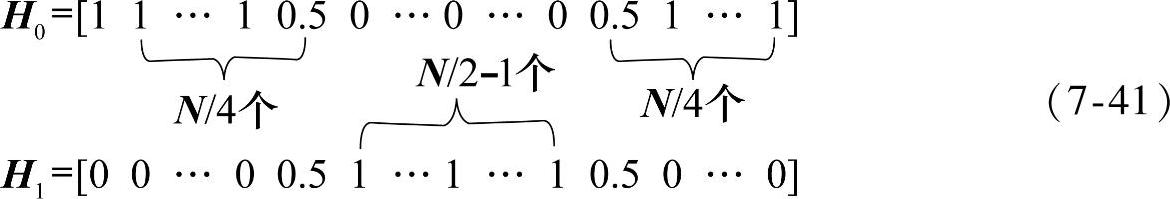
低通序列的单位脉冲响应序列等于：

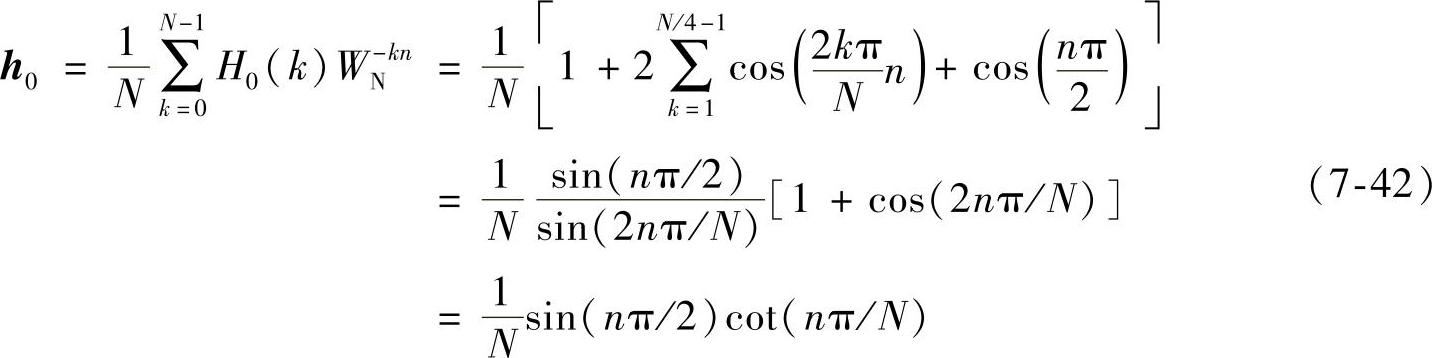
又H₀+H₁=1，所以由式（7-42）可得高通序列的单位脉冲响应序列如下：

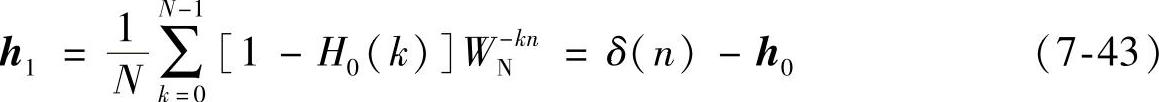
由式（7-42）和式（7-43）易知，h₁（0）=h₀（0）=0.5，其余偶数项均等于0而奇数项反相。结合式（2-51）有

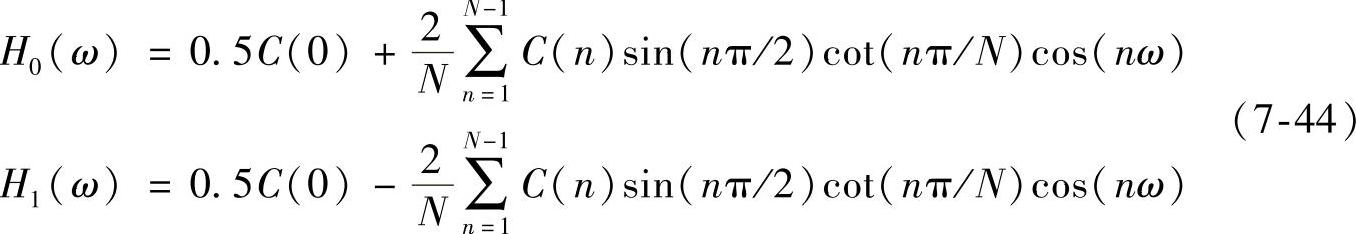
归一化卷积窗C（0）=1。由式（7-44）易知下式成立：

由上面过程可知，按照式（7-41）设置长度为N的H对应的ap¹是长度为2N-1的半带滤波器。半带滤波器h（n）满足：

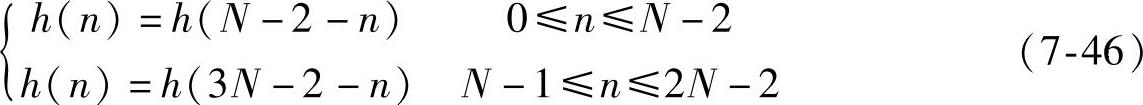
ap¹半带滤波器法与传统3种方法生成的滤波器的MATLAB代码如下：

(https://www.chuimin.cn)

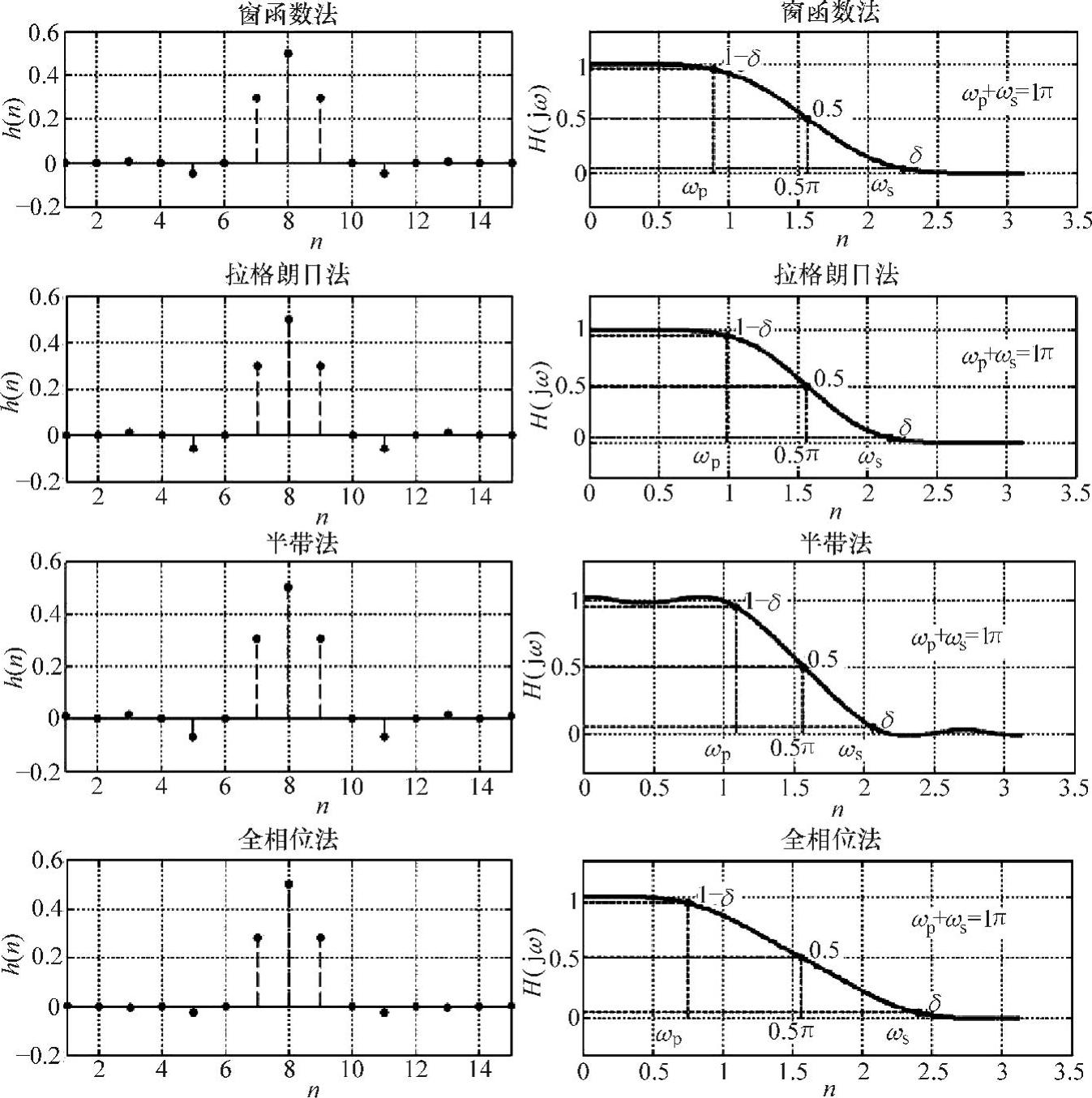
图7-19 全相位法与其他3种设计半带滤波器对比

运行结果如图7-19所示。由图7-19对比可看出，半带方法得到的滤波器具有最小过渡带宽度，但通带和阻带内的波纹也最多且出现负幅值，因此需要先进行抬升后才可以进行谱分解来得到分析滤波器H₀；ap法同窗函数法和拉格朗日法在通带和阻带保持很好的平滑性，但不同窗函数也会出现负幅值现象，拉格朗日法又相对复杂；ap^1nd法设计得到的半带滤波器幅值则横为非负，且设计方法简单，物理意义明确。

由第2章结论可知，具有线性相位的ap传输特性均可表示为余弦波的加权线性组合。观察式（7-44），令：

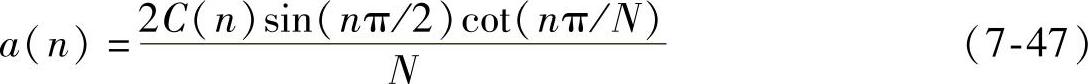
对于任意的角频率θ（-π/2≤θ≤π/2）结合a（n）偶数项为零，当n=2k-1（k∈Z）时，有

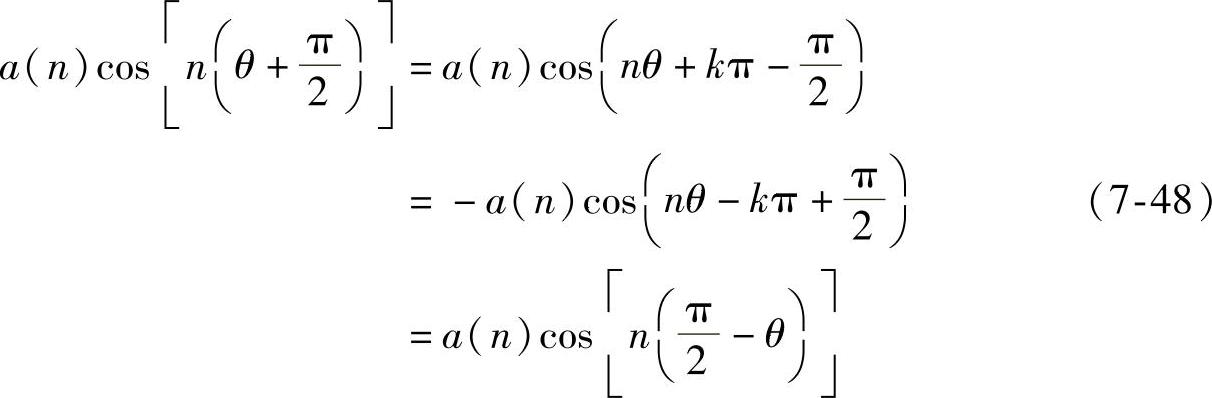
即ap曲线在角频率π/2处满足奇对称，如图7-20所示。

所以，如果冲激响应序列满足3个条件中的第2个即N=4L（L是整数），这样就可以通过设置H使在角频率π/2处等于0.5；若N不是4的整数倍即无法直接设置角频率π/2处的值，但通过式（7-48）可知，设置H在角频率π/2左右点分别为1和0（低通），则ap法得到的滤波器仍满足3个条件中的第二个，即

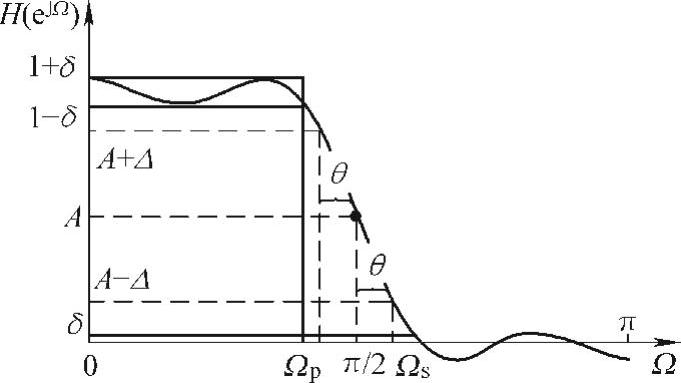
图7-20 全相位半带滤波器幅频关于π/2奇对称

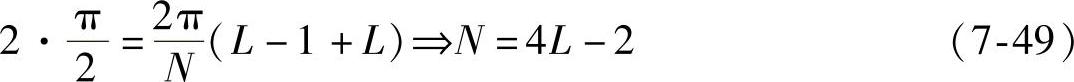
结合式（7-41），这时H₀结构如下：

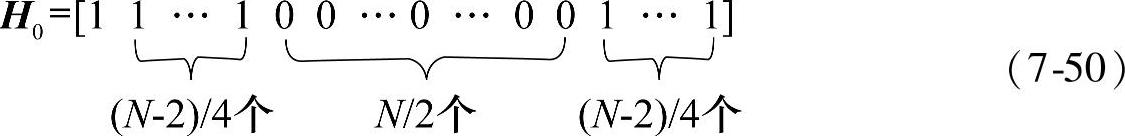
按照式（7-42）推导的过程，低通滤波器冲激响应为

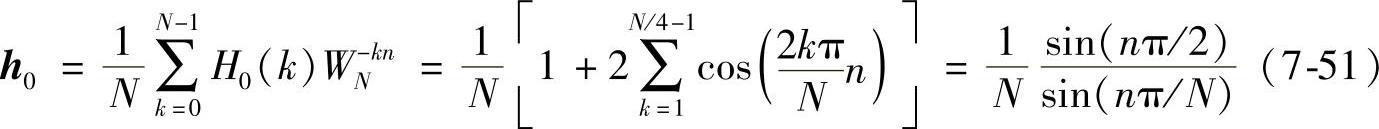
由式（7-51）易知，h₀（0）=0.5且偶数项为0并满足式（7-47）对称性。结合式（2-51）得到：

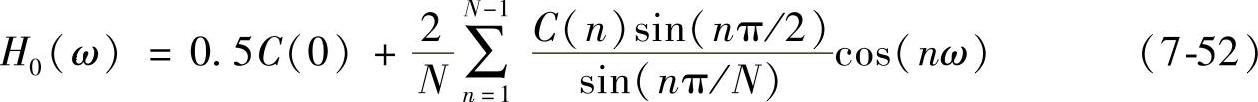
因为C（0）=1，所以H₀（π/2）=0.5，即H₀也是半带滤波器。

结合式（7-41）和式（7-42），假定低频取样序列H₀作如下定义：

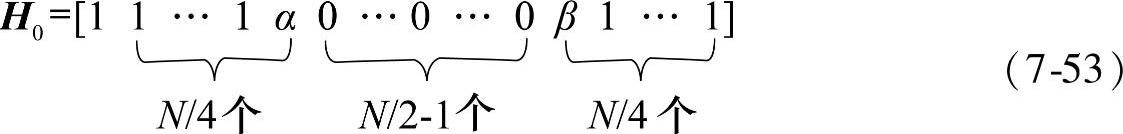
则容易求出：

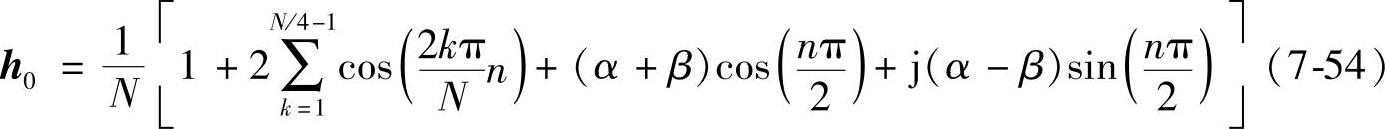
若α与β不等，H₀不再满足线性相位条件，因此h₀出现复数部分。但是，只要α+β=1，则容易得出下面结果：

所以，基于h₀构建的ap就是半带滤波器。取α=1（β=1时可类似处理），半带滤波器的传输函数如下：

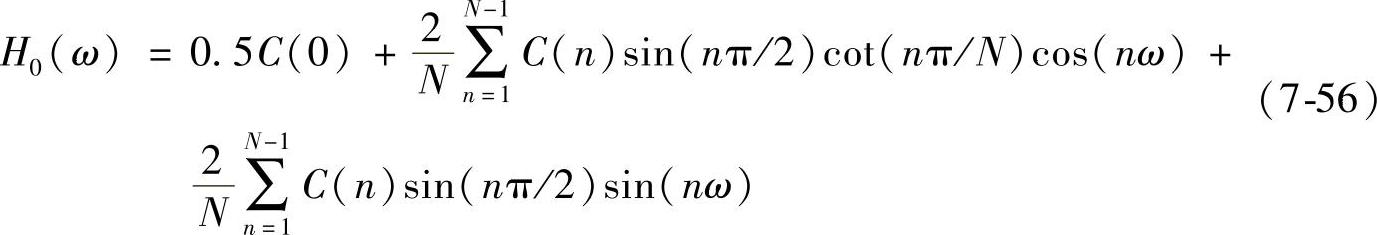
在频率点π/2处，幅值等于：

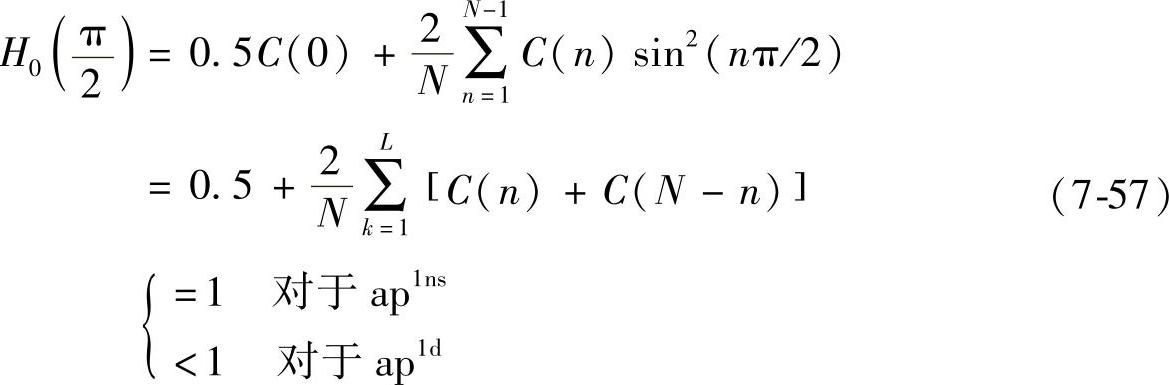
之所以不再等于0.5是因为h₀不是实数。式（7-41）、式（7-50）和式（7-53）表示的条件分别称为条件1、2和3。MATLAB实现条件2和3的ap^{1 nsd}半带滤波器代码（绘图部分省略，基本同函数semiB）如下：

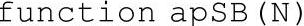
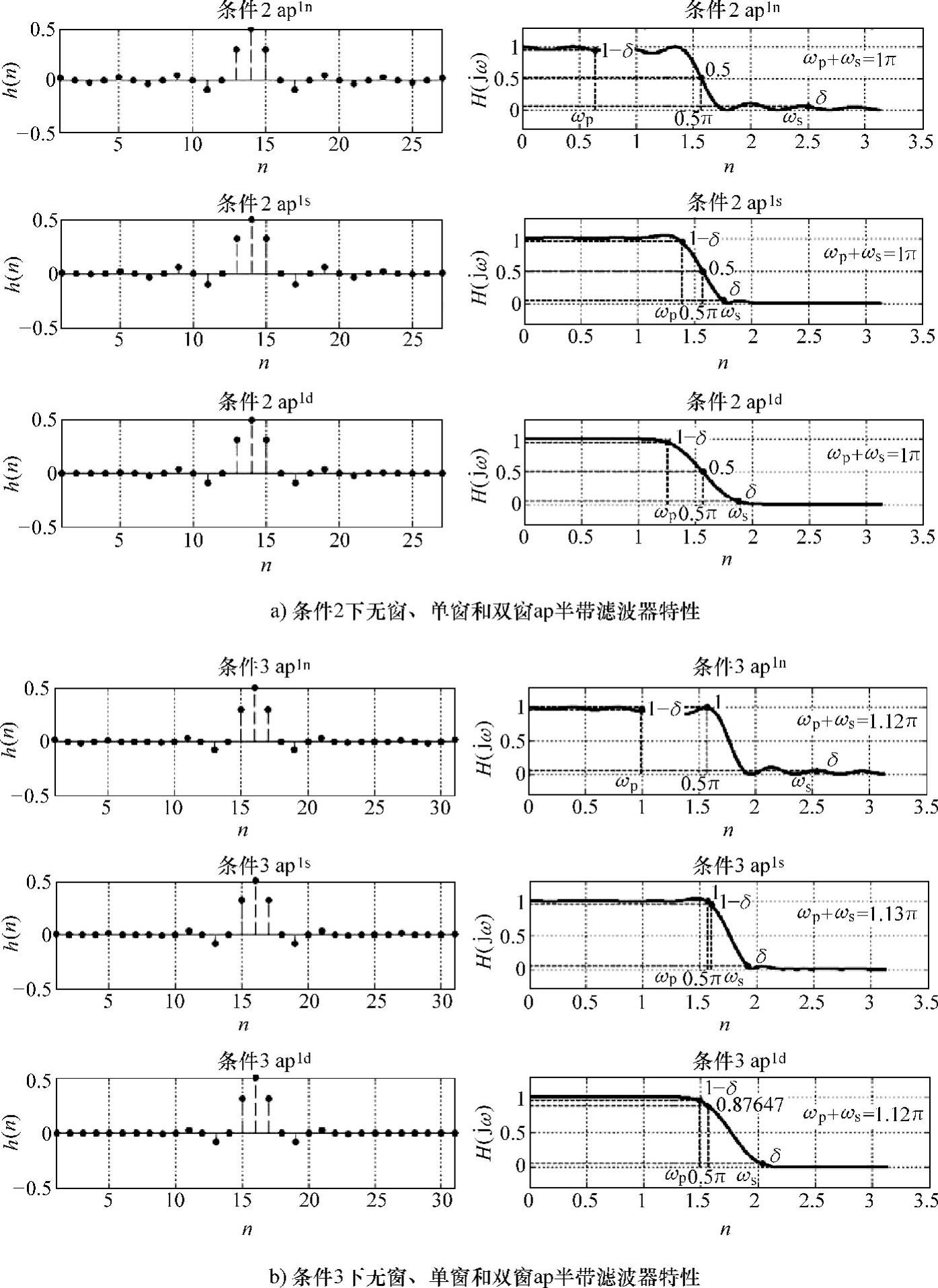
图7-21 满足条件2、3的ap^1nsd半带滤波器

运行结果如图7-21所示。可看出条件2下ap^1nsd半带滤波器均通过了π/2频点，通带和阻带波纹幅度为δ的截止频率ω_p+ω_s=π则证实在整个频带内关于π/2频点奇对称；在条件3下（α=1时）ap^1ns半带滤波器在π/2频点幅值等于1，但对于ap^1d半带滤波器则为0.87467，此结论在第2章中已证明过。ω_p+ω_s>π则说明在条件3下通带和阻带内的波动较条件2下减少。横向对比，ap^1d的平滑性明显好于ap^1ns，但牺牲了带宽。需要指出的是，条件3下ap半带滤波器h（n）是复数，但满足中心共轭对称，因此具有式（7-56）的线性相位特性。图7-21b只画出了其实部。

全相位半带滤波器设计方法

相关推荐