霍尔传感器是比较理想的快速电流、电压信号检测传感器，它的核心器件是霍尔器件。将被检测的电压信号与LEM霍尔电压传感器的一次线圈及检测电阻RI相连接，构成回路，将检测的电压转换为霍尔电压传感器一次线圈的电流，该电流......
2023-06-30
应用W-O谱分析技术进行信号检测优化
【摘要】：为了检测W-O算法对信号检测能力的提高，要对含有噪声的双频正弦波做谱分析。W-O谱提升了信号能量，使邻近噪声谱得到很大程度的压抑。表6-2 二维信号W-O谱检测对比统计结果上面的实验结果验证了频率相近的两个信号通过W-O谱分析后分离度得到增加，便于提取。表6-2 二维信号W-O谱检测对比统计结果图6-13 二维信号W-O谱检测对比图图6-13 二维信号W-O谱检测对比图
为了检测W-O算法对信号检测能力的提高，要对含有噪声的双频正弦波做谱分析。设信号由频率分别为240Hz和248.8Hz，幅值为0.3的正弦波组成，并受均值为0，方差为1的高斯白噪声n（t）干扰，信噪比为-10dB，信号被噪声淹没，即
s（t）=0.3sin（2π·240t）+0.3sin（2π·248.8t）+n（t） （6-32）
采样频率fs=2048Hz，进行长度为512点的FFT仿真结果如图6-12所示（取半边谱图）。
图6-12 一维信号W-O谱检测对比图
传统加矩形窗、三角窗和汉宁窗与apnsd W-O谱检测结果中两个正弦相对幅值及噪声谱统计结果见表6-1。
表6-1 一维信号W-O谱检测对比统计结果
上面的实验结果验证了频率相近的两个信号通过W-O谱分析后分离度得到增加，便于提取。W-O谱提升了信号能量，使邻近噪声谱得到很大程度的压抑。无论从谱均值还是方差来对比，W-O效果均优于传统直接分析法。MATLAB实现代码与上述spWO函数基本相同，不再列出。需要注意是，MATLAB中噪声通过随机函数来生成，其中rand产生的噪声满足均匀分布，randn则是产生满足均值为0和方差为1的正态分布即高斯白噪声。
二维信号W-O谱分析进行信号检测的过程与一维信号类似，假设二维信号s成分中信噪比为-10dB，构成如下：
s=0.3sin（480πtr+497.6πtc）+n（tr，tc） （6-33）
式中，n（tr，tc）是均值为0，方差为1的二维高斯白噪声。采样频率fs=1024Hz，进行长度为64点的二维FFT谱分析，W-O方法与传统加窗方法得到结果对比图如图6-13所示。
统计结果见表6-2。
表6-2 二维信号W-O谱检测对比统计结果
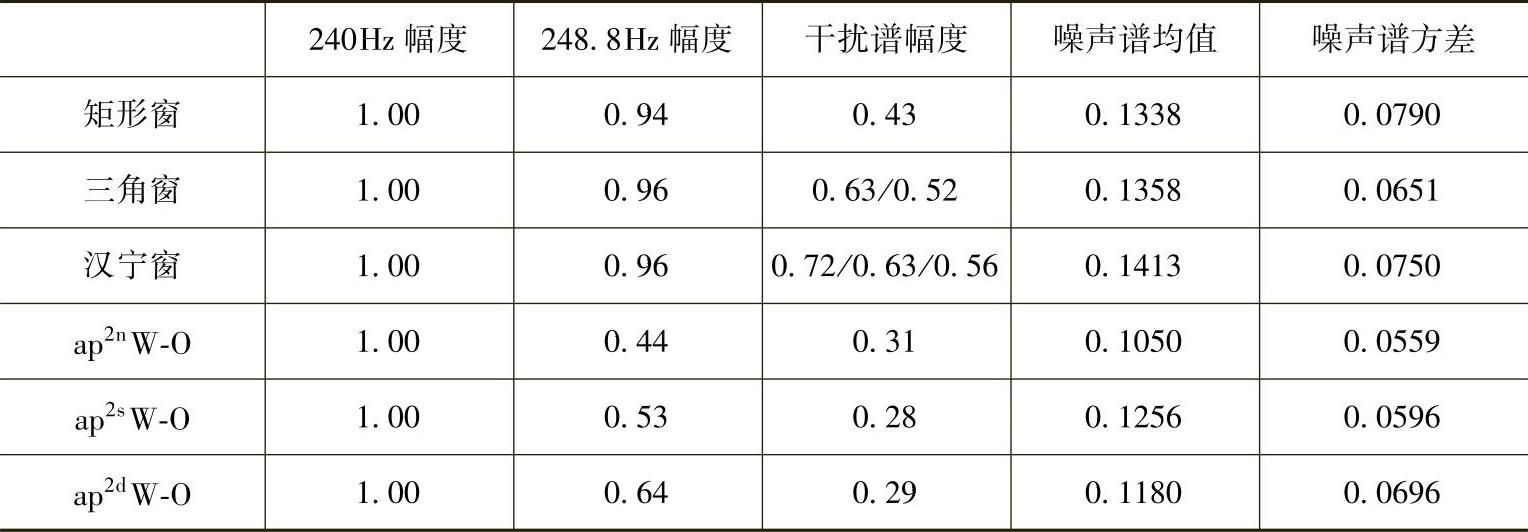
图6-13 二维信号W-O谱检测对比图
有关全相位数字信号处理方法及MATLAB实现的文章
- 详细阅读
-
如何进行热导率检测？详细阅读
影响涂层热导率的因素很多。温度、显微结构、化学成分、孔隙率等都能显著地改变涂层材料的热导率，属组织敏感参量，目前涂层材料的热导率数值多采用实测的方法获得。由式可知，要想得到热导率λ的值，必须首先知道热扩散率a、比定压热容cp以及密度ρ。λ=acpρ 1.热扩散率的测量方法参照GJB1201.1—1991标准，采用非稳态激光脉冲法进行。......
2023-06-18
-
电致发光谱分析技术优化方案详细阅读
与光致发光不同的地方在于激发的手段,光致发光是光激发,而电致发光是通过电场激发。图2.5.3电致发光谱的光路示意图2.电致发光谱的测量装置如图2.5.3所示,电致发光谱的测量装置与光致发光谱相似,不同点在于激发源的不同,分光系统、样品室以及探测和数据记录系统与光致发光谱装置基本相同。......
2023-06-23
-
紫外光谱分析技术优化方法详细阅读
图2.2.22-en 与dsDNA 相互作用的紫外吸收光谱图图2.2.2为5.0×10-5mol/L2-en与不同量dsDNA相互作用的紫外吸收光谱图。当在配合物溶液中加入不同量dsDNA后，配合物特征吸收峰出现了不同程度的减色效应，且在324 nm处出现一个等吸收点，表明二者发生相互作用，生成了新的复合物。另一方面，Fc单体是众所周知的沟槽结合配体，因此我们猜测2-en与dsDNA以沟槽结合模式相互作用。......
2023-06-22
-
使用装配孔定位技术进行优化详细阅读
图6-8翼肋组合件装配孔的加工和协调路线示意图装配孔定位的准确度取决于装配孔的协调方法。另外，为减少划线工作量，一般是将装配孔和导孔联合使用，即导孔一装配孔方法。此时按蒙皮上预先已钻制好的装配孔来定位固定其他零件。图6-9以装配孔定位的壁板装配型架示意图1—蒙皮；2—托板；3—工艺螺钉点焊和胶结结构的板件也可采用装配孔定位。......
2023-07-18
-
理解视觉检测技术原理与应用详细阅读
视觉检测采用图像传感器实现对被测物体的尺寸及空间位姿的三维非接触测量。图1给出了基于三角法的主动视觉测量原理，即结构光传感器测量原理。视觉检测技术的应用非常灵活，能适用于不同类型的检测任务[5，6]。视觉检测系统原理如图3所示。全局标定是多传感器视觉检测系统的关键技术和难点，已经取得的研究成果成功地解决了这一难题，实现了视觉检测系统的现场全局标定[7]，使视觉检测技术走向成熟和实用。......
2023-06-23
-
直播卫星信号监测技术优化探讨详细阅读
开展广播电视村村通直播卫星节目接收信号监测工作，对推动广播电视村村通工程的健康发展，提升直播卫星覆盖工程的科学化管理水平，构建广播电视公共服务体系长效运行机制，保障直播卫星覆盖工程受益群众收听收看权益等具有十分重要的意义。......
2023-06-24
-
果对圆锥滚子轴承套圈的检测原理进行优化详细阅读
图7-62 圆锥滚子轴承套圈结构及其待检测部位2）发纹：材料表面或近表面毛发状的细小裂纹，由钢锭皮下气泡或夹杂引起。然而在实际检测过程中，使得轴承套圈各个部分均达到饱和磁化状态需要极多的线圈匝数或极大的磁化电流，对于非定量轴承套圈检测而言，磁化的意义在于使得最苛刻指标的缺陷仍可得到较理想的信噪比即可，磁化效......
2023-06-22
相关推荐