【摘要】:对于双窗系统,EN不再恒等于1,但具有“倒余弦”形状,这样W-O分析谱中在每点都产生旁瓣。同古典谱估计方法相比,由于AR模型是一个有理分式,因而估计出的谱比古典谱估计法估计出的谱平滑。由式易知,X0在k=0时的权值为N,即阶数越高,W-O谱线分辨力越强。图6-9 传统信号加窗与W-O谱分析由图6-9可以看出,用W-O方法得到的信号频谱比用传统加窗方法具有更少、更低的旁瓣干扰。
用W-O方法分析信号频谱是对W-O处理后的信号做傅里叶变换,这相当于信号首先经过一个线性系统W-O,如图6-7所示。
N阶全相滤波器的输入矢量x是2N-1阶的,图6-7中的输出等于x′与延迟窗C相乘后并重叠,即x′形式如下:
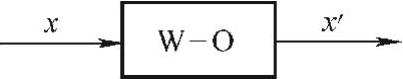
图6-7 谱分析中的W-O模型
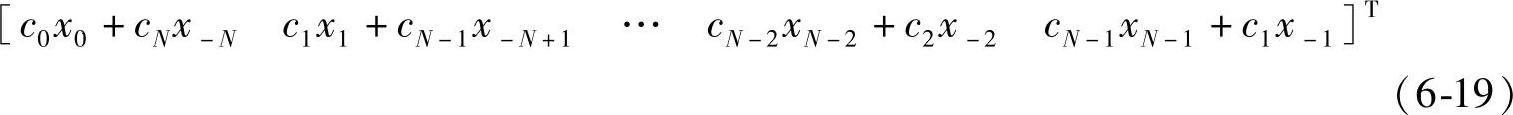
设x′=x0′+x1′,其中
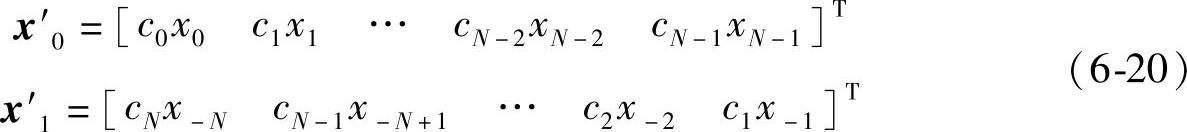
由式(6-20)得到W-O模型的输出x′频谱如下:
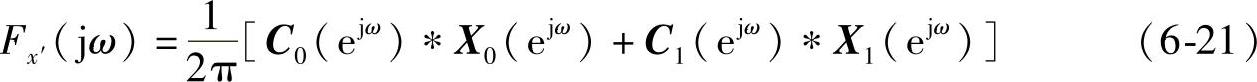
式中,C0和C1分别定义如下:
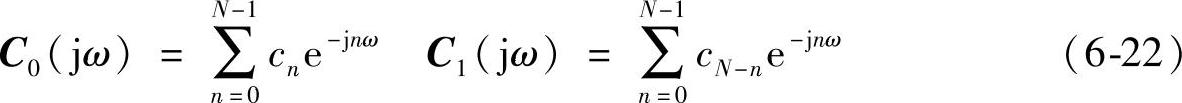
分析具有单一频率ω0的正弦信号的频谱,所以式(6-21)中两分量的频谱分别为
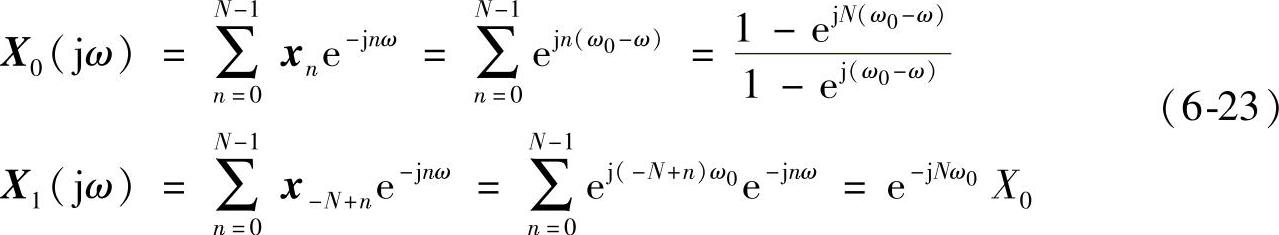
将式(6-21)代入式(6-23)得到:
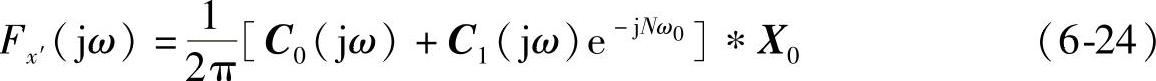
由式(6-23)可以看出X0就是经典频谱分析中信号加矩形窗时的频谱,因此式(6-24)给出了经过W-O处理后信号x′频谱与原信号频谱x之间的关系。由数字信号处理基础理论可知,实际上在采用DFT对长度为N的截断信号进行谱计算时,X0只有在ω=ω0+2kπ/N处的值正确,而采用DFT计算得到的各点频谱等于X0在2nπ/N(0≤n≤N-1)处的抽样。即只有当ω0=2mπ/N(m=n-k)时运用DFT才得到正确的谱分析结果,频谱为在m处一个冲击(半个周期内)。由式(6-24)可得对应x′频谱如下:
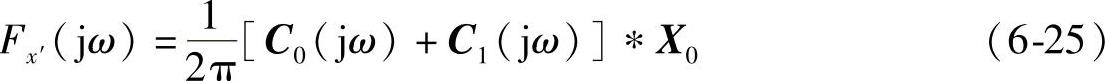
对于单窗和无窗系统,由第2章中的内容可知其频偏向量EN恒等于1,所以结合式(6-22)和式(6-25)可得到ω=ω0时x′频谱为

即在各点处的频谱N/2π倍于原信号频谱且未发生非线性转换,所以当N≥8时x′频谱将得到加强。对于双窗系统,EN不再恒等于1,但具有“倒余弦”形状,这样W-O分析谱中在每点都产生旁瓣。由式(6-26)易知,这种“倒余弦”与X0卷积的结果仍然保持了较大的主旁边能量比。
当ω0=2π(m+θ)/N(0<θ<1)时,代入式(6-26)可得
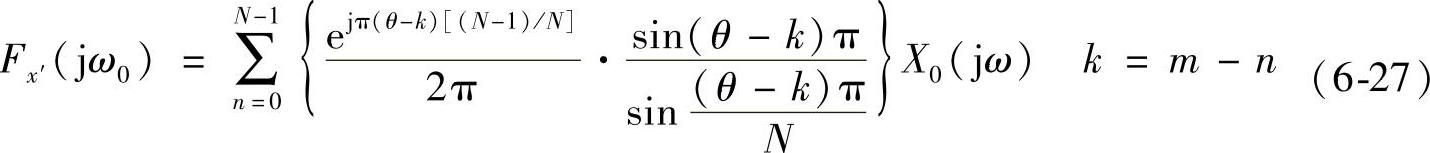
由式(6-27)可以看出,由于非整数倍θ的存在,使x′在任意点的频谱都由原信号频谱全体通过加权得到,其权值函数sin(·)/sin(·/N)的曲线具有突出主瓣且通过平均弱化旁瓣的特性。如N=32,θ=0.3,k由0变化到N-1时对应的曲线如图6-8所示。
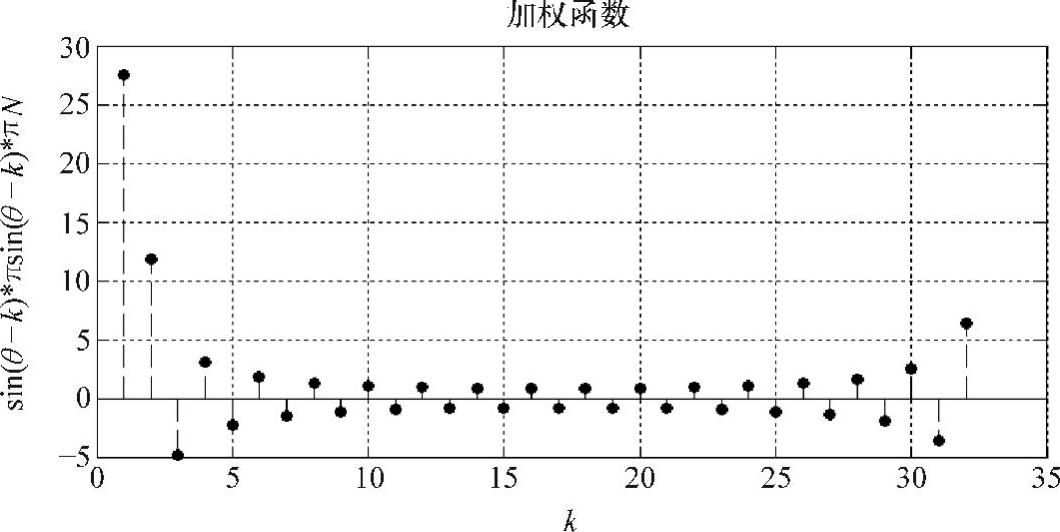
由图6-8可以看出,当k=0时即n=m具有最大值,其余各点的权值有正有负而弱化了旁瓣的影响,使ω=2πm/N时谱线相对能量更大。由式(6-27)易知,X0在k=0时的权值为N,即阶数越高,W-O谱线分辨力越强。如对频率f0=12.3Hz的正弦信号以抽样频率fs=32Hz进行抽样并作N=32的FFT谱分析,
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
图6-8 加权函数曲线
W-O方法与传统加窗方法得到结果对比图如图6-9所示。
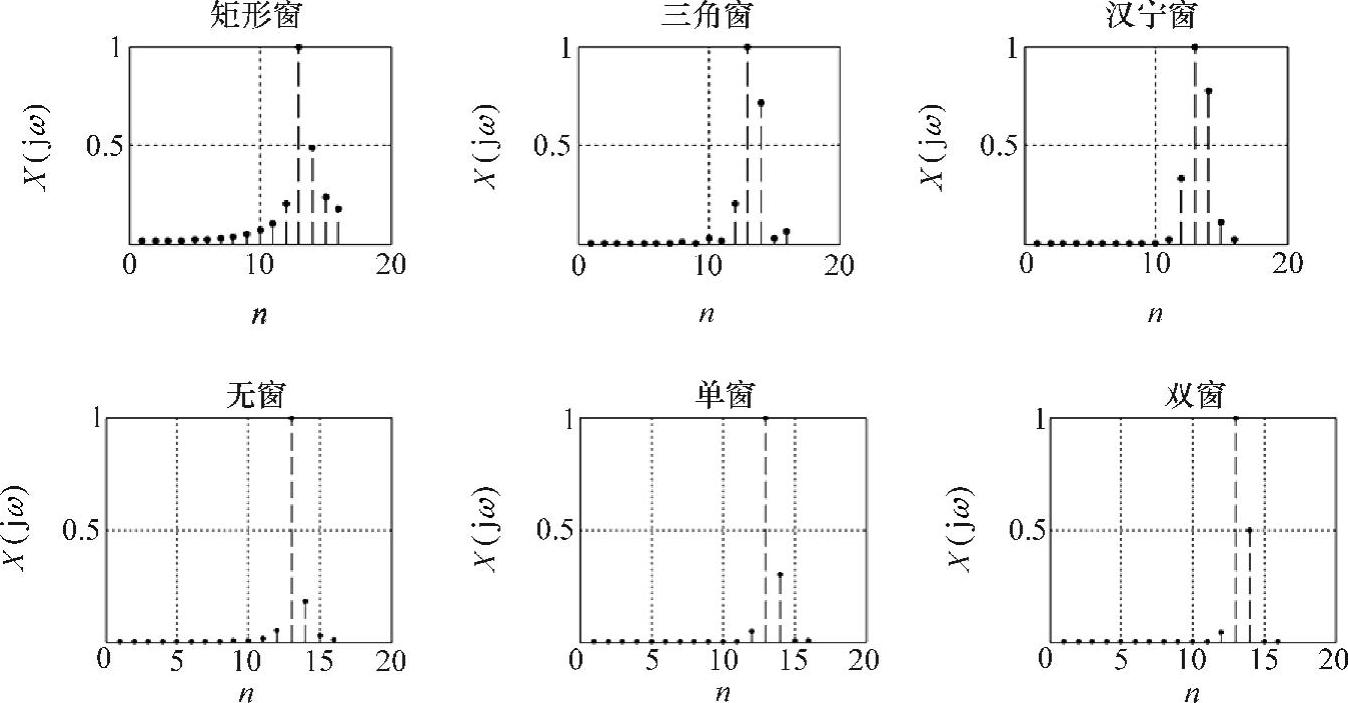
图6-9 传统信号加窗与W-O谱分析
由图6-9可以看出,用W-O方法得到的信号频谱比用传统加窗方法具有更少、更低的旁瓣干扰。在无窗、单窗和双窗W-O分析中,双窗得到的频谱旁瓣最少,但第一旁瓣的干扰比无窗和单窗大而且对于整数倍单频的信号双窗W-O得到的频谱也有旁瓣。单窗比无窗W-O得到的信号频谱有较少的旁瓣但第一旁瓣干扰也较大。实现上面结果的MATLAB代码如下:


二维信号的W-O处理如图5-26所示,如果选择的卷积窗满足完全对称(即水平方向、垂直方向和中心都对称),则二维全相位W-O处理输出等于输入与C的卷积,从而有如下关系:
x′=xC⇒Fx′(jωr,jωc)=FC(jωr,jωc)·X0(jωr,jωc) (6-28)
对于ap2 n,卷积窗C的谱等于前后矩形基窗的乘积,容易推导得到:
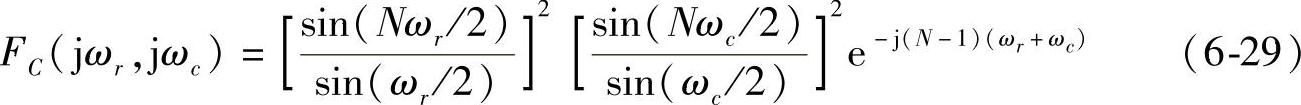
结合式(6-28)和式(6-29),得到ap2n的W-O处理输出谱为
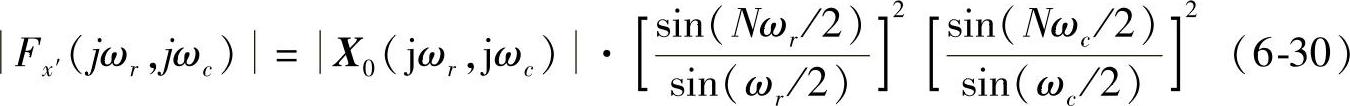
同一维结论相似,二维权值函数的曲线在行列方向上均具有突出主瓣且通过平均弱化旁瓣的特性。如N=32的均匀取样得到的加权函数曲面如图6-10所示。
由曲面形状及式(6-30)可知,x′谱线幅值是x在行列方向上的权值函数平方。主瓣的权值最大而旁瓣的权值按照平方关系快速衰减,这使x′谱线主瓣更加突出,所以W-O处理具有很好的抑制谱泄露特性。抑制效果与卷积窗形状密切相关,一种直观的改善方法是提高sin(N·)/sin(·)的幂次。可通过两种途径来实现,其一是卷积窗形状,采用可分离基窗直接相乘得到二维基窗是常用的简易方法,生成的二维窗性质与一维基窗相同,但这种方法没有把行列方向上的互相关性考虑进去,因此,同时以行、列及±45°等方向上按照某种准则设计二维窗是值得探究的内容。其二是采用ap2sd方式进行W-O处理,在阶数相同条件下,幂次将分别提高1和2。
设二维信号由频率fr=12.3Hz和fc=21.6Hz的正弦信号组成且初相为零,即
s=sin(2πfrtr+2πfctc) (6-31)
以抽样频率fs=64Hz进行抽样并作N=32的FFT谱分析,W-O方法与传统加窗方法得到结果对比图如图6-11所示。
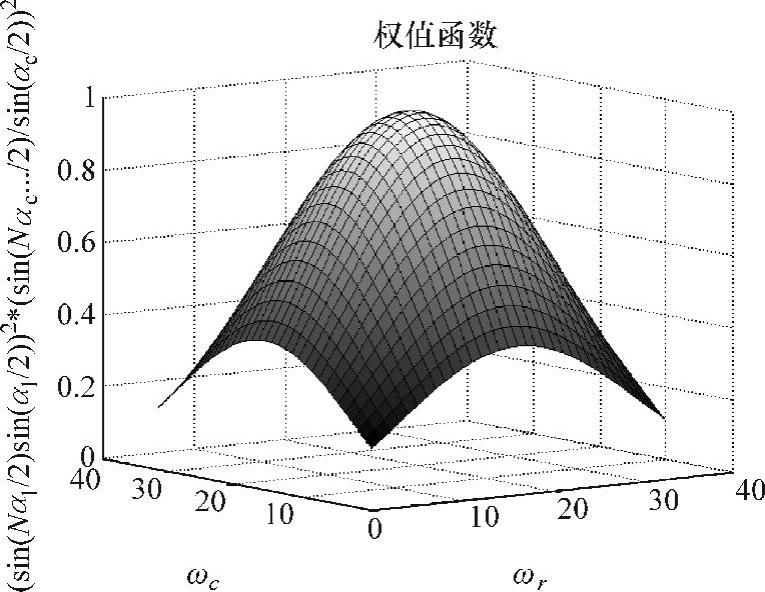
图6-10 二维W-O权值函数曲面
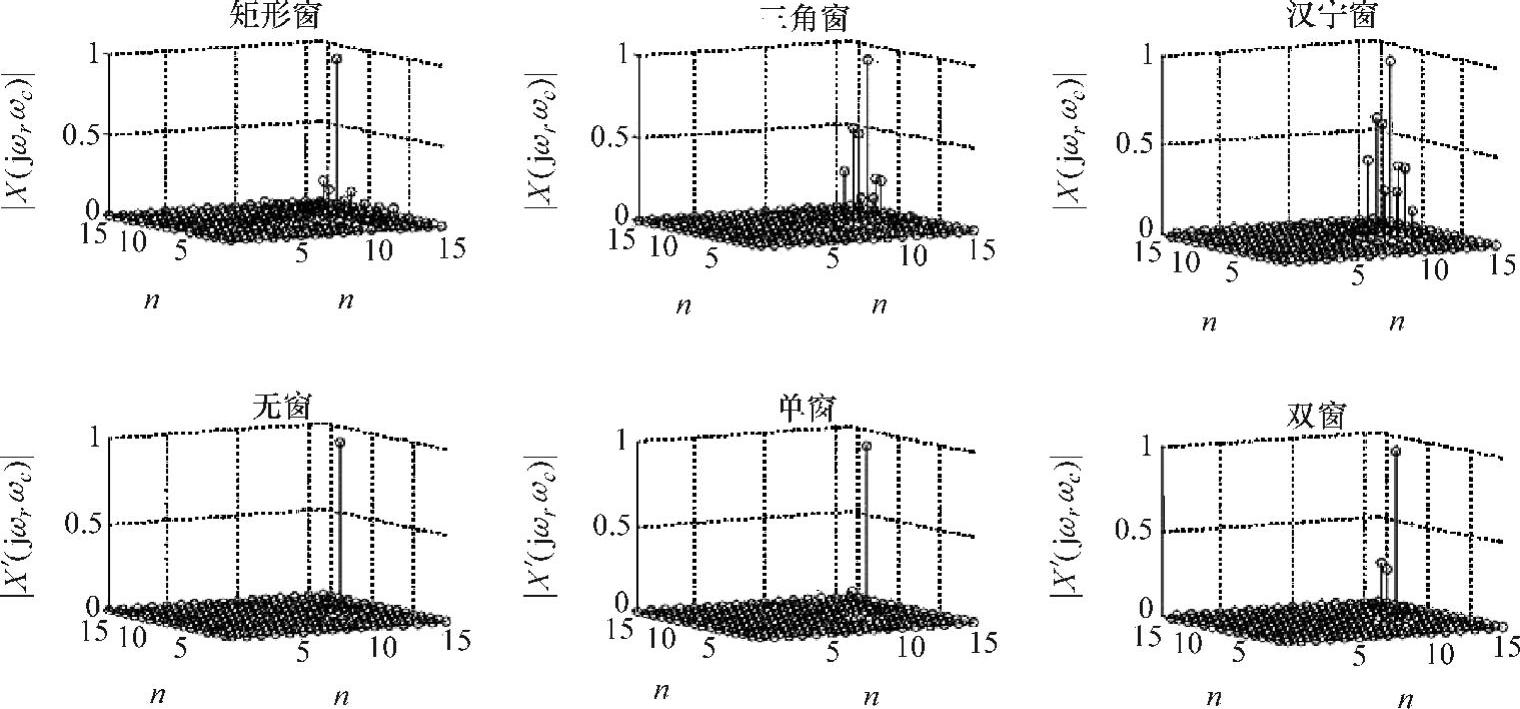
图6-11 二维信号W-O谱分析结果对比
实现上述结果的MATLAB代码如下:


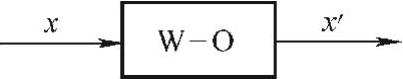
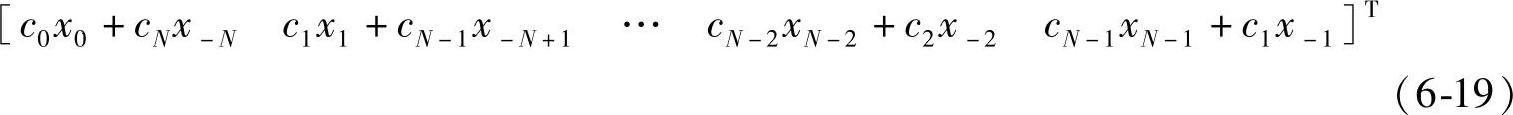
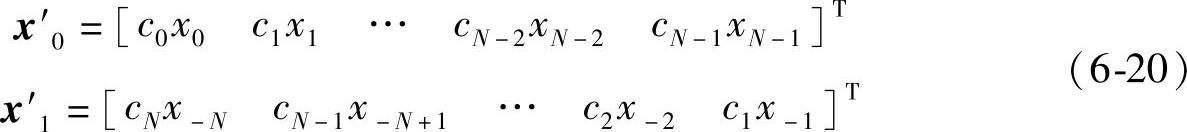
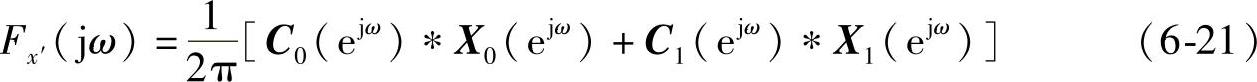
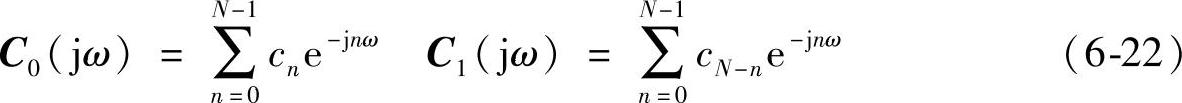
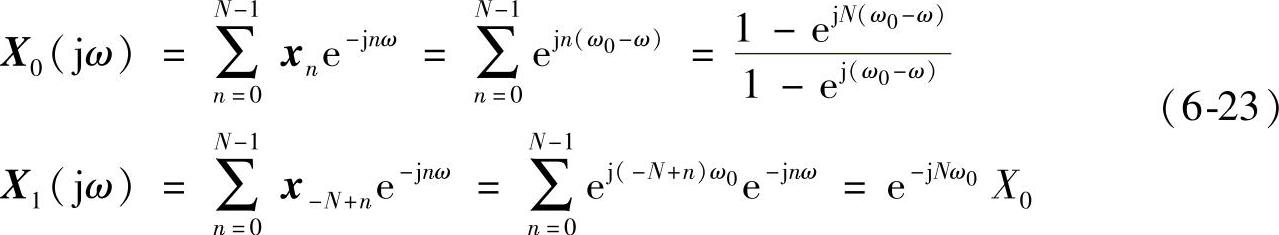
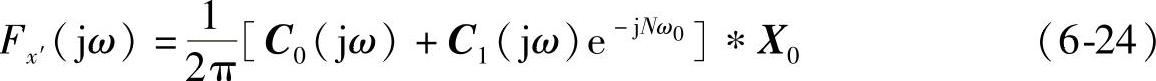
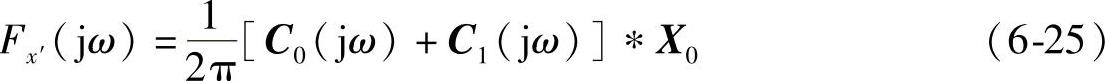

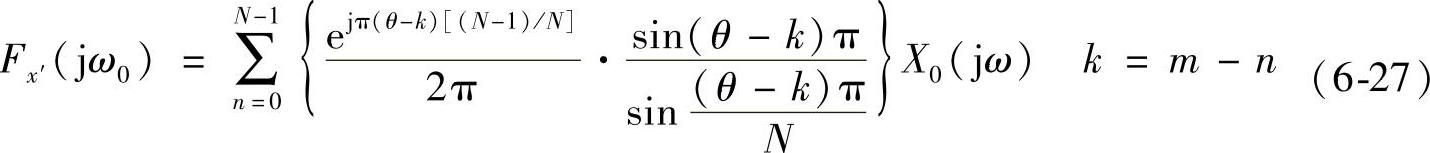
 (https://www.chuimin.cn)
(https://www.chuimin.cn)


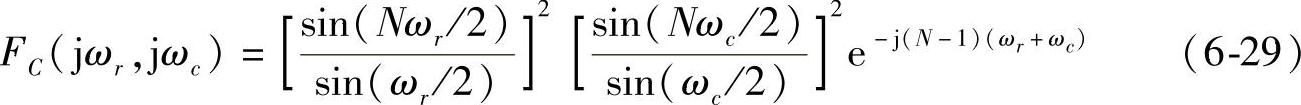
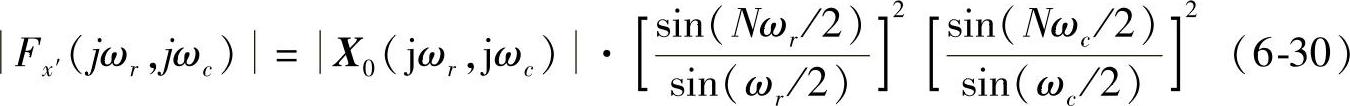










相关推荐