系统原理同图2-26所示,对应的输出为式中式中Tk的表达式与apDCT时相同。此外,apDWT具有与apDCT相同的传输特性函数形式,因此也具有严格零相位的特性。图4-11 基于apDWT子带分解信号图实际上,不论是何种正交变换,按照全相位信号处理方法得到的ap都可以对信号进行去除分段效应的滤波和处理,它是建立在新概念上的一种滤波系统。......
2025-09-29
对于二维余弦变换,α=C,β=CT,代入到式(5-64)并简单整理可得:
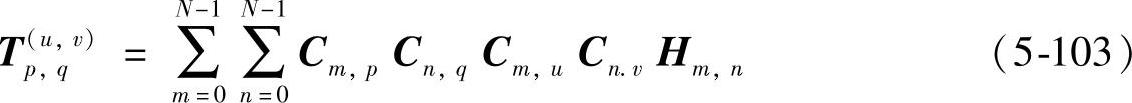
相乘的四个余弦基元素不能进一步合并,所以余弦全相位核没有更具体的表达形式。对于二维沃尔什变换,α=WN,β=α,代入到式(5-64)并简单整理可得:
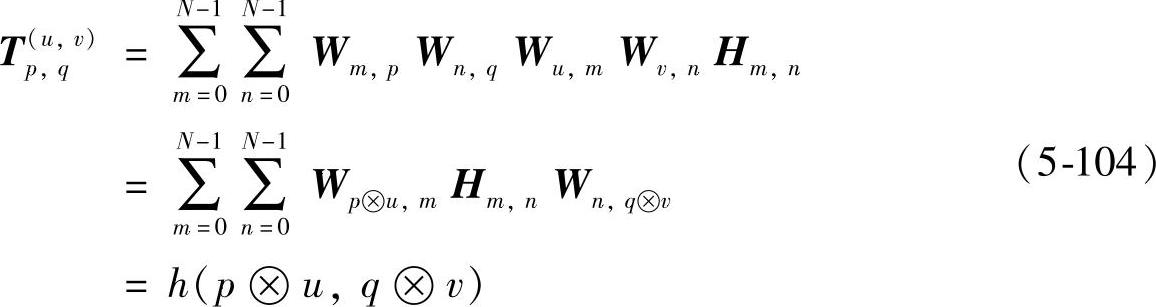
式(5-104)中符号 表示异或运算。对于ap2 DCT的全相位变换核,有
表示异或运算。对于ap2 DCT的全相位变换核,有
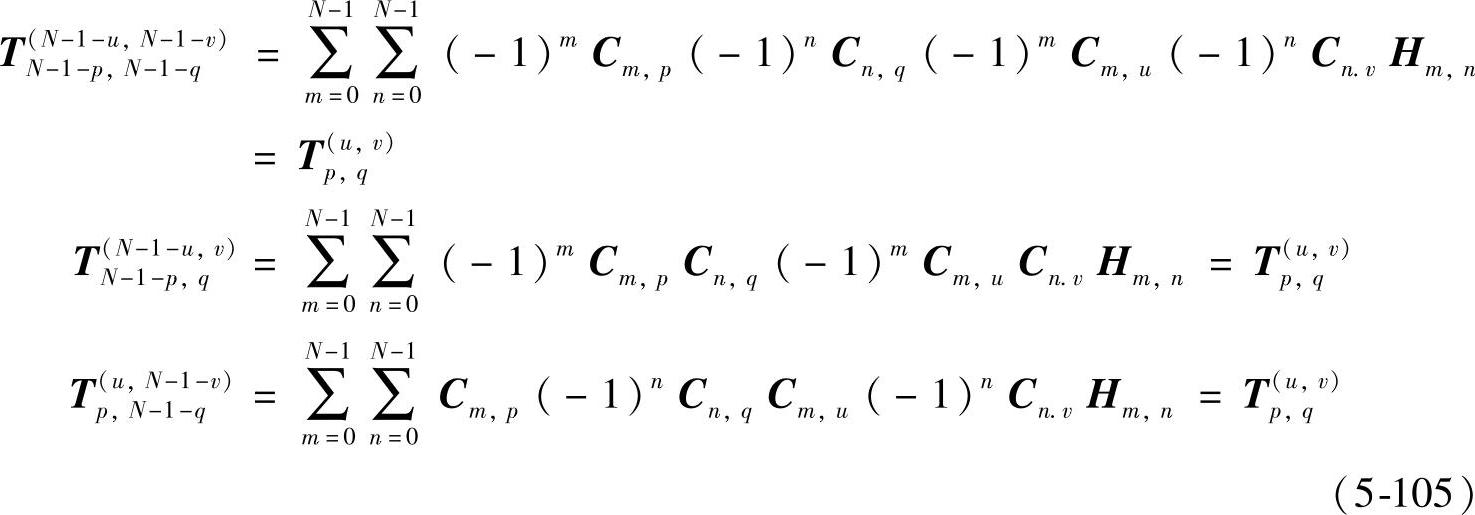
当N是2的整数幂时,p u=(N-1-p)
u=(N-1-p) (N-1-u),所以式(5-105)的结论对二维apDWT的核仍然成立。基于此结论的ap2 DCT和ap2 DWT的全相位变换基也具有对称性。根据式(5-94)的定义,位于第四象限的A—元素Ar,c的中心对称是位于第一象限的A++的元素A-r,-c,两者的关系(假定双基窗均经过归一化处理)推导如下:
(N-1-u),所以式(5-105)的结论对二维apDWT的核仍然成立。基于此结论的ap2 DCT和ap2 DWT的全相位变换基也具有对称性。根据式(5-94)的定义,位于第四象限的A—元素Ar,c的中心对称是位于第一象限的A++的元素A-r,-c,两者的关系(假定双基窗均经过归一化处理)推导如下:
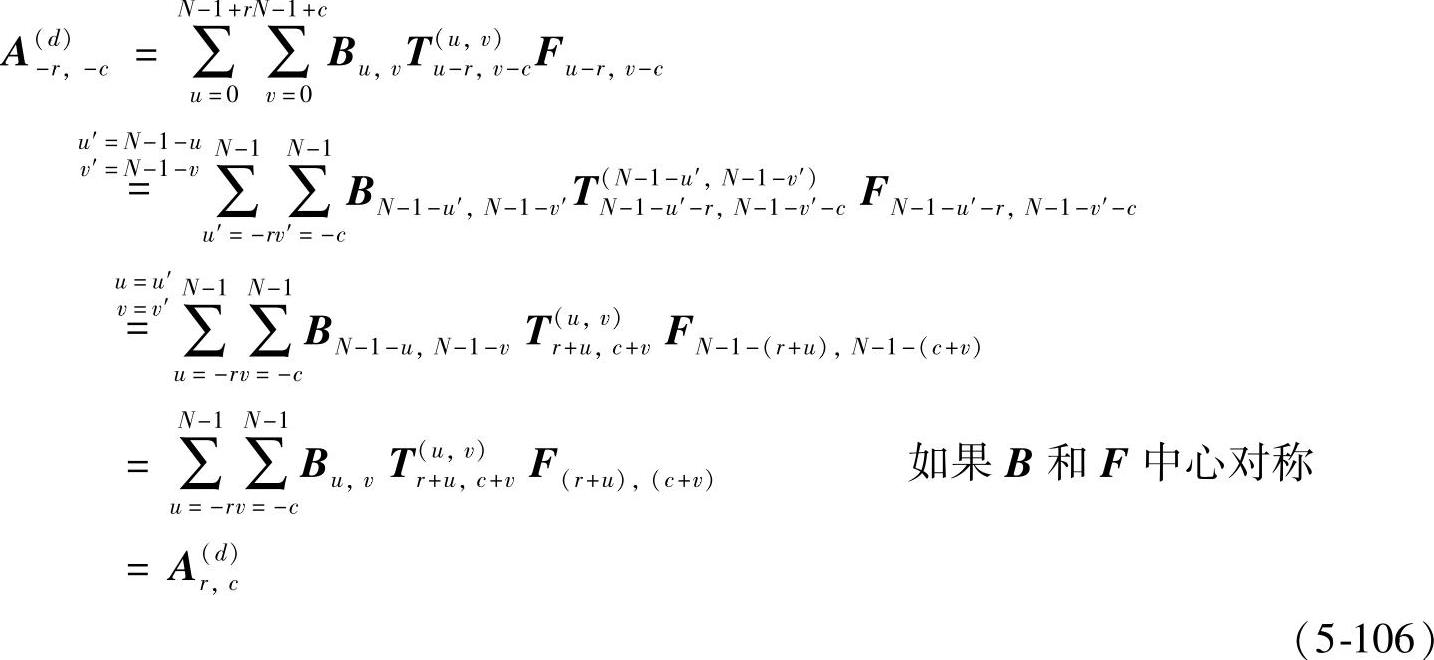
式(5-106)成立的条件只是要求基窗具有中心对称性,即对于任意传输矩阵H,全相位处理的特性都具有严格零相位。同样可证明,当前后基窗分别具有水平和垂直对称性时,全相位基又满足如下:
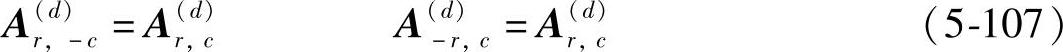
对于第四象限的A—元素Ar,c的转置,可推导出如下结论:
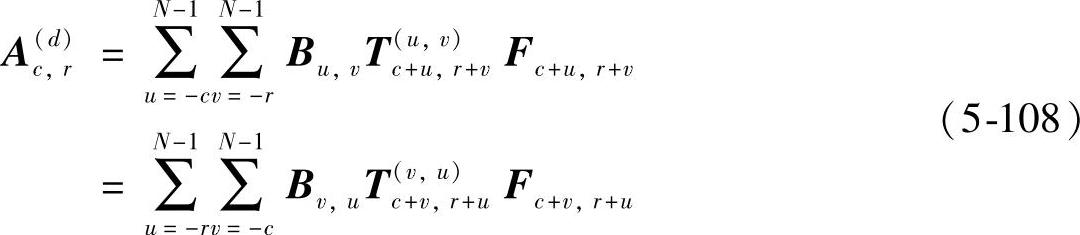
当前后基窗满足主对称性,且全相位核满足如下条件时,Ar,c也具有了主对称性。

结合式(5-103),若式(5-109)成立,则有
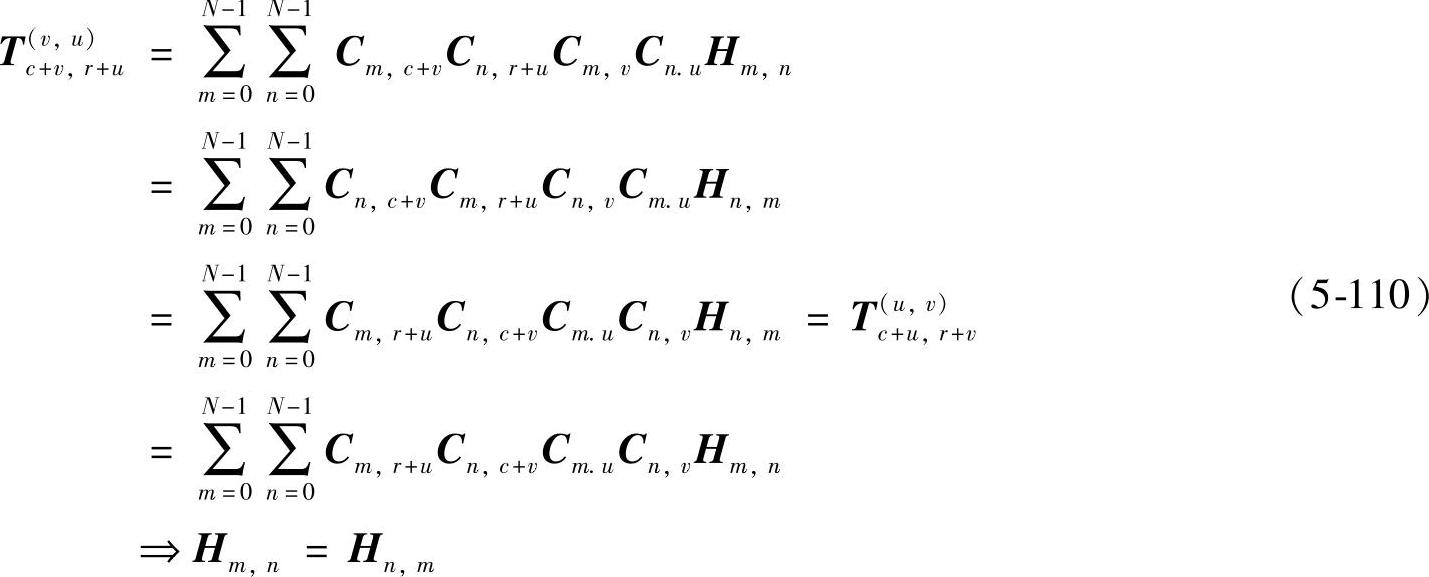
对于二维apDWT,则有
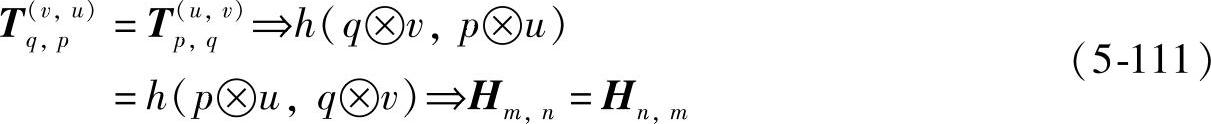
综合以上,对于ap2d DCT和ap2d DWT,我们有如下结论:
1)当前基窗F和后基窗B具有中心对称性时,全相位基中心对称;(https://www.chuimin.cn)
2)当前后基窗水平/垂直对称时,全相位基水平/垂直对称;
3)当前后基窗和传输矩阵H主对称时,全相位基满足主对称性;
在对二维信号进行全相位处理时,基窗的选择和H的设定是必须考虑的问题。如果认为其他像素与中心像素的相关性与距离成反比且各向同性,则基窗应定义为中心各向对称,即同时满足水平、垂直、中心和主对称。根据信号相关性分布方向来自适应设置基窗以达到一定条件下的最优全相位信号处理效果是值得研究的内容。对于H的定义,则与处理的目标任务相关,即由在各个方向上不同列率信号分量的取舍来决定。如果行列上情形相同,则H具有主对称性。下面的讨论中,除非特别指出,前后基窗相等且具有中心各向对称性,H也满足主对称性。假设H定义如下:

以图5-20给出的3种卷基窗分别形成的二维apDCT传输特性如图5-21所示。
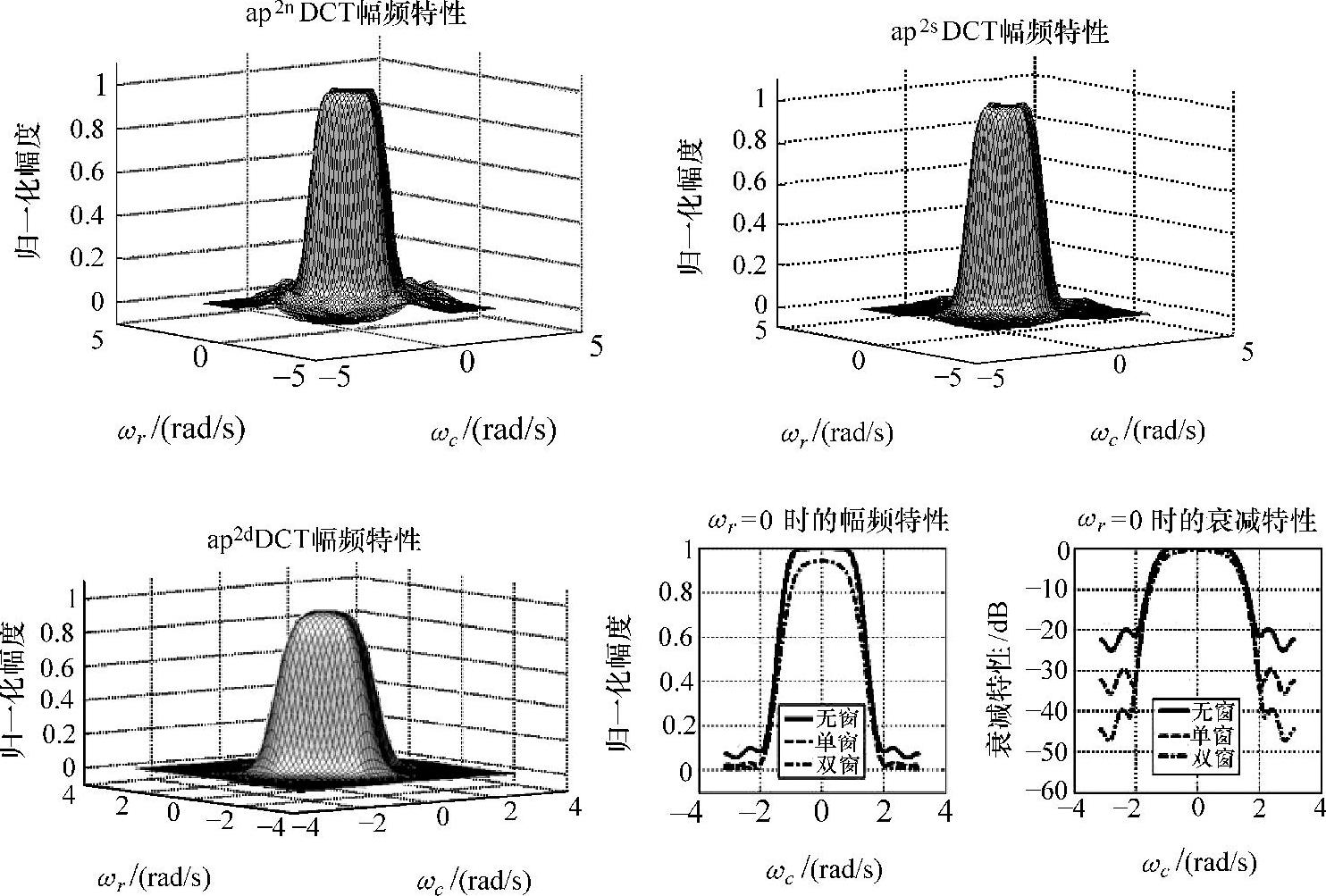
图5-21 ap2nsd DCT特性曲面及曲线图
从图中可看出apDCT的平滑性好于apDFT,ap2d DCT的衰减特性比ap2n DCT低20dB,但由于采用与ap2n DCT和ap2s DCT相同的归一化条件,峰值幅度低于1且过渡带宽度增大。相比而言,ap2s DCT在衰减特性和过渡带宽度都表现出良好特性。生成图5-21所述功能的MATLAB代码(只列出与ap2nsd DFT不同的部分)如下:


与上相同条件形成的二维ap2nsd DWT传输特性如图5-22所示。
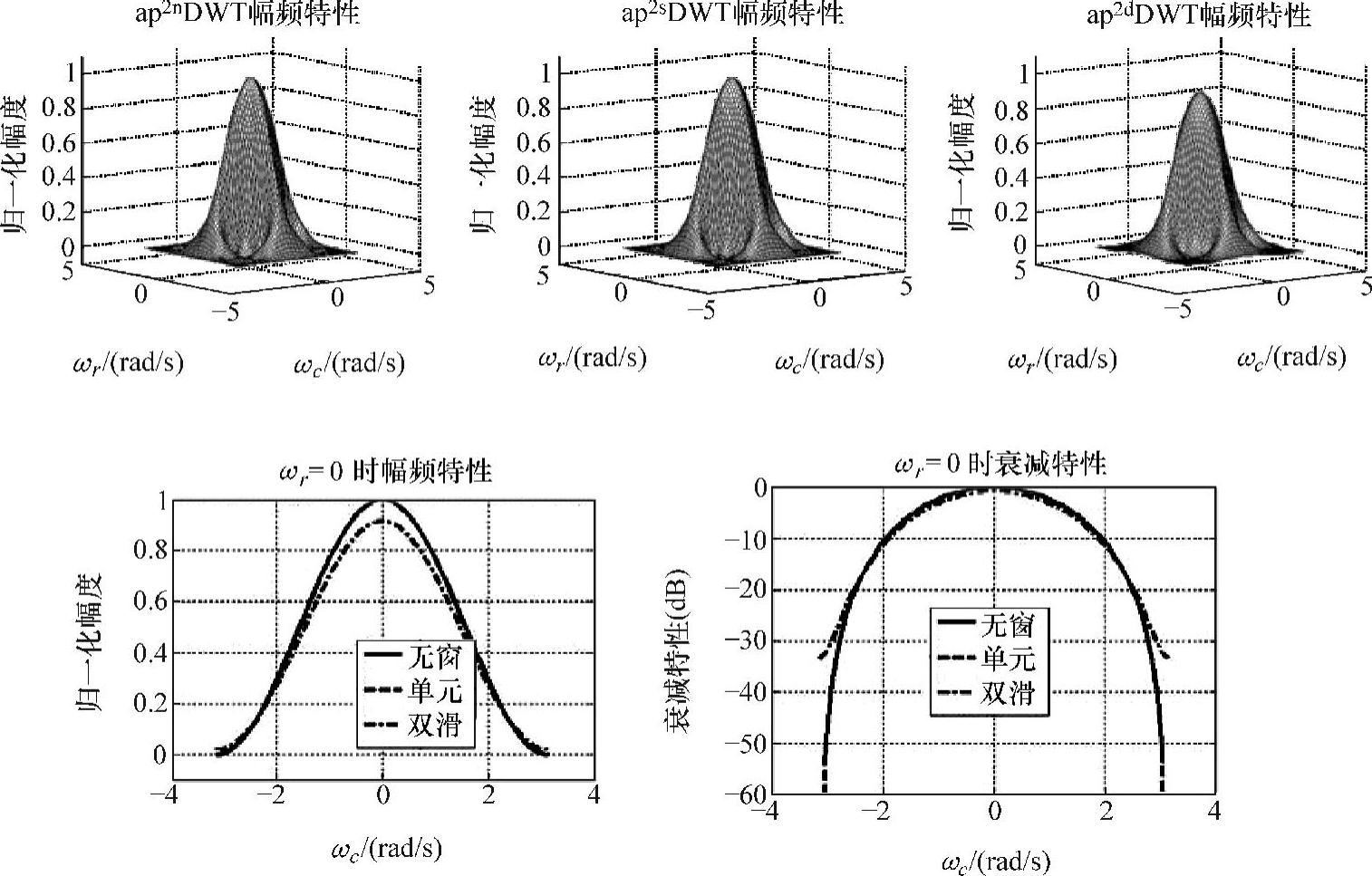
图5-22 ap2nsd DWT特性曲面及曲线图
生成图5-22结果的MATLAB代码与ap2nsd DCT只有函数getA不同,具体如下:


上面给出了DCT和DWT变换情况下设计二维全相信号处理基本方法,虽然特性曲面物理意义不如DFT直接,即通过H来定义的传输特性不能与曲面特征建立直接对应关系,但提供了信号处理新思路,且具有严格零相位和优良平滑性等特点。
相关文章

系统原理同图2-26所示,对应的输出为式中式中Tk的表达式与apDCT时相同。此外,apDWT具有与apDCT相同的传输特性函数形式,因此也具有严格零相位的特性。图4-11 基于apDWT子带分解信号图实际上,不论是何种正交变换,按照全相位信号处理方法得到的ap都可以对信号进行去除分段效应的滤波和处理,它是建立在新概念上的一种滤波系统。......
2025-09-29

国际标准建议CCITT H.261、JPEG、MPEG中都采用8×8的块做DCT,但基于DCT的数字滤波尚不普遍。为使DCT所具有的优良特性能在数字滤波中得到充分发挥,结合全相滤波的概念提出了DCT域ap系统设计。TN-2TN-1],其传输特性为显然,apDCT具有严格零相位。实现无窗、单窗和双窗apDCT与传统滤波器特性的MATLAB代码如下:显然,apDCT具有严格零相位。利用apDCT的各子带滤波器对图像的一行进行子带滤波的结果如图4-8所示。......
2025-09-29

沃尔什基矩阵与一维变换时相同,由沃尔什函数产生。由沃尔什矩阵可以构成二维沃尔什函数的基本图像。表5-24 阶沃尔什基本图像矩阵与傅里叶基本图像不同的是,沃尔什变换等其他正交变换基图像均是实矩阵。二维哈达玛变换基矩阵与沃尔什基矩阵只是行向量排列顺序不同,正反变换形式相同。......
2025-09-29

王兆华教授首次给出了无窗、单窗和双窗全相位滤波器的结构形式及其频率特性图;其提出的“全相位FFT谱分析”极大地抑制了频谱泄漏,所有这些奠定了全相位滤波的理论基础。至2001年以来,王兆华教授和侯正信教授指导多名研究生不断丰富全相位滤波的理论并挖掘在多个领域的应用。此外,全相位滤波理论也在通信、语音信号处理、信号重构等方面得到了应用。......
2025-09-29

LED的封闭技术就是对其芯片和两个电极进行保护的技术。LED封装技术大都是在半导体分立器件封装技术基础上发展与演变而来的。图3-22 LED封装工艺流程下面介绍几种常用的封闭技术。具体而言,大功率LED封装的关键技术包括以下几个方面。......
2025-09-29

为降低或解决截断误差,国内外有些专家和学者提出了一些改善措施。设输入数据段长度为N1,系统响应长度为N2。全相位滤波法则是使用最大重叠的新方法,它考虑了对某个输入样本的所有长度为N的分段情况,如图1-7所示。图1-6 理想低通滤波器加矩形窗重叠法是由Malvar等人在DCT基础上提出的解决“方块效应”的方法。......
2025-09-29

图4-12 变换域信号处理图对于N阶系统,时刻n输入xn=[x,x(n-1),…其中X1是1维N阶全相位输入信号,即式就是全相位数字信号处理得到的输出与输入的数学关系表达。把式称为全相位变换,矩阵A称为全相位变换基,矩阵T则为全相位变换核。综合以上,变换域全相位数字信号处理一种可能实现如图4-16所示。......
2025-09-29

如图G8.2所示,水库与下游防护地区之间的区间洪水不可忽略,当发生洪水时,水库仅能控制的是入库洪水,因此,为满足防护地区的防洪要求,水库要考虑区间来水大小,进行补偿放水,这种调节洪水的方式称为防洪补偿调节。图G8.2水库与防洪控制点位置示意图设水库A的泄流到防洪控制点B的传播时间为tAB,区间洪水到防洪控制点B的传播时间为tCB。式、式未考虑区间洪水经河槽调节所导致的流量变化。......
2025-09-29
相关推荐