首页理论教育二维沃尔什和哈达玛变换详解

二维沃尔什和哈达玛变换详解

2023-06-23 理论教育版权反馈

【摘要】：沃尔什基矩阵与一维变换时相同，由沃尔什函数产生。由沃尔什矩阵可以构成二维沃尔什函数的基本图像。表5-24 阶沃尔什基本图像矩阵与傅里叶基本图像不同的是，沃尔什变换等其他正交变换基图像均是实矩阵。二维哈达玛变换基矩阵与沃尔什基矩阵只是行向量排列顺序不同，正反变换形式相同。

对于一个N×N元素组成的图像信号矩阵X，其二维沃尔什变换定义为

T_W=W_NXW_N （5-49）

反变换基与正变换基相同。沃尔什基矩阵与一维变换时相同，由沃尔什函数产生。由沃尔什矩阵可以构成二维沃尔什函数的基本图像。具体方法为：以基矩阵W_N的各行作为图像的一条边，以矩阵的各列作为图像的另一边，分别相乘即可得到N²的沃尔什基本图像。如以N=4为例，4阶沃尔什基本图像X轴方向的4条边分别为[1 1 1 1]，[1 1-1-1]，[1-1-1 1]，[1-1 1-1]；因为基矩阵具有主对称性质，所以Y轴方向4条边与X轴相同，相乘即得到16个沃尔什基本图像，对应矩阵见表5-2。

表5-24 阶沃尔什基本图像矩阵

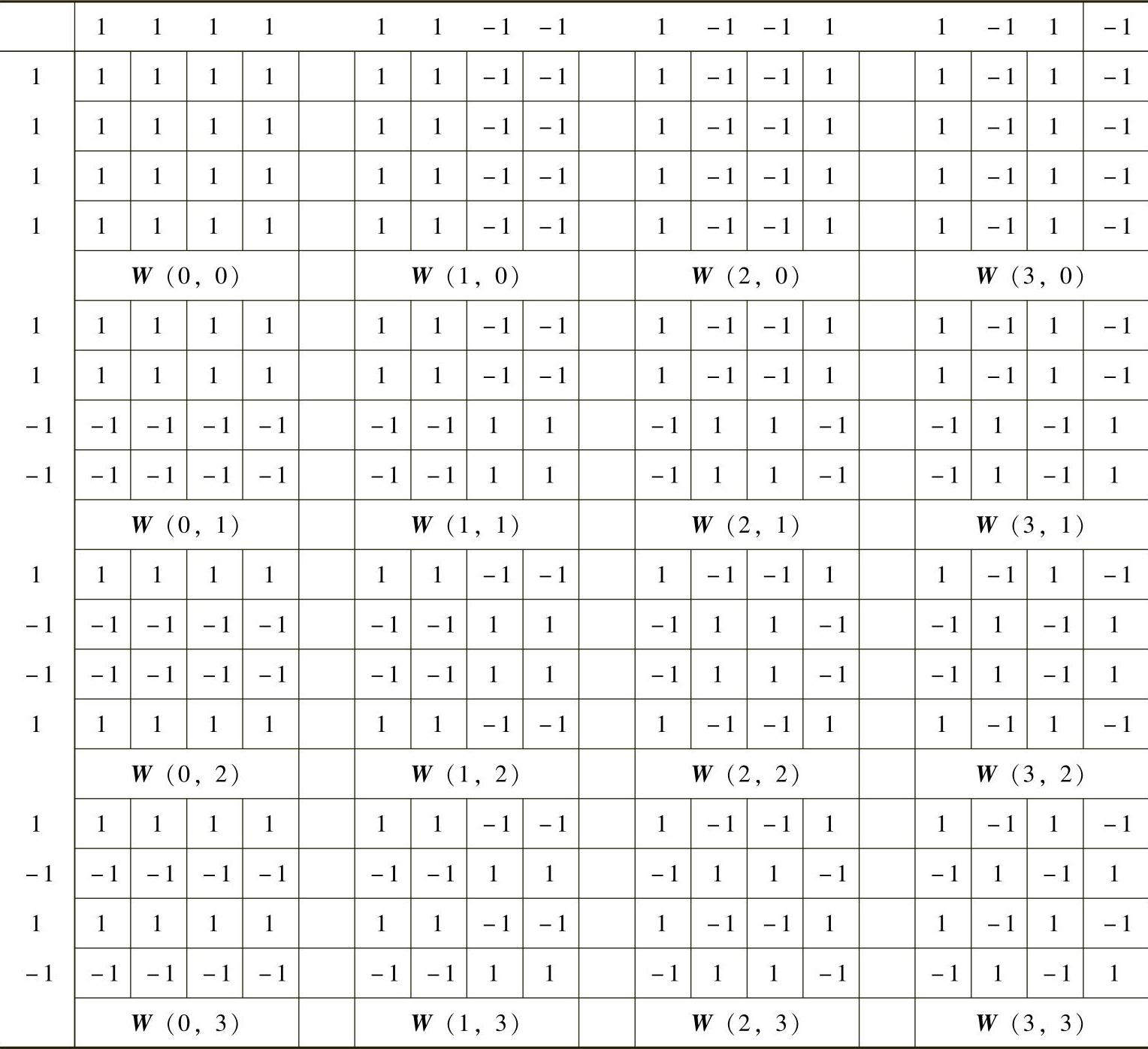
与傅里叶基本图像不同的是，沃尔什变换等其他正交变换基图像均是实矩阵。构造基本图像及其列率谱的MATLAB实现代码（只列出基矩阵生成过程）如下：

运行结果如图5-5所示。

图5-5 基本图像及列率谱

任意一幅N×N图像都可以分解成N²个基本图像加权和，权系数即为列率谱矩阵T_W对应元素值。二维沃尔什变换具有以下性质：

（1）线性

令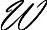{f（x，y）}表示离散函数f（x，y）的傅里叶变换，即T（u，v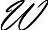）={f（x，y）}，则式（5-36）定义的傅里叶变换可得：

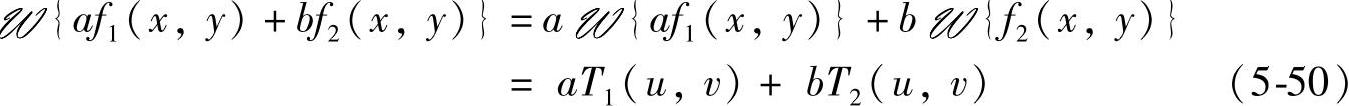
（2）列率搬移

两个二维沃尔什函数相乘为

Wal（k，m，x，y）·Wal（l，n，x，y）=Wal（kl，mn，x，y）（5-51）

（3）并元移位

如有原函数f（x，y），其沃尔什变换为F（k，m），自变量x、y做s、t位并元移位成为f（xs，yt）的沃尔什变换为F（k，m）s，t，则有以下关系成立：

F（k，m）s，t=F（k，m）·Wal（k，m，s，t）（5-52）

（4）循环并元卷积

信号的二维并元卷积的沃尔什变换等于信号沃尔什变换乘积，即

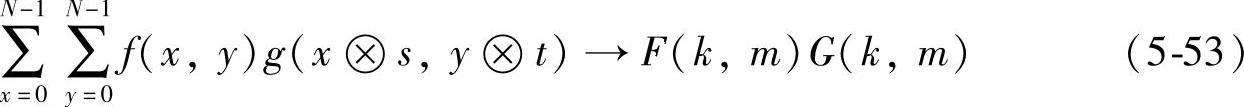
（5）调制性质

信号乘积的沃尔什变换等于信号沃尔什变换的并元卷积，即

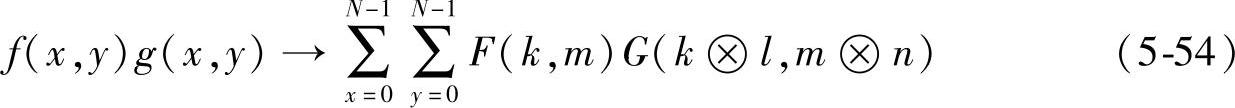
用MATLAB验证上述性质的代码如下：

二维哈达玛变换基矩阵与沃尔什基矩阵只是行向量排列顺序不同，正反变换形式相同。相应的，二维哈达玛变换基图像与沃尔什变换相同，只是顺序不同。