在三峡论证期间,确定了三峡工程采用五级船闸结合垂直升船机方案解决三峡枢纽通航。图5-87二维泥沙数学模型计算结果显示,三峡运用后期引航道口门段存在严重的淤积但是,将升船机和船闸同时包括在引航道内又导致船闸充水波动对升船机的影响和引航道内部泥沙淤积和清淤等问题。......
2025-09-29
图像表达的数学方式一般是二维矩阵,建立在矩阵表达上的图像处理同样可以在时域或变换域进行。同一维类似,基本系统分类如下。
1.线性系统和非线性系统
具有叠加性和齐次性的系统称为线性系统。假如系统的特性可表示成对输入图像进行H运算,并令f1(x,y)与Hf1(x,y)以及f2(x,y)与Hf2(x,y)分别代表两对输入与输出图像。当系统满足
H[f1(x,y)+f2(x,y)]=Hf1(x,y)+Hf2(x,y) (5-1)
关系时,称系统具有叠加性。当系统满足
H[kf(x,y)]=kHf(x,y) (5-2)
关系时,称系统具有齐次性。所以普遍来说,线性系统应满足以下关系:
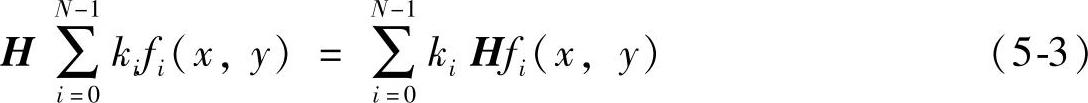
凡是不满足叠加性或齐次性的系统属于非线性系统。
2.位移不变系统与位移变化系统
位移不变系统的特性为:假设系统输入为f(x,y),所得输出Hf(x,y)记为g(x,y);那么当输入为f(x-x0,y-y0)时,对线性系统来说,其输出一般可表达成:
Hf(x-x0,y-y0)=g(x,x0,y,y0) (5-4)
它与(x,y)及(x0,y0)均有关系。对于位移不变系统来说,由于系统参数本身不随位置改变,因此系统的输出与输入的位置没有关系,故位移不变系统的特性可表示成:若Hf(x,y)=g(x,y),故有
Hf(x-x0,y-y0)=g(x-x0,y-y0) (5-5)
它表明当输入移动一个位置时,输出响应移动同样位置,但其形状不变。实际上,很多成像系统严格来说都是非线性的,但在一定条件下可看成线性的,且是位移不变的。本书中讨论的都是线性时不变系统模型。
从连续到数字转换的一个重要函数是冲激函数或δ函数,在二维情况下可写成:
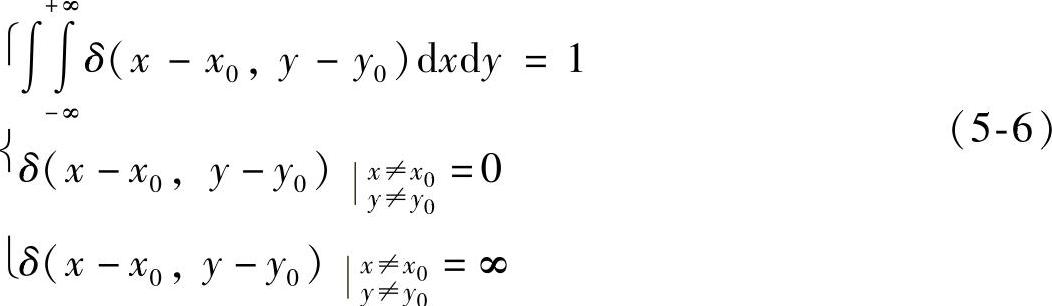
式(5-6)表示δ函数在出现(x=x0,y=y0)时为无限大,在其他各位置上其值为零,而它包含的体积是1。可用图5-2所示数学模型从直观上进行理解此广义函数。
在图5-2中,取中心在(x0,y0)点,面积为ε2的方块,有
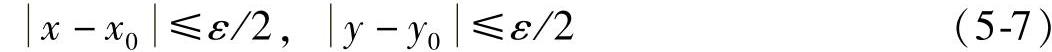
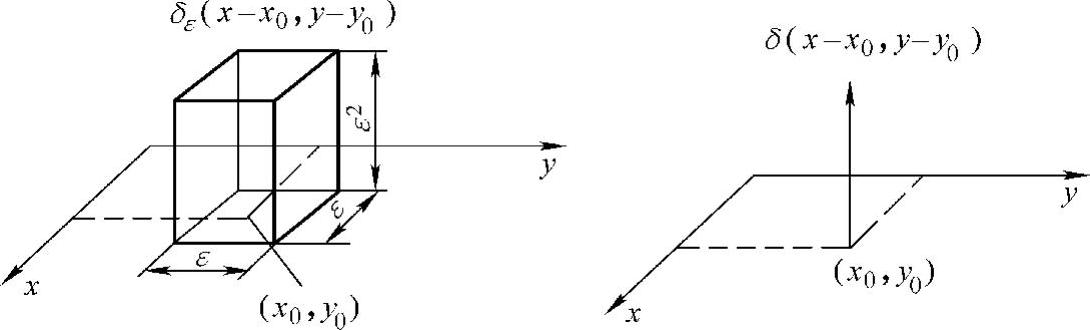
图5-2 方柱体与δ函数
并考虑在此方块内的一个方柱体冲激:

它在方块面积内取常数值1/ε2,在其他取值为零。由式(5-7)和式(5-8)可见,对任何ε值,方柱体冲激δε(x-x0,y-y0)所包含的体积均为1。当ε减少时,方柱体冲激的底面积变小,而其幅度增大。若使ε趋近于零,那么底面积ε2也趋近于零,而幅度1/ε2必趋近于无限大,但方柱体冲激所包含的体积仍然为1。这种极限的情况满足式(5-6)即δ函数,且其具有以下重要性质。
(1)筛选性质
考虑如下积分:
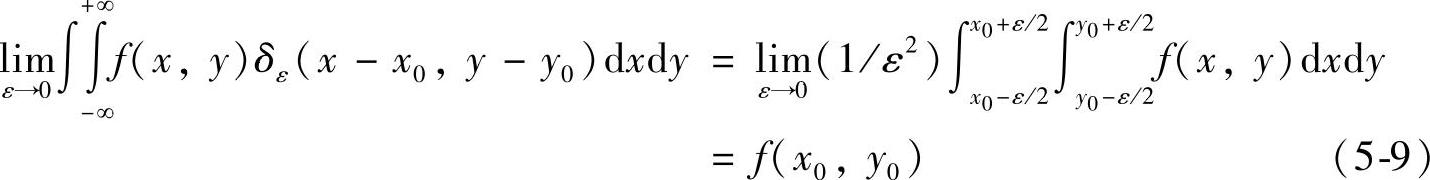
式(5-9)对包含(x0,y0)点的任一积分区域都正确。
(2)δ函数是偶函数
与上面的方法相同可得到:
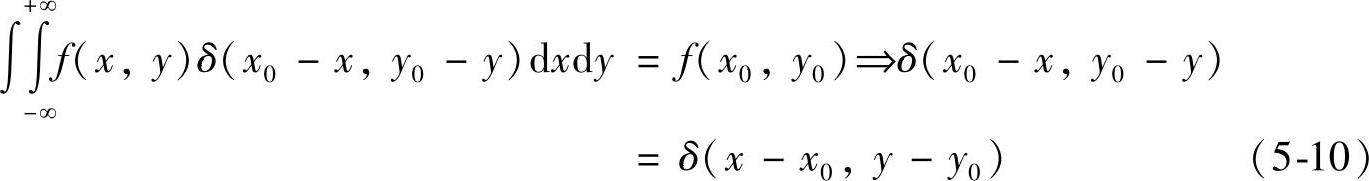 (https://www.chuimin.cn)
(https://www.chuimin.cn)
(3)卷积性质
根据式(5-9)和式(5-10)可得:
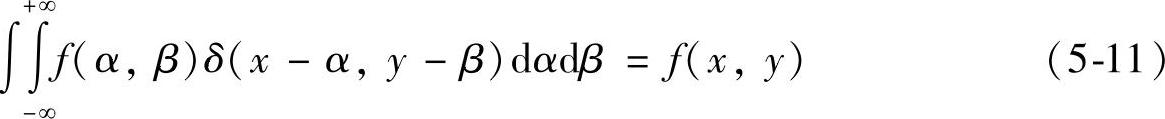
式(5-11)说明函数f(x,y)与δ(x,y)的卷积再次产生f(x,y),记作f(x,y)δ(x,y)=f(x,y)。并推广得到:
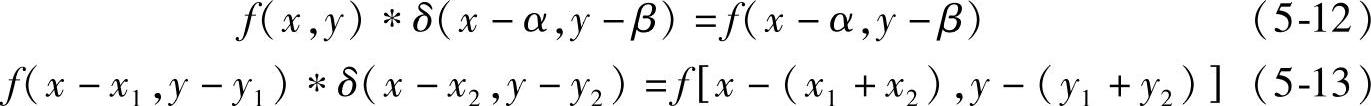
(4)可分离性质
δ(x-α,y-β)=δ(x-α)δ(y-β) (5-14)
尽管δ函数并不是普通意义上定义的函数。但它有着很强的物理背景。如一幅图像是由无限多个点所组成,每一个像素均可看做是点光源。所以,任意图像f(x,y)均可看做是无限多个点光源的组合。
根据卷积性质,若系统对输入图像就进行了线性运算H后将得到输出图像,结合线性系统叠加性和齐次性,可得如下表达式:
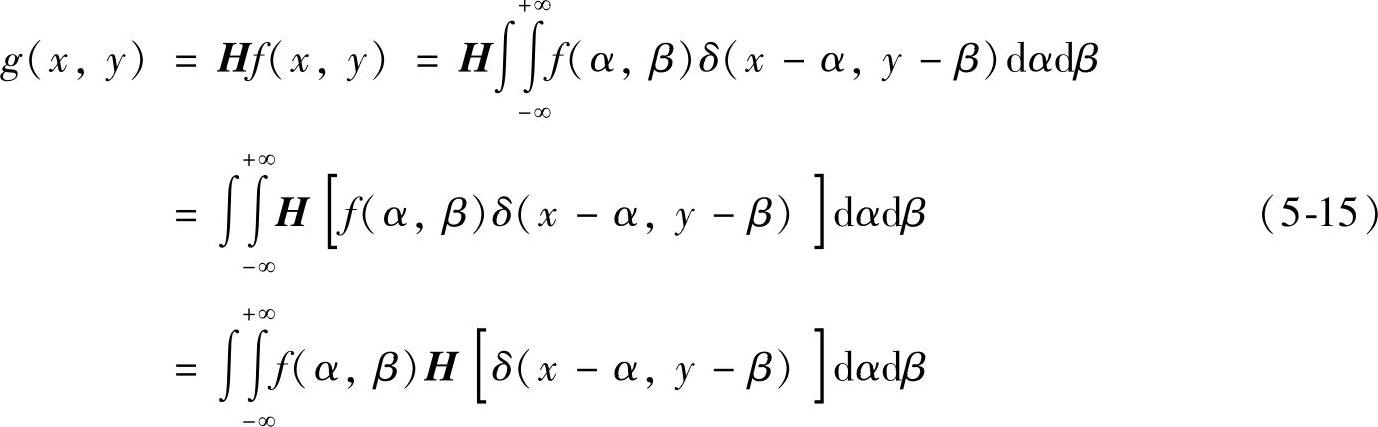
令
Hδ(x-α,y-β)=h((x,α;y,β) (5-16)
式中,h(x,α;y,β)称为系统单位冲激响应。将式(5-16)代入式(5-15)得
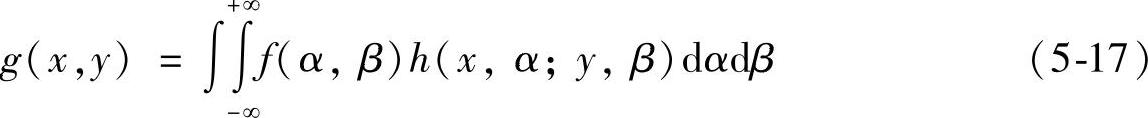
对于任意输入图像都可以按照式(5-17)计算得到输出图像即单位冲激响应完全表征了线性系统的特性。若系统是位移不变的,则系统输出与输入的位置无关,即
Hδ(x-α,y-β)=h(x-α,y-β) (5-18)
于是式(5-17)可简化成卷积形式:
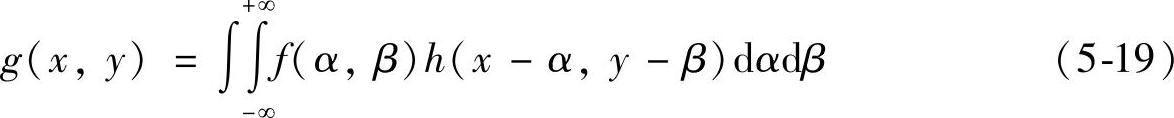
在图像处理中,通常是把成像系统描述成线性位移不变的,因为这种情况基本符合客观实际。系统能描述成线性位移不变具有很多优点,它可采用业已成熟的线性系统理论的许多手段进行分析,易于问题的数学处理。
式(5-19)给出了连续图像函数的卷积形式,用计算机实现时,仍然需要数字化后才能进行运算。假设对图像f(x,y)和系统冲激响应h(x,y)均匀取样,样本数分别为A×B和C×D,并在卷积前都周期性延拓成M×N样本,即
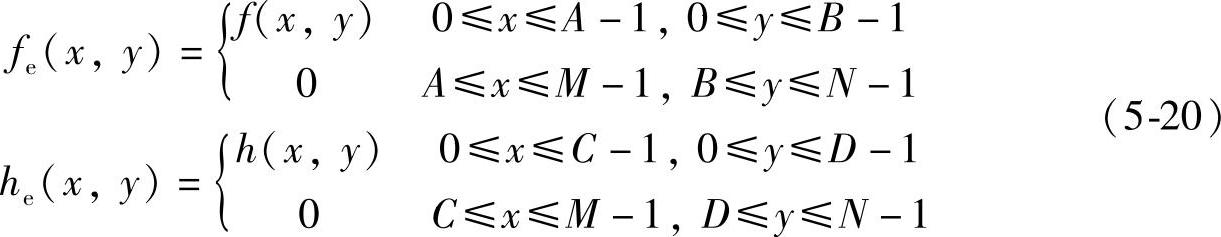
式中,fe(x,y)和he(x,y)都是二维周期性离散函数,在行列方向上的周期长度分别为M、N。这两个函数卷积等于:
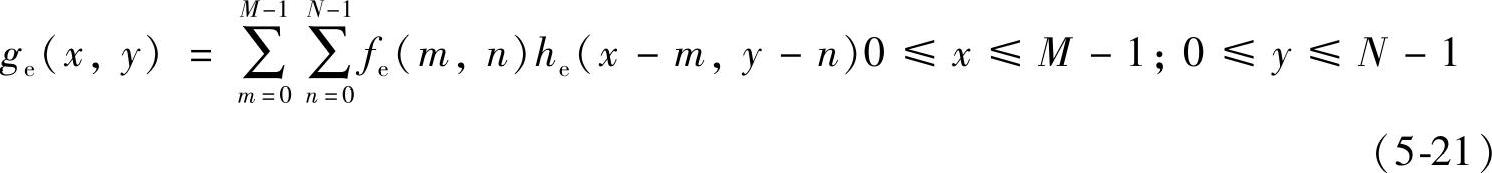
显然,ge(x,y)也是周期性离散函数,它在行列方向上的周期长度同样分别等于M、N。为使卷积不产生卷绕效应,必须选择M≥A+C-1和N≥B+D-1。
若含有M×N点阵的fe(x,y)和he(x,y)用列叠列的方法表示成MN维列向量,则式(5-21)可表示为
g=H·f (5-22)
式中,g及f是MN×1维列向量;H是MN×MN维方阵,包含M2个大小为N×N的分区,按分区排列的H方阵可写为
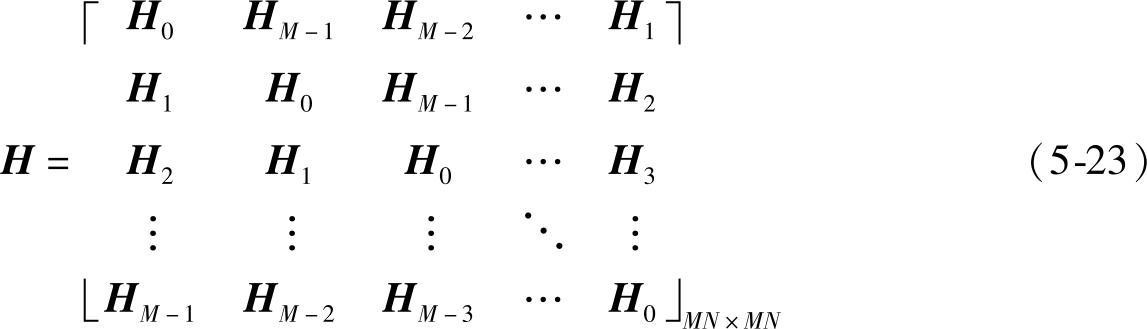
每一个分区Hj的元素是由h(x,y)的第j行扩展函数组成,即
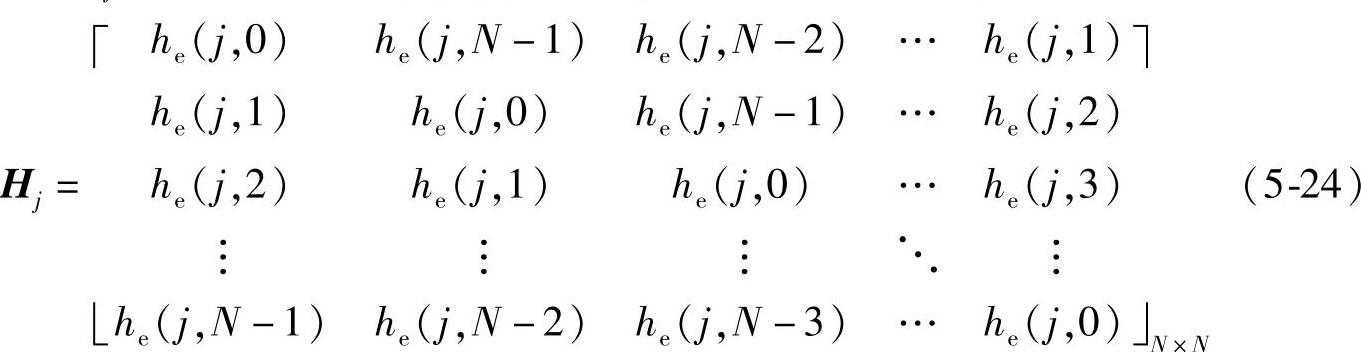
相关文章

在三峡论证期间,确定了三峡工程采用五级船闸结合垂直升船机方案解决三峡枢纽通航。图5-87二维泥沙数学模型计算结果显示,三峡运用后期引航道口门段存在严重的淤积但是,将升船机和船闸同时包括在引航道内又导致船闸充水波动对升船机的影响和引航道内部泥沙淤积和清淤等问题。......
2025-09-29

旗袍是中国传统服装文化的经典,它拥有浓厚的民族特点和丰富的艺术语言。旗袍的美主要体现在造型、色彩、纹样、材质等元素中。这种含蓄的曲线充分显示了女性自然的美,同时也非常符合东方女性的体型;其次,旗袍造型的变化,主要是襟形、袖式和领型等的变化。女性一般可针对自己的脸型、身材来挑选旗袍的襟形。图4-2-7如意襟旗袍图5.6TLM 电流分布示意图......
2025-09-29

实验采用对称的双断口结构,图6-25所示为实验模型的平面图及相关几何尺寸,单位均为mm。图6-25 气动斥力实验模型的平面图图6-26 气动斥力测试方法的原理图测量方法的原理如图6-26所示。下面的实验均是采用该方法进行的。图6-29 s=2mm,Im=4.2kA时的实验波形及电动斥力、气动斥力随时间的......
2025-09-29

二维码是采用某种特定的几何图形,按一定规律在平面分布的黑白相间图形记录数据符号信息的。图8-1二维码示意图1.部分1如图8-1中的3个回字,专业术语叫位置探测图形,对每个QR码来说,位置都是固定存在的,只是大小规格会有所差异;利用这些黑白间隔的矩形块,很容易进行图像处理的检测。......
2025-09-29

5.4.3.2杭州湾不恒定流及泥沙计算图5-73用平面二维泥沙数学模型计算三峡坝区泥沙浓度和泥沙淤积情况平面二维泥沙数学模型在计算三峡坝区泥沙浓度收敛过程 ;平面二维数学模型计算三峡坝区泥沙淤积时,比较沿程断面流量守恒情况图5-75杭州湾不恒定流水位、流速和泥沙浓度验证情况5.4.3.3葛洲坝三江上下游引航道的不恒定流验证图5-74杭州湾地理位置和计算区域示意图杭州湾位于钱塘江出海口,如图5-74所示,是一个强潮型河口。......
2025-09-29

电磁场中有电路和磁路的概念,热场中也有热路的概念。从这点上讲,把热场简化为热路,其精度比电磁场简化电路和磁路的要低,但通过适当处理也可满足工程计算要求。图5-2 电路与类比的热路a)电路 b)热路表5-1 热路参数与电路参数的类比利用以上热路和电路相似原理可对一具体开关电器建立其热路网络模型,求解热网络问题可采用电网络方法求解,例如用电网络的软件PSpice来计算。另一种求解热网络方法是热网络有限差分法。......
2025-09-29

由此可得动能和化学能共同作用下的开孔孔径dc图6.35活性聚能侵彻体作用混凝土靶开孔效应2.内爆超压模型活性聚能侵彻体贯穿混凝土靶后,在目标内部发生剧烈爆燃反应,形成超压场。图6.37靶后1 m处内爆超压时程曲线图6.38靶后2 m处内爆超压时程曲线活性聚能侵彻体等效TNT当量为100 g时,不同爆心位置处,靶后1 m和2 m处超压时程曲线分别如图6.39和图6.40所示。图6.41靶后超压时程曲线......
2025-09-29
相关推荐